
- •Расчет и конструкция двс
- •08.03.01 «Строительство»
- •Оглавление
- •Введение
- •1. Теория рабочих процессов, происходящих в двс
- •2. Силы действующие в кривошипно-шатунном механизме двс
- •3. Поршневая группа двс
- •4. Конструкция и принцип работы системы смазки двс
- •5 Практическая работа №1 «Теоретические циклы двс»
- •Контрольные вопросы
- •6. Практическая работа №2 Кинематика и динамика двс
- •7 Практическая работа №3 Расчет на прочность поршневой группы
- •8. Практическое занятие №4 Расчет системы смазки двс
- •Список литературы
- •Технические измерения
- •270100 «Строительство» по дисциплине
- •426069, Ижевск, ул. Студенческая, 7
2. Силы действующие в кривошипно-шатунном механизме двс
Расчет кинематики кривошипно-шатунного механизма
При изучении кинематики КШМ предполагают, что коленчатый вал двигателя вращается с постоянной угловой скоростью ω, отсутствуют зазоры в сопряженных деталях, и механизм рассматривают с одной степенью свободы.
В действительности из-за неравномерности крутящего момента двигателя угловая скорость переменна. Поэтому при рассмотрении специальных вопросов динамики, в частности крутильных колебаний системы коленчатого вала, необходимо учитывать изменение угловой скорости.
Независимой переменной принимают угол поворота кривошипа коленчатого вала φ. При кинематическом анализе устанавливают законы движения звеньев КШМ, и в первую очередь поршня и шатуна. За исходное принимают положение поршня в верхней мертвой точке (точка В1) (рис.4), а направление вращения коленчатого вала по часовой стрелке. При этом для выявления законов движения и аналитических зависимостей устанавливают.
наиболее характерные точки. Для центрального механизма такими точками являются ось поршневого пальца (точка В), совершающая вместе с поршнем возвратно-поступательное движение вдоль оси цилиндра, и ось шатунной шейки кривошипа (точка А), вращающаяся вокруг оси коленчатого вала О.
Для определения зависимостей кинематики КШМ введем следующие обозначения:
l – длина шатуна;
r – радиус кривошипа;

Рис 4 Схема кривошипно-шатунного механизма
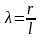 -
отношение радиуса кривошипа к длине
шатуна.
-
отношение радиуса кривошипа к длине
шатуна.
Для современных автомобильных и тракторных двигателей величина λ= 0.25–0.31.
Для высокооборотных двигателей с целью уменьшения сил инерции возвратно-поступательно движущихся масс, применяют более длинные шатуны, чем для малооборотных
β – угол между осями шатуна и цилиндра, величина которого определяется по следующей зависимости:
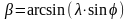
Наибольшие углы β для современных автомобильных и тракторных двигателей составляют 12–18°.
Перемещение (поршня
Перемещение (путь) поршня будет зависеть от угла поворота коленчатого вала и определяться отрезком Х (см. рис. 4) который равен
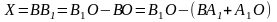
Из треугольников А1 АВ и ОА1А следует, что
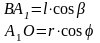
После преобразований получаем:
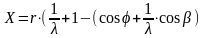 или
или
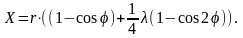
Полученное уравнение характеризует движение деталей КШМ в зависимости от угла поворота коленчатого вала и показывает, что путь поршня можно условно представить состоящим из двух гармонических перемещений:
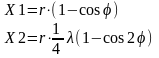
Где Х1 путь поршня первого порядка, который имел бы место при наличии шатуна бесконечной длины;
Х2– путь поршня второго порядка, т. е. дополнительное перемещение, зависящее от конечной длины шатуна.
На рис.5 даны кривые пути поршня по углу поворота коленчатого вала. Из рисунка видно, что при повороте коленчатого вала на угол, равный 90°, поршень проходит больше половины своего хода. Скорость поршня
Скорость поршня определяется как первая производная пути поршня по времени:
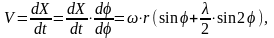
Скорость поршня можно представить в виде суммы двух слагаемых:
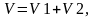
Где
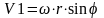 – гармонически
изменяющаяся скорость поршня первого
порядка, т. е. скорость, с которой двигался
бы поршень при наличии шатуна бесконечно
большой длины;
– гармонически
изменяющаяся скорость поршня первого
порядка, т. е. скорость, с которой двигался
бы поршень при наличии шатуна бесконечно
большой длины;
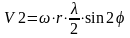 – гармонически
изменяющаяся скорость поршня второго
порядка, т. е. скорость дополнительного
перемещения, возникающая вследствие
наличия шатуна конечной длины.
– гармонически
изменяющаяся скорость поршня второго
порядка, т. е. скорость дополнительного
перемещения, возникающая вследствие
наличия шатуна конечной длины.

Рис.5. Изменение пути поршня в зависимости от угла поворота коленчатого вала
На рис. 6 даны кривые скорости поршня по углу поворота коленчатого вала. Значения углов поворота коленчатого вала, где поршень достигает максимальных значений скорости, зависят от λ и ее увеличением смещаются в стороны мертвых точек.
Для
практических оценок параметров двигателя
используется понятие средней скорости
поршня:
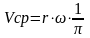 .
.
Для современных автомобильных двигателей Vср = 8–15 м/с, для тракторных – Vср = 5–9 м/с.
Ускорение поршня определяется как первая производная пути поршня по времени. Ускорение поршня можно представить в виде суммы двух слагаемых:

Рис 6 Изменение скорости поршня в зависимости от угла поворота коленчатого вала
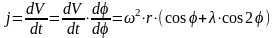
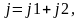
Где
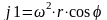 – гармонически
изменяющееся ускорение поршня первого
порядка;
– гармонически
изменяющееся ускорение поршня первого
порядка;
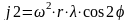 – гармонически
изменяющееся ускорение поршня второго
порядка.
– гармонически
изменяющееся ускорение поршня второго
порядка.
На рис. 7 даны кривые ускорения поршня по углу поворота коленчатого вала. Анализ показывает, что максимальное значение ускорения имеет место при нахождении поршня в ВМТ. При положении поршня в НМТ величина ускорения достигает минимального (наибольшего отрицательного) противоположного по знаку значения. Динамика кривошипно-шатунного механизма
Двигатели современных автомобилей и тракторов являются в большинстве случаев быстроходными, вследствие чего движущиеся детали их кривошипно-шатунного механизма перемещаются со значительными скоростями и ускорениями. В бензиновых двигателях

Рис 7. Изменение ускорения поршня в зависимости от угла поворота коленчатого вала
легковых автомобилей, например, ускорение поршня достигает 22000 м/с2, а величина средней скорости поршня – 16 м/с.
Поэтому для надежного расчета быстроходного двигателя изучение всех сил, действующих в нем, является крайне необходимым. Основные силы, действующие в автомобильных и тракторных двигателях, следующие:
силы давления газов, силы инерции, силы трения и силы сопротивления.
Силы инерции масс двигателя, которые движутся с переменными по величине и направлению скоростями, имеют место, как при холостом ходе, так и при работе его под нагрузкой, и для некоторых деталей двигателя являются основными расчетными силами.
В зависимости от характера движения силы инерции масс кривошипно-шатунного механизма можно распределить на три группы:
силы инерции возвратно-поступательно движущихся масс;
силы инерции вращающихся масс;
силы инерции масс, совершающих сложное движение.
Для определения величины этих сил необходимо предварительно найти величины соответствующих масс.
Приведение масс движущихся деталей кривошипно-шатунного механизма
Приведение массы шатуна
При динамическом исследовании двигателя обычно применяют приближенный способ определения сил инерции шатуна, заменяя на основании законов механики движение фактической массы шатуна движением двух или нескольких условных масс.
Для получения системы, динамически заменяющей действительную систему, необходимо соблюдение следующих условий:
Сумма всех заменяющих масс должна быть равна массе шатуна mш;
Общий центр тяжести всех заменяющих масс должен совпадать с центром тяжести шатуна и двигаться по закону движения этого центра тяжести;
Сумма моментов инерции всех заменяющих масс относительно оси, проходящей через центр тяжести шатуна, должна быть равна моменту инерции шатуна относительно той же оси Jш;
Угловое ускорение заменяющей системы во вращательном движении по отношению к ее центру тяжести должно быть равно угловому ускорению шатуна в том же движении.
Заменим массу шатуна тремя массами m1, m2, m3 (рис.8а), сосредоточенными в трех точках, лежащих на одной прямой, причем первая точка лежит на оси пальца поршня, точка В – на оси шатунной шейки коленчатого вала и точка D совпадает с центром тяжести шатуна.
Однако масса m3 по сравнению с массами m1 и m2 получается обычно незначительной, поэтому для упрощения динамических расчетов этой массой пренебрегают, заменяя массу шатуна двумя массами m1 и m2, расположенными в центрах его поршневой и кривошипной головок (рис.8 б). Такое пренебрежение приводит к небольшой ошибке, но очень упрощает расчет.
Условия приведения, необходимые для получения системы, эквивалентной в динамическом отношении системе шатуна, или условия динамического размещения массы, будут иметь вид:
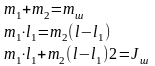


Рис 8 а,б Схема замены массы шатуна
Четвертое условие удовлетворяется, так как прямая, соединяющая центры масс m1 и m2, совпадает с осью шатуна.
Решая приведенные выше уравнения, получим:
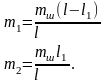
Масса m1 движется возвратно-поступательно вдоль оси цилиндра и поэтому относится к массе возвратно-поступательно движущихся частей; масса m2 совершает вращательное движение вокруг оси коленчатого вала и относится к массе вращающихся частей.
Для определения масс m1 и m2 необходимо знать вес шатуна mш, а также положение его центра тяжести. У готового шатуна эти величины определяют способами взвешивания и качаний. При проектировании в качестве первого приближения можно принять:
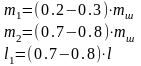
Величина mш определяется в соответствии с табл. в зависимости от площади поршня Fп (м2), диаметра цилиндра D, хода поршня S и типа двигателя. Меньшие величины mш следует брать для двигателей с S/D < 1.
Необходимо иметь в виду, что при расчетах на прочность стержня шатуна приведение масс не применяется, а учитывается действительное их размещение по длине шатуна.
Приведение вращающихся масс.
К вращающимся массам двигателя относятся: масса неуравновешенных частей коленчатого вала тк, часть массы шатуна m2,
Для удобства вычислений масса mк приводится к центру шатунной шейки. На рис. 6 представлена упрощенная схема одного колена вала. Неуравновешенной массой частей колена вала будет шатунная шейка с прилегающими к ней участками щек mшш и масса участков щек mщ, лежащих вне контура шатунной и коренной шеек с центром тяжести в точке О, который находится от оси коренной шейки.

Рис 9 Схема шатунной шейки коленчатого вала
Приведению подлежит только масса mщ,, т. к. центр ее тяжести не находится на расстоянии r от оси коленчатого вала. Согласно условию приведения при одинаковой угловой скорости ω вращения коленчатого вала центробежные силы приведенной тrщ и действительной тщ масс должны быть равны. Поэтому
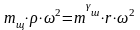
откуда приведенная неуравновешенная масса щеки коленчатого вала
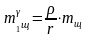
Тогда масса неуравновешенных частей коленчатого вала будет равна:
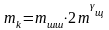 .
.
При выполнении проектных расчетов масса mк в качестве первого приближения принимается согласно данным табл. 1.1 Предварительные проектные размеры элементов коленчатого вала в табл. 1.2. масса mП в табл 1.3
Силы инерции кривошипно-шатунного механизма и силы давления газов
После приведения масс движущихся частей кривошипно-шатунного механизма к двум массам mr и mj силы инерции этих масс находят из условий их движения.
Силы инерции возвратно-поступательно движущихся масс вычисляют по формуле:
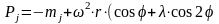
где
–
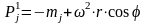 сила
инерции первого порядка; период изменения
этой силы – один оборот коленчатого
вала;
сила
инерции первого порядка; период изменения
этой силы – один оборот коленчатого
вала;
–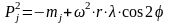 сила
инерции второго порядка; период изменения
этой силы – пол-оборота коленчатого
вала.
сила
инерции второго порядка; период изменения
этой силы – пол-оборота коленчатого
вала.
Эти силы действуют по оси цилиндра и считаются положительными, если они направлены к оси коленчатого вала, и отрицательными, если направлены от коленчатого вала (рис. 10).
Сила инерции вращающихся масс действует по радиусу кривошипа и определяется по формуле:
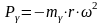
Силы давления газов в цилиндре двигателя в зависимости от хода
поршня определяют по индикаторной диаграмме, построенной по данным теплового расчета, или полученной экспериментально.
Сила
давления газов на поршень, действующая
по оси цилиндра, равна:
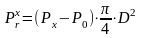
где PX – давление газов в цилиндре двигателя, P0 – давление в картере
D – площадь поршня.
Для динамического расчета двигателя, а также для расчета на прочность его деталей необходимо иметь зависимость PГ = f(φ) (рис.10) .
Сила PГ считается положительной, если она направлена к оси коленчатого вала.
Складывая алгебраически силы, действующие в направлении оси цилиндра, получим суммарную силу, действующую на КШМ, для каждой точки Х положения поршня
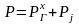
Диаграмма изменения этой силы по углу поворота коленчатого вала (для оборотов, соответствующих максимально эффективной мощности) представлена на рис. 10
Силы, действующие на поршневой палец, шатунные и коренные шейки
Разложим суммарную силу P, приложенную к оси поршневого пальца, на две составляющие силы (рис. 11а). Первая сила направлена по оси шатуна и равна:
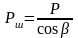
Графики сил PШ, N и Р по углу поворота коленчатого вала представлены на рис.11б
Перенесем силу Pш, действующую по оси шатуна, в центр шатунной шейки и затем разложим ее на две составляющие: касательную силу Т и перпендикулярную силу Z (рис 9).
Сила, действующая по оси кривошипа, равна:

Рис. 10. Графики сил PГ, Рj и Р по углу поворота коленчатого вала
Вторая сила перпендикулярна оси цилиндра и равна:
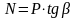
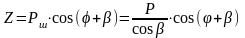
.

Рис. 11. Схема сил (а) и графики сил (б), действующих
на поршневой палец
Касательная сила определяется формулой:

Произведение силы Т на радиус r называют крутящим моментом двигателя:
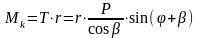
Графики сил T и Z по углу поворота коленчатого вала представлены на рис.12.
Кроме указанных выше сил на шатунную шейку действует, по радиусу кривошипа, сила инерции вращающихся масс Pr.
Приложим к центру коленчатого вала (точка О) (рис. 12) две взаимно противоположные силы Р'ш и Р''ш,, равные и параллельные силе Рш.
Силы Рш и Р''ш составят пару сил, момент которой на плече h равен:
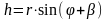 .
.

Рис. 12 Схема сил, действующих на коренной шейке
Тогда момент пары этих сил определяется формулой:
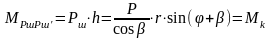 .
.
Он равен крутящему моменту двигателя Мк.
Разложим силу Р'ш на две составляющие силы:
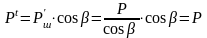 ,
,
.
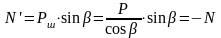
Сила Р' действует на опорную раму двигателя, силы же N и N' составят пару сил с плечом H, равным:
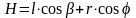
Тогда момент определяется формулой:
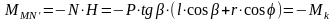 .
.
Он стремится опрокинуть двигатель и называется реактивным моментом двигателя.
Реактивный момент всегда равен крутящему моменту двигателя, но противоположен ему по направлению.
Выбор параметров деталей ДВС
Таблица 2.1 Выбор массы шатуна Мш, кг
Бензиновые двигатели D = 60–100 мм |
Дизели D = 80–130 мм |
(100–200) Fп |
(250–400)Fп |
Выбор массы неуравновешенной части одного колена вала
без противовесов mк ,кг
Бензиновые двигатели D = 60–100 мм |
Дизели D = 80–130 мм |
Стальной кованый вал (сплошные шатунные шейки) |
|
(150–200) Fп |
(200–400) Fп |
Стальной кованый и чугунный литой вал (полые шатунные шейки) |
|
(100–200)Fп |
(150–300) Fп |
Таблица 2.2 Выбор массы комплектного поршня mП, кг
Карбюраторные двигатели D=60–100 мм |
Дизели D=80–130 мм |
|
Поршень из алюминиевого сплава |
||
(80–100) Fп |
(150–300) Fп |
|
Чугунный поршень |
||
(150–250) Fп |
(250–400) Fп |
|
Таблица 2.3 Выбор размеров элементов коленчатого вала
Двигатели |
dш |
lш |
dк |
lк |
Бензиновые с однорядным расположением цилиндров |
(0.55–0.7)·D |
(0.45–0.7)·dш |
(0.65–0.8)·D |
(0.5–0.6)·dк |
Дизельные с однорядным расположением цилиндров |
(0.63–0.75)·D |
(0.73–1.0)·dш |
(0.72–0.9)·D |
(0.54–0.7)dк |
V-образные бензиновые с расположением двух шатунов на одной шейке |
(0.55–0.67)·D |
(0.8–1.0)·dш |
(0.62–0.7)·D |
(0.25–0.5)·dк |
V-образные дизельные с расположением двух шатунов на одной шейке |
(0.65–0.75)·D |
(0.95–1.05)·dш |
(0.68–0.76) ·D |
(0.5–0.6)·dк |
