Тема №10. Комплексные числа.
Расширенное понятие о числе. Мнимые и действительные числа.
Комплексные числа, действия с ними. Алгебраическая форма записи комплексного числа.
Геометрическое изображение комплексных чисел в декартовой системе координат. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа.
Формула Эйлера. Показательная форма комплексного числа.
Действия над комплексными числами в тригонометрической форме. Формулы Муавра.
Элементарные функции комплексного переменного.
Тема №11 Обыкновенные дифференциальные уравнения (ду).
Основные понятия ДУ: частное и общее решения, геометрический смысл решения ДУ I порядка, метод изоклин.
ДУ с разделяющимися переменными.
Однородные ДУ I порядка.
Линейные ДУ (ЛДУ) I порядка – два метода решения. ДУ Бернулли.
ДУ в полных дифференциалах.
ЛДУ высших порядков, основные свойства. Линейная зависимость и независимость решений ЛОДУ, определитель Вронского, общее решение ЛОДУ.
ЛОДУ с постоянными коэффициентами, характеристическое уравнение. Структура общего решения ЛОДУ в различных случаях корней характеристического уравнения.
Линейные неоднородные ДУ (ЛНДУ), структура общего решения, теорема о наложении решений. Подбор решений ЛНДУ по виду правой части.
Тема №12. Числовые и степенные ряды.
Числовой ряд – определение, частичные суммы, сумма ряда. Простейшие свойства сходящихся числовых рядов.
Необходимый признак сходимости ряда.
Признак Даламбера.
Интегральный признак сходимости рядов. Эталонный ряд
.Предельный признак сравнения рядов.
Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимости. Теорема Лейбница, её применение к оценке остатка ряда.
Функциональный ряд, область сходимости. Степенной ряд. Теорема Абеля. Дифференцирование и интегрирование степенных рядов.
Единственность разложения функций в степенной ряд. Ряды Тейлора (Маклорена). Разложение в ряд Маклорена функций е х, sinx,cosx,
.
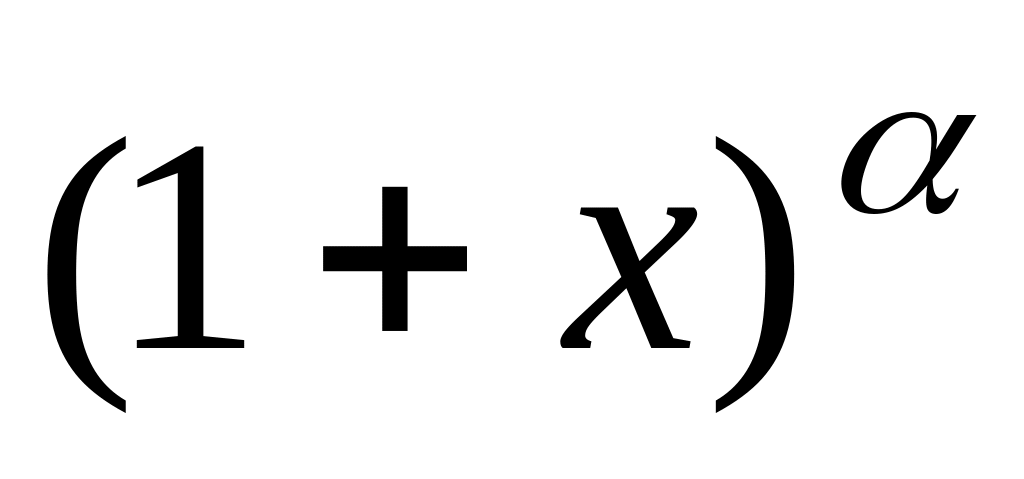Тема №13. Теория вероятностей.
Основные понятия теории вероятностей: случайное событие, пространство элементарных событий. Алгебра событий. Диаграммы Эйлера-Венна.
Вероятность случайного события. Аксиомы вероятностей, следствия из них, теорема сложения.
Примеры вероятных пространств – геометрические вероятности и классическое определение вероятности. Формулы комбинаторики.
Теорема умножения вероятностей.
Формула полной вероятности и формула Байеса.
Повторные испытания, формула Бернулли. Асимптотические формулы для формулы Бернулли: локальная теорема Муавра-Лапласа, интегральная теорема Лапласа, формула Пуассона.
Случайные величины (СВ), основные понятия. Ряд распределения и функция распределения дискретных СВ (ДСВ).
Функция распределения непрерывных СВ (НСВ). Общие свойства функции распределения.
Плотность вероятности и ее свойства.
Математическое ожидание СВ и его свойства.
Дисперсия СВ и ее свойства. Среднее квадратическое отклонение.
Примеры законов распределения; биноминальный закон, его свойства; закон Пуассона и его свойства; простейший поток событий.
Равномерное распределение и его свойства. Нормальное распределение и его свойства.
Предельные теоремы теории вероятностей. Лемма Маркова. Неравенство и теорема Чебышева. Неравенство и теорема Бернулли.
Понятие о центральной предельной теореме.