2. Понятие тела вращения. Цилиндр и его свойства. Сечения цилиндра плоскостью. Площадь поверхности и объем цилиндра.

Тело, образованное при вращении плоской ограниченной замкнутой фигуры вокруг прямой, лежащей в плоскости этой фигуры и не содержащей ее внутренних точек, называется телом вращения.

Тело, образованное при вращении прямоугольника вокруг прямой, содержащей его сторону, называется цилиндром.

К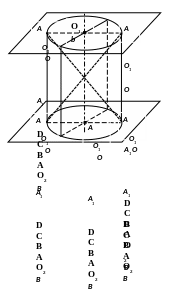 руги, образованные вращением сторон прямоугольника, перпендикулярных оси вращения, называются основаниями цилиндра и обозначается S_осн. Высотой цилиндра называется перпендикуляр, опущенный из любой точки одного основания на плоскость другого основания, а также длина этого перпендикуляра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный к их плоскостям, называется образующей цилиндра. Отрезок оси вращения, заключенный внутри цилиндра, называется осью цилиндра.

Если образующие цилиндра перпендикулярны плоскостям оснований, а в основании цилиндра круг, то такое тело называют прямым круговым цилиндром. Если основания прямого кругового цилиндра подвергнуть сжатию, получится эллиптический цилиндр. Если образующие цилиндра не перпендикулярны плоскостям оснований, то такое тело называют наклонным цилиндром.

Его основания – круги с центрами О₁ и О₂, а образующая АВ перпендикулярна плоскостям основа­ния.

Отрезок О₁А = О₂В – радиус основания.

Отрезок О₁О₂ – высота цилиндра, ось вращения.

Сечение ABCD – осевое сечение. Отрезок АС – диагональ осевого сечения. Точка F – центр симметрии фигуры.

Свойства цилиндра:

1. Основания цилиндра - равные круги.

2. Все сечения цилиндра плоскостями, параллельными плоскости основания, равны основаниям цилиндра и равны между собой.

3. Все сечения цилиндра плоскостями, не параллельными плоскости основания и пересекающими ось цилиндра, эллипсы или их части.

4. Все высоты цилиндра равны между собой и равны образующей.

5. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением цилиндра. Это прямоугольник, стороны которого равны диаметру основания и образующей. Все осевые сечения цилиндра равны между собой. Цилиндр, осевое сечение которого квадрат, называется равносторонним цилиндром.

6. Любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра.

7. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведенной через эту образующую, называется касательной плоскостью к цилиндру. Через каждую точку боковой поверхности цилиндра можно провести лишь одну касательную плоскость к цилиндру.

Разрежем боковую поверхность цилиндра по одной из его образующих и развернем. Получим прямоугольник с длиной, равной длине окружности основания 2R, и шириной, равной длине образующей или высоте цилиндра. Полученный прямоугольник называется разверткой боковой поверхности.

Если боковую поверхность цилиндра разрезать по одной из образующих, получится объединение плоских фигур – прямоугольника и двух кругов, называемое разверткой прямого кругового цилиндра.

Теорема о площади боковой поверхности цилиндра: Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

Площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона - высоте цилиндра.

Площадь основания цилиндра:

Площадь полной поверхности цилиндра:

Объем цилиндра: