Билет № 3.

1. Параллельные прямые в пространстве. Признак параллельности прямых.

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема (признак параллельности прямых). Если две прямые параллельны третьей прямой, то они параллельны.

Д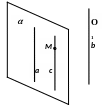 ано: Доказать:

Доказательство:

Случай, когда прямые а, b и с лежат в одной плоскости, рассмотрен в планиметрии. Рассмотрим случай, когда прямые а, b и с не лежат в одной плоскости.

Проведем плоскость  через прямую а и любую точку М, принадлежащую прямой с. Выясним, как расположена прямая с относительно плоскости . Так как прямая а лежит в плоскости  и параллельна прямой b, то прямая b не может пересекать плоскость . Следовательно, прямая с II b также не может пересекать плоскость . Получается, что прямая с не пересекает плоскость  и имеет с ней общую точку  прямая c  . Следовательно, прямые а и с лежат в одной плоскости . Они не могут пересекаться, так как в этом случае только одна из прямых а и с может быть параллельна прямой b. Следовательно,

Из теоремы следует, что из двух скрещивающихся прямых только одна может быть параллельна некоторой данной прямой.

2. Сечения конуса плоскостью. Объем усеченного конуса.

1. С ечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса. Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса. Все осевые сечения конуса - равные равнобедренные треугольники. ASB - угол при вершине осевого сечения конуса.

2. Любое сечение конуса плоскостью, параллельной плоскости осевого сечения конуса, также является треугольником, подобным треугольнику в осевом сечении.

3. Любое сечение конуса плоскостью, перпендикулярной оси конуса, является кругом меньшего по сравнению с основанием радиуса, причем центр этого круга лежит на оси конуса.

4. Любое сечение конуса плоскостью, проходящей через вершину конуса, но не проходящей через его ось, также является равнобедренным треугольником, образующим с плоскостью основания некоторый острый угол.

5. Любое сечение конуса плоскостью, не параллельной плоскости основания и не пересекающей основание, по форме является эллипсом, а в случае, когда плоскость пересекает плоскость основания, - частью эллипса. Поэтому эллипс называют коническим сечением.

6. Сечение, проходящее через ось симметрии конуса, делит его на два равных тела.

Т еорема о свойствах параллельных сечений конуса: Если конус пересечен плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части;