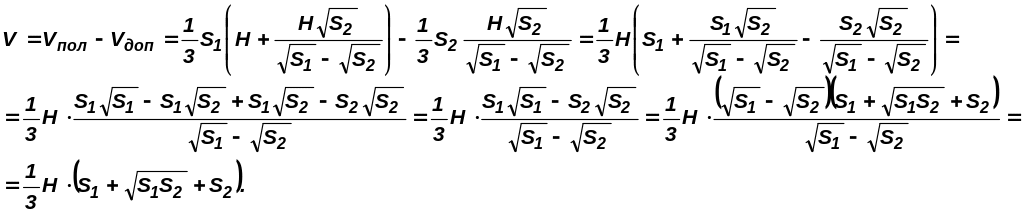Билет № 1.

1. Основные аксиомы стереометрии и следствия из них. Способы задания плоскости.

Раздел геометрии, в котором изучаются свойства фигур на плоскости (плоских фигур), называется планиметрией. Раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур), называется стереометрией. Слово «стереометрия» состоит из двух греческих слов «стереос» - телесный, пространственный и «метрео» - измеряю.

Основные фигуры в планиметрии: точка и прямая. Основные фигуры в стереометрии: точка, прямая, плоскость. Плоскость – это множество, элементами которого являются точки и в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямых. Плоскости обозначают строчными греческими буквами: , , … Пространство – это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.

Система аксиом стереометрии состоит из всех аксиом планиметрии и новой группы аксиом, в которых выражены свойства взаимного расположения точек прямых и плоскостей в пространстве.

А ксиома 1 (аксиома существования плоскости). В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии. Через любые три точки пространства, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Три точки, принадлежащие одной прямой, называются коллинеарными, а три точки, не принадлежащие одной прямой, называются неколлинеарными. Все точки одной прямой коллинеарны. Любые три неколлинеарные точки определяют плоскость. Плоскость, которая проходит через три точки А, В и С, не лежащие на одной прямой (САВ), обозначают символически АВС; если этой плоскостью является плоскость , то пишут  = АВС.

Аксиома 2 (аксиома принадлежности точек плоскости). Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

Аксиома 3 (аксиома принадлежности прямой плоскости). Если прямая проходит через две точки плоскости, то она лежит в этой плоскости.

И з аксиомы следует: (А, В)  АВ = m; m  . При этом говорят, что плоскость  проходит через прямую m (прямую АВ). В пространстве прямая может и не лежать в данной плоскости, но иметь с этой плоскостью ровно одну общую точку. В таком случае говорят, что прямая пересекает данную плоскость: а ∩  = {N}.

Определение: Прямая и плоскость, имеющие ровно одну общую точку, называются пересекающимися.

Аксиома 4 (аксиома пересечения плоскостей). Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

А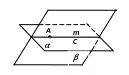 ксиома утверждает, что если две плоскости  и  имеют общую точку А, то они имеют и некоторую общую прямую m, которая проходит через точку А: Аm. Кроме того из аксиомы следует, что у плоскостей  и  нет общих точек вне их общей прямой m. В таком случае говорят, что плоскости  и  пересекаются по прямой m и записывают:  ∩  = {m}.

Определение: Две плоскости, имеющие общую точку, называются пересекающимися плоскостями.

А ксиома 5 (аксиома разбиения пространства плоскостью). Любая плоскость  разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что: а) любые две точки, принадлежащие разным множествам, разделены плоскостью ; б) любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью .

Рассмотрим плоскость . Она разбивает множество всех не принадлежащих ей точек пространства на два непустых множества P и Q, которые не имеют общих точек. Это разбиение обладает следующим свойством: если две точки (А и В) принадлежат одному и тому же множеству Р, то отрезок АВ не пересекает плоскость ; если же две точки (А и С) принадлежат разным множествам (АР, СQ), то отрезок АС пересекает плоскость . Это означает, что точки А и С разделены плоскостью .

Объединение множества Р и плоскости  (Р  ) называется полупространством, ограниченным плоскостью . Плоскость , ограничивающая это полупространство, называется его границей. Объединение множества Q и плоскости  (Q  ) также называется полупространством, ограниченным плоскостью . Пространство является объединением двух полупространств с общей границей – плоскостью .

А ксиома 6 (аксиома измерения расстояний). Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, проходящей через эти точки. Согласно аксиоме существования плоскостей в каждой плоскости выполняются аксиомы планиметрии. Следовательно, на каждой плоскости любым двум точкам ставится в соответствие положительное число – расстояние между ними на этой плоскости. Через точки А и В проходят одновременно две различные плоскости  и ; расстояние между точками А и В одно и то же для каждой из двух плоскостей. Расстояние между точками А и В обозначается символом АВ, либо (А, В), либо │AB │. При выбранной единице измерения расстояние между любыми двумя точками выражается положительным числом, которое показывает, сколько единиц измерения длин и частей этой единицы измерения содержится в данном расстоянии.

Теорема 1. Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

П усть даны прямая а и не принадлежащая ей точка А. Выберем на прямой а две любые точки В и С. Точка А не принадлежит прямой а, следовательно, точки А, В и С не лежат на одной прямой. Согласно аксиоме существования плоскостей через точки А, В и С можно провести единственную плоскость .

Прямая а имеет с плоскостью  две общие точки – В и С,  согласно аксиоме принадлежности прямой плоскости эта прямая лежит в плоскости .

Докажем, что другой плоскости, проходящей через точку А и прямую а (А  а), не существует. Предположим, что есть другая плоскость , проходящая через точку А и прямую а. Тогда плоскости  и  проходят через точки А, В и С, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость  – единственная.

Определение: Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку.

Теорема 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.

П усть прямые а и b пересекаются в точке С. Выберем на прямой а точку А, отличную от точки С (А  а, А ≠ С), а на прямой b точку В, отличную от точки С (В  b, В ≠ С). Тогда точка В не лежит на прямой а (В  а), следовательно, точки А, В и С не лежат на одной прямой. Согласно аксиоме существования плоскостей через точки А, В и С можно провести единственную плоскость .

Прямая а имеет с плоскостью  две общие точки – А и С,  согласно аксиоме принадлежности прямой плоскости эта прямая лежит в плоскости .

Прямая b имеет с плоскостью  две общие точки – B и С,  согласно аксиоме принадлежности прямой плоскости эта прямая лежит в плоскости .

Таким образом, плоскость  проходит через прямые а и b и является искомой.

Докажем единственность плоскости . Допустим, что есть другая плоскость , отличная от плоскости  и проходящая через прямые а и b. Так как плоскость  проходит через прямую а и не лежащую на ней точку В, то по теореме 1 она совпадает с плоскостью . Плоскость  – единственная.

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема 3. Через две параллельные прямые можно провести плоскость, и притом только одну.

П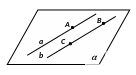 усть прямые а и b параллельны. Из определения параллельных прямых следует, что через прямые a и b можно провести плоскость. Обозначим ее  и докажем, что она единственна.

Допустим, что существует плоскость , отличная от плоскости  и содержащая каждую из прямых a и b. Выберем на прямой а точку А, а на прямой b – точки В и С. В силу параллельности прямых a и b точки А, В и С не лежат на одной прямой. Каждая из плоскостей  и  содержит обе прямые a и b, а значит, проходит через точки А, В и С. По аксиоме существования плоскости через эти три точки можно провести только одну плоскость. Следовательно, плоскости  и  совпадают.

Способы задания плоскости.

1. Тремя точками, не лежащими на одной прямой (по аксиоме существования плоскости).

2. Прямой и не принадлежащей ей точкой (по теореме 1).

3. Двумя пересекающимися прямыми (по теореме 2).

4. Двумя параллельными прямыми (по теореме 3).

2. Свойства параллельных сечений пирамиды. Усеченная пирамида.

Теорема о свойствах параллельных сечений пирамиды. Если пирамида пересечена плоскостью, параллельной основанию, то:

1) боковые ребра и высота делятся этой плоскостью на пропорциональные части;

2) в сечении получается многоугольник, подобный основанию;

3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Д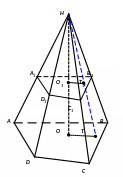 оказательство:

1. Пусть сечением пирамиды плоскостью, параллельной плоскости основания, является четырехугольник А₁В₁С₁D₁. Проведем высоту пирамиды НО, которая пересекает плоскость сечения А₁В₁С₁D₁ в точке О₁.

2. Проведем плоскость НАО. АО II А₁О₁ (по теореме о линиях пересечения параллельных плоскостей третьей плоскостью). ΔАНО  ΔА₁НО₁ (по следствию из первого признака подобия).  Аналогично доказывается отношение отрезков

3. Пусть плоскость АНВ пересекает плоскость сечения по прямой А₁В₁ и плоскость основания - по прямой АВ, тогда по теореме о линиях пересечения параллельных плоскостей третьей плоскостью А₁В₁ II АВ. ΔАНB  ΔА₁НB₁ (по следствию из первого признака подобия).  Аналогично доказывается отношение отрезков Стороны многоугольников пропорциональны.

4. Углы многоугольников ABCD и А₁В₁С₁D₁ попарно равны как углы с сонаправленными сторонами. Так как соответственные углы попарно равны, а сходственные стороны пропорциональны, то многоугольники ABCD и А₁В₁С₁D₁ подобны.

5. По теореме о площадях подобных многоугольников

Следствие. Плоскость, параллельная основанию пирамиды, отсекает от нее пирамиду, подобную данной.

Многогранник АВСDА₁В₁С₁D₁ называется усеченной пирамидой. Грани АВСD и А₁В₁С₁D₁, лежащие в параллельных плоскостях, называются соответственно нижним и верхним основаниями усеченной пирамиды, остальные грани - боковыми гранями усеченной пирамиды. Так как верхнее и нижнее основание лежат в параллельных плоскостях, то боковые грани - трапеции.

Усеченной пирамидой называется часть полной пирамиды, заключенная между ее основанием и параллельным ему сечением.

Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Усеченная пирамида называется правильной, если она получена из правильной пирамиды. Из определения следует, что основания правильной усеченной пирамиды - подобные правильные многоугольники, а боковые грани - равные равнобедренные трапеции. Высоты этих трапеций называются апофемами усеченной пирамиды.

Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.

Теорема о площади боковой поверхности правильной усеченной пирамиды. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований на апофему.

Доказательство:

Теорема об объеме усеченной пирамиды. Объем усеченной пирамиды, у которой площади оснований равны S₁ и S₂, а высота - Н, вычисляется по формуле:

Доказательство:

Дополним усеченную пирамиду до полной. Тогда объем усеченной пирамиды равен разности объемов полной и дополнительной пирамид.

По свойству параллельных сечений