20. Численный метод решения уравнений состояния динамической цепи.

Простейший метод численного интегрирования, с помощью которого можно рассчитать уравнения переменного состояния является метод Эйлера (метод ломанных). При его использовании задаются начальные условия, а их последующие значения вычисляются шаг за шагом с помощью рекуррентного соотношения

- рекурсия.

Приращение переменной ΔХ можно получить уз уравнения состоянии, заменив их уравнения в конечных приращениях.

Из уравнений в конечных приращениях определяется приращение переменных состояния на текущем этапе расчета и их значение в конце шага.

Записанные уравнения отражают алгоритм метода Эйлера для решения дифференциальных уравнений.

III. Периодические несинусоидальные токи в электрических цепях.

1. Основные понятия о несинусоидальных эдс, напряжениях, тока и методах анализа.

Для большинства эл.приёмников нормальный режим работы обеспечивается подачей синусоидального напряжения. Устанавлены нормы допустимого отклонения периодических ЭДС, напряжения и тока от синусоидальной формы.

В реальных условиях в эл.установках различного назначения возникать несинусоидальные токи. Например включение в цепь нелинейных элементов.

В реальных эл.цепях функции описывающие несинусоидальные ЭДС, напряжение, токи всегда удовлетворяют условиям Дирихле, то есть за полный период имеют конечное число разрывов 1-го рода и конечное число максимумов и минимумов. Такую функцию можно разложить в гармонический ряд Фурье. Представив периодические несинусоидальные ЭДС, напряжение или ток в виде суммы бесконечного числа синусоидальных ЭДС, напряжения или токов различной частоты, можно свести изучение процесса в цепях с несинусоидальными величинами к изучению процессов в цепях с синусоидальными величинами.

При разложении в ряд Фурье периодическая несинусоидальная ЭДС имеет вид:

, -Значение несинусоидальной ЭДС в момент времени t,

Е₀-постояная составляющая ЭДС.

-Основная или 1-я гармоника, имеющая ту же частоту, что и несинусоидальная ЭДС

-Гармоника высшего порядка, имеющая частоту в К раз больше основной.

-Амплитуды гармоник 1-го, 2-го, К-го порядка, -угловая частота основной гармоники..

-начальные фазы гармоник.

Для определения амплитуд гармоник целесообразнее её представить в виде суммы 2-х гармоник =0 ;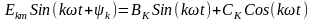

Амплитуды гармонических составляющих (коэффициенты В_К и С_К) зависят от начальные фаз и поэтому изменяются при изменении начала отсчёта времени.

; ;

Для ограниченного числа членов ряда:

;

; ; ;

; .

2. Действующие и средние значения несинусоидальных электрических величин.

Действующие значение несинусоидальных ЭДС (напряжения и тока), равно среднеквадратичному её значению за время равное её периоду:

;

- мгновенное значение несинусоидальной ЭДС;

- К-ая гармоника ;

Действующее значение несинусоидальной ЭДС:

Аналогично для действующихх значений тока и напряжения:

; _;

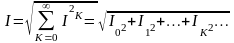Действующее значение несинусоидальной величины равно корню квадратному из суммы квадратов действующего значения и действующих значений её гармоник(просто прочитать).

Для упрощения расчетов при отсутствии постоянных составляющих несинусоидальную величину заменяют эквивалентной синусоидальной (такая величина, действующее значения которой равно действующему значению несинусоидальной величины).

Амплитуда эквивалентной синусоидальной ЭДС:

;

Среднее значение за полупериод: .