2. Переходные процессы в цепи с последовательным соединением элементов с r и l при подключении ее к источнику постоянного напряжения

Все катушки и обмотки эл. аппаратов и машин имеют сопротивления R и индуктивность L.

В начальный момент времени тока в цепи нет, тогда:

=0

После подключения цепи к источнику постоянного напряжения в установившемся режиме существует некоторый ток

≠0, W_М>0

Следовательно, в то время, когда происходит изменение энергии магнитного поля индуктивной катушки от 0 до некоторого значения, в цепи имеет место переходный процесс и существует переменный ток (t).

По 2 закону Кирхгофа:

Ток

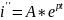
Для нахождения p составим характеристическое уравнение.

Ток переходного процесса:

Постоянную интегрирования определяем с учетом первого закона коммутации из начальных условий.

i_L(0-)=i_L(0+)=0

Величина имеет размерность времени. . Ее называют постоянной времени цепи, характеризует скорость протекания ПП. Зависит от L, R.

Свободный ток при t=0 равен по значению установившемуся току, но имеет обратное направление. Общий ток в цепи изменяется от 0 до установившегося значения по экспоненциальному закону.

равна такому промежутку времени, в течение которого свободный ток уменьшается в раз.

Падение напряжения на резисторе изменяется по такому же закону что и ток

3. Переходные процессы в цепи при зарядке и разрядке.

S- двухполюсный выключатель

1. когда зарядка

2. отсекается источник напряжения и разрядка

S в положение 1, в момент включения (конд разряжен). Чтобы зарядить конд до напряжения U, ему надо сообщить заряд Q=CU.

Процесс зарядки растянут во времени и напряжение на конд-ре нарастает постепенно.

По 2ому закону Кирхгофа:

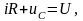
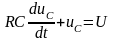(линейное неоднородное уравнение 1ого порядка)

-свободное напряжение находят решая однородное диф уравнение.

, р-корень характеристического уравнения

Составим характеристическое уравнение: RCP+1=0? ,

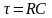-постоянная времени цепи

Напряжение на конд-ре в переходном режиме:

Постоянную А находят с учетом 2ого закона коммутации из начальных условий работы цепи, которые различны для процессов зарядки и разрядки.

ЗАРЯДКА КОНДЕНСАТОРА.

, , , (ток через конденсатор не течет)

, следовательно, напряжение в переходном режиме при зарядке конд-ра изменяется по закону

-характеризует скорость зарядки конденсатора

При t=0 (начальный процесс зарядки) ток i в цепм ограничен только сопротивлением и при малом значении R может достигать больших значений. .

РАЗРЯДКА КОНДЕНСАТОРА.

Переключатель S включается в положение 2. Конд-тор заряженный до напряжения U начинает разряжаться через резистор R(энергия рассеивается в окружающую среду на активном сопротивлении).

A=U, , ,

Скорость разрядки определяется . Физический смысл :

Постоянная времени- это промежуток времени в течении которого конденсатор полностью зарядился или разрядился бы, если бы ток зарядки или разрядки оставался постоянным и равным начальному значению.