VI. Магнитные цепи.

1. Магнитные цепи при постоянных магнитных потоках.

Магнитная цепь- совокупность ферромагнитных тел и воздушных сред, по которым замыкается магнитный поток. (сердечник тр-ра, магнитопровод сварочного тр-ра, магнитопровод катушки реле и т.д.)

Магнитные цепи являются частью электротехнического устройства и предназначены для создания в заданном объеме магнитного поля нужной интенсивности.

В неразветвленных магнитных цепях поток сечений каждого участка один и тот же.

2. Закон Ома и законы Кирхгофа для магнитных цепей.

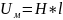,- магнитное напряжение, , – индукция

,

Закон Ома: Магнитное напряжение на участке цепи равно произведению потока на магнитное сопротивление.

-закон Ома для магнитной цепи,

- магнитное сопротивление, нелинейная величина, поэтому осложняет применение з. Ома и 2ого закона Кирхгофа.

, * гнитная постоянная

В замкнутом контуре: Ф= ; .

1 закон Кирхгофа вытекает из принципа непрерывности линий магнитной индукции: В любом узле сложной магнитной цепи алгебраическая сумма магнитных потоков равна 0.

Магнитные потоки направленные к узлу берут со знаком “+”, а выходящие из узла со знаком “-”.

2 закон Кирхгофа: В любом замкнутом контуре сложной магнитной цепи алгебраическая сумма магнитных U равна сумме МДС действующих в этом контуре.

или

Электрическая цепь	Магнитная цепь
Действует ЭДС, Е. ЭДС вызывает ток. U=IR, R имеет ВАХ. 1 закон Кирхгофа ∑I=0. 2 закон Кирхгофа ∑U=0.	Действует МДС, F=Iw МДС вызывает поток ; имеет вебер-амперную хар-ку

Данная аналогия приводит к выводу о возможности использования схем замещения для магнитных цепей постоянного магнитного потока в виде графического изображения элементов магнитной цепи подобных элементам электрической цепи.

3.Расчет неразветвленных магнитных цепей.

При расчете необходимо знать 3 основных соотношения, при этом считая, что магнитное поле однородное.

1. Ф=BS, 2. , 3.

Кроме того нужно знать кривую намагничивания ферромагнитного сердечника. B=B(H)

Цепь состоит из магнитопровода 1 с воздушным зазором 2 и намагничивающей обмотки 3. Считается, что в такой цепи магнитный поток одинаков во всех сечениях, т.е. пренебрегает потоками рассеивания.

Сечение воздушного зазора сечения магнитопровода. Из-за явления выпучивания магнитных силовых линий.

Площадь зазора определяется поперечным размером ab.

В большинстве практических задач считают .

При расчете неразветвленных магнитных цепей различают прямую и обратную задачи.

• В прямой задаче задается значение Ф или В в зазоре, геометрические размеры магнитной цепи( , , ). Найти МДС. Порядок решения:

1. по находим поток Ф= , Вб.

2. , Тл.

3. по кривой намагничивания материала сердечника для полученного значения В1 находят напряженность магнитного поля Н1 в сердечнике.(А/м)

4. Напряженность в зазоре: =

5. Iw= , Iw ( в зазоре много больше, чем в стали, и в основном МДС расходуется на преодоление сопротивления воздушного зазора).

• Обратная задача: заключается в том, что задают Iw=F. Нужно определить индукцию в зазоре В₀.

Решение: задаются несколькими произвольными значениями магн. индукции в зазоре и определяют для них МДС. Строят зависимость Iw_К=f(B_0k).

По зависимости определяют какая В₀.

Используя закон Ома: Магнитное сопротивление всей цепи равно сумме магнитных сопротивлений ее последовательно соединенных участков: Iw=

Схема замещения магнитной цепи:

По закону Ома: Ф=

Поскольку величина не линейная и зависит от величины В, то решение находятся методом последовательных приближений. Этот процесс заканчивают при достижении заданной точности расчета.

Графоаналитический метод:

,

Строим 2 вебер-амперные характеристики.

Для построения этих функций рассчитывается ряд значений для параметров исходной магнитной цепи.

Значение Н₁ определяем по кривой В=В(Н), для заданного материала сердечника.

,строим график. Ф=Ф₀. Определяем U_м1 и U_м0. Находим