I. Четырехполюсники.

1. Основные определения и классификация четырехполюсников.

Четырехполюсник — это обобщенное наименование электрической цепи, рассматриваемой по от­ношению к четырем ее зажимам.

Трансформатор, линию передачи энергии, мостовую схему и т. п. мож­но рассматривать как четырехполюсники.

Принято изображать четырехполюсник в виде прямоугольника с выходящими из него концами (полюсами). Если че­тырехполюсник содержит источники электрической энергии, то в прямо­угольнике ставят букву А (активный); если буква А отсутствует, то это значит, что четырехполюсник пассивный.

Входной ток обозначают входное напряжение— ; ток и напря­жение на выходе — и .

Четырехполюсник является передаточным звеном между источником питания и нагрузкой. К входным зажимам тп, как правило, присоединя­ют источник питания, к выходным зажимам pq — нагрузку.

Предполагается, что нагрузка четырехполюсника и напряжение на входе при работе четырехполюсника в качестве связующего звена могут изменяться, но схема внутренних соединений четырехполюсника и со­противления в ней остаются неизменными.

Классификация четырехполюсников:

1. Линейные и нелинейные (ВАХ элементов четырехполюсника)

2. Пассивные и активные (наличие ЭДС)

3. С сосредоточенными параметрами и распределенными параметрами.

4. Симметричные и не симметричные (A=D, A≠D)

5. Эквивалентные и не эквивалентные.

2. Системы уравнений четырехполюсников.

Четырехполюсник характеризуется двумя напряжениями и и двумя тока­ми и . Любые две величины можно определить через остальные (I₁ U₁ через I₂ U₂).

Существует 6 форм записи уравнений четырехполюсника:

A–форма:

Y-форма:

Z-форма:

H-форма:

G-форма:

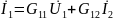
B-форма:

Существует попарная инверсия Y и Z форм, А и В форм, Н и G форм.

Для основной А формы положительные направления для токов и напряжений соответствуют рис. 1, для Y, Z, H, G форм — рис. 2, для B формы — рис. 3.

3. Входное сопротивление четырехполюсника при произвольной нагрузке.

Комплексные входные сопротивления находят опытным путем с помощью ваттметра, амперметра и вольтметра.

Определим комплексное входное сопротивление ч-ка, при 3х различных режимах его работы.

1. При питании со стороны зажимов m,n и разомкнутой ветви p,q.

2. При питании со стороны зажимов m,n и КЗ ветви p,q

3. При питании со стороны p,q и КЗ зажимов m,n

Комплексные коэффициенты A,B,C,D зависят от схемы внутренних соединений ч-ка, значений сопротивлений схемы и частоты. Для каждого ч-ка их можно определить расчетным или опытным путем. Для ч-ков, удовлетворяющих условию взаимности, коэффициенты связаны соотношением:

4. Соединения четырехполюсника.

Функции пассивного взаимного четырехполюсника как передаточного звена между источником питания и нагрузкой может выполнять T схема (соединение звездой) или эквивалентная ей П схема (треугольником).

Предполагается, что частота ω фиксирована, ω=сonst.

Три сопротивления Т или П схемы подсчитывают с учетом того, что схема замещения должна обладать теми же коэффициентами A,B,C,D, что и заменяемый ею четырехполюсник.

Для Т-схемы.

, , ,

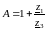Через A,B,C,D можем определить z₁,z₂,z_3.

, ,

Аналогичным образом находятся параметры П - схемы замещения.

A=D – в симметричном четырехполюснике.

в Т – схеме замещения z₁=z₂.

в П -схеме Z₅=z₆