
- •Львівська комерційна академія
- •Видавництво Львівської комерційної академії
- •Навчальна програма дисципліни
- •Тема 1. Основні поняття теорії ймовірностей
- •Тема 2. Залежні й незалежні випадкові події.
- •Тема 3. Спроби за схемою бернуллі
- •Тема 4. Одновимірні випадкові величини
- •Тема 5. Багатовимірні випадкові величини
- •Тема 11. Елементи математичної статистики. Вибірковий метод
- •Тема 12. Статистичні оцінки параметрів генеральної сукупності. Статистичні гіпотези
- •Тема 13. Елементи дисперсійного аналізу
- •Тема 14. Елементи теорії регресії і кореляції
- •Список рекомендованої літератури
- •Правила виконання контрольної роботи
- •Завдання для контрольної роботи Тестові завдання
- •Практичні задачі Завдання 1. Класичне та геометричне визначення ймовірності
- •Завдання 2. Формула повної ймовірності. Формули Байєса
- •Завдання 3. Схема Бернуллі. Формула Бернуллі
- •Завдання 4. Граничні теореми у схемі Бернуллі
- •Завдання 5. Дискретні випадкові величини
- •Завдання 6. Неперервні випадкові величини
- •Завдання 7. Вибірки з дискретно розподіленими ознаками та їх характеристики. Точкові оцінки параметрів дискретно розподілених ознак генеральної сукупності
- •Завдання 8. Перевірка гіпотез про нормальність розподілу генеральної сукупності
- •Завдання 9. Елементи кореляційно-регресійного аналізу
- •Розв’язування типових завдань Класичне та геометричне означення ймовірності
- •Формула повної ймовірності. Формули Байєса
- •Дискретні випадкові величини
- •Неперервні випадкові величини
- •Математична статистика
- •Додаток
- •Значення функції
- •Значення функції Лапласа
Правила виконання контрольної роботи
Контрольна робота виконується студентами в аудиторії під час заліково-екзаменаційної сесії.
Завдання складаються з 10 тестових завдань та 9 практичних задач і видаються викладачем індивідуально кожному студентові.
Кожне тестове завдання оцінюється в 1 бал, задача — 3 бали.
Контрольна робота зараховується, якщо студент набирає більше 22 балів.
Завдання для контрольної роботи Тестові завдання
Кількість перестановок на множині з
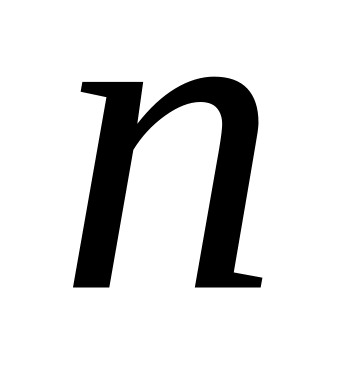 елементів визначається
за формулою:
елементів визначається
за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
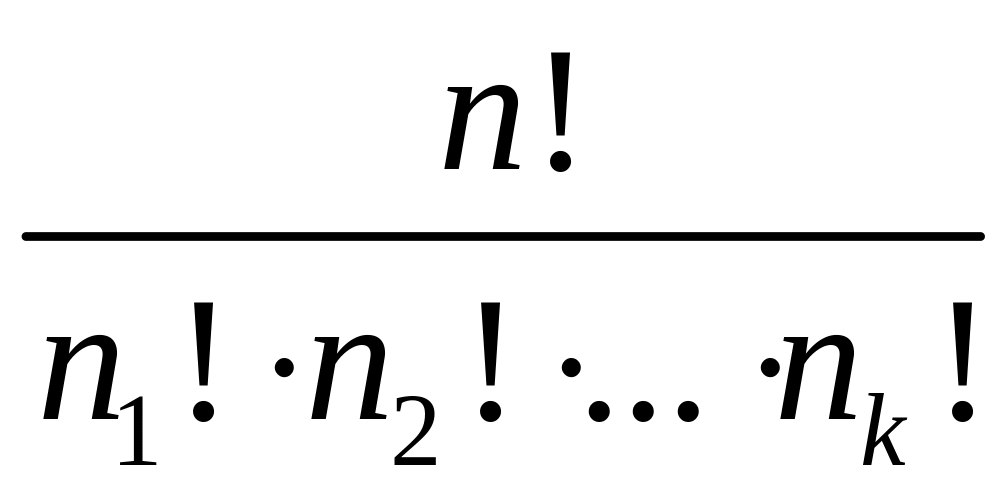 .
.
Перестановкою на множині з елементів називається:
а) довільна -елементна підмножина цієї множини;
б)
впорядкована
![]() -елементна
-елементна
![]() підмножина цієї множини;
підмножина цієї множини;
в) довільна впорядкована -елементна підмножина цієї множини.
Кількість розміщень з елементів по визначається за формулою:
а)
![]() ;
б)
;
б)
 ;
в)
;
в)
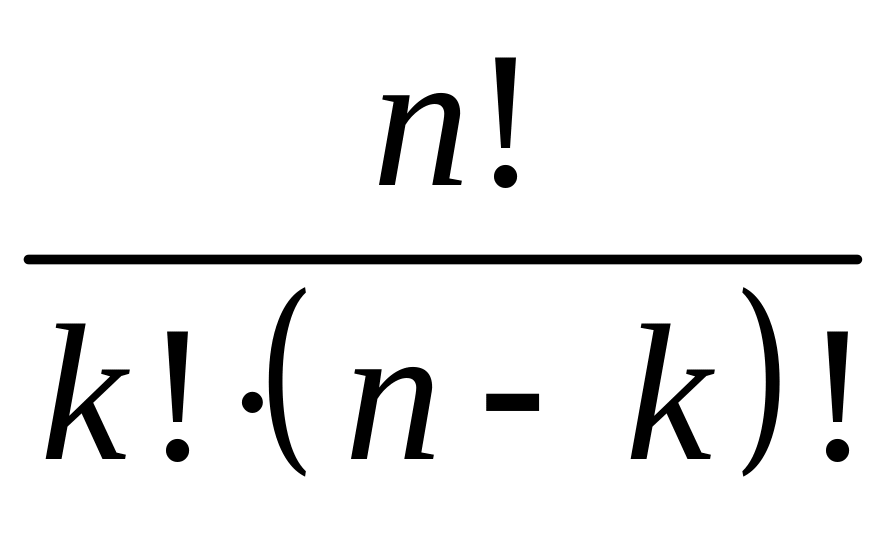 .
.
Кількість комбінацій з елементів по визначається за формулою:
а)
;
б)
 ;
в)
.
;
в)
.
Ймовірність появи події
 — це число, що знаходиться в межах:
— це число, що знаходиться в межах:
а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Сумою
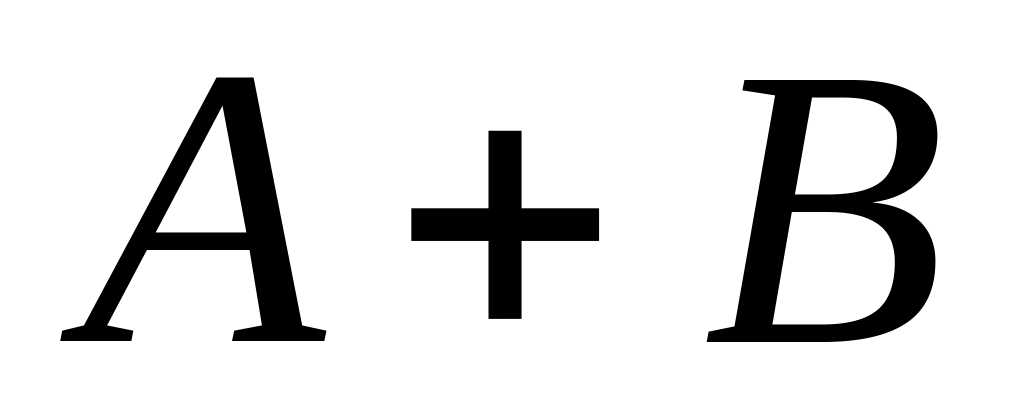 двох подій
і
двох подій
і
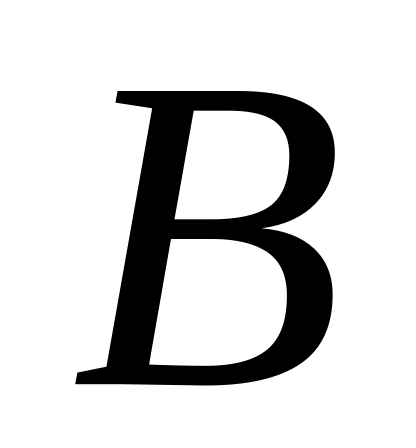 називається:
називається:
а) подія, що складається з усіх елементарних подій, які належать до подій і одночасно;
б) подія, що складається з усіх елементарних подій, які належать до події або ;
в) подія, що складається з усіх елементарних подій, які належать до події і не належать до події .
Добутком
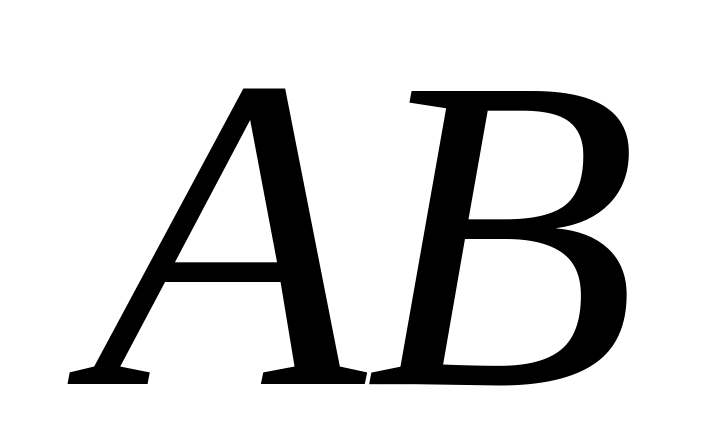 двох подій
і
називається:
двох подій
і
називається:
а) подія, що складається з усіх елементарних подій, які належать до події і не належать до події ;
б) подія, що складається з усіх елементарних подій, які належать до події або ;
в) подія, що складається з усіх елементарних подій, які належать до подій і одночасно.
Різницею
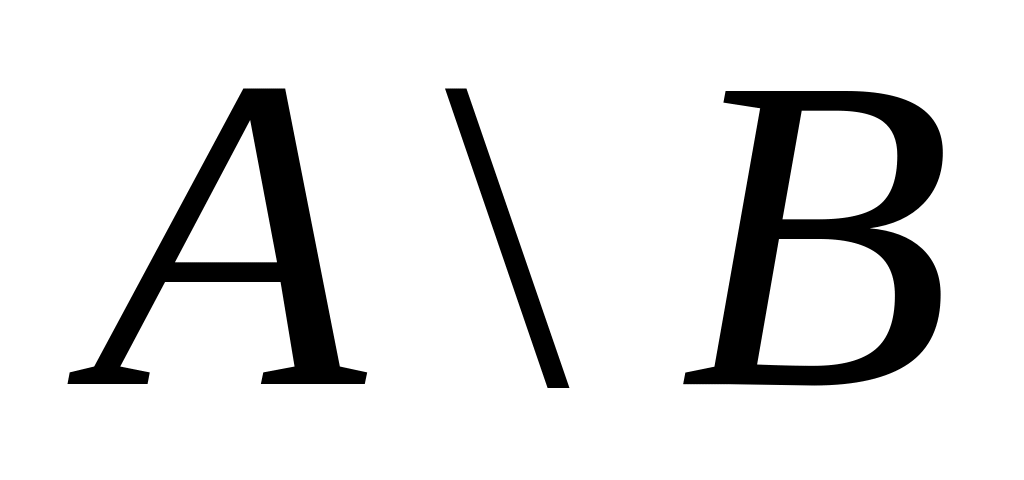 двох подій
і
називається:
двох подій
і
називається:
а) подія, що складається з усіх елементарних подій, які належать до подій і одночасно;
б) подія, що складається з усіх елементарних подій, які належать до події або ;
в) подія, що складається з усіх елементарних подій, які належать до події і не належать до події .
Протилежною подією
 до події
називається подія, для якої:
до події
називається подія, для якої:
а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дві події і називаються несумісними, якщо:
а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Ймовірність випадкової події у випадку рівноможливих елементарних події дорівнює відношенню:
а) кількості елементарних подій, з яких складається простір елементарних подій, до кількості елементарних подій, з яких складається подія ;
б) кількості елементарних подій, з яких складається подія , до кількості елементарних подій, з яких складається простір елементарних подій;
в) вірної відповіді нема.
Класичне означення ймовірності можна використовувати за умови, що елементарні події:
а) рівноможливі; б) довільні; в) нерівноможливі.
Ймовірність достовірної події дорівнює:
а)
1; б) 0;
в)
![]() .
.
Ймовірність неможливої події дорівнює:
а) ; б) 0; в) 1.
Ймовірність суми несумісних подій і дорівнює:
а)![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Ймовірність суми сумісних подій і дорівнює:
а) ;
б) ;
в) .
Якщо
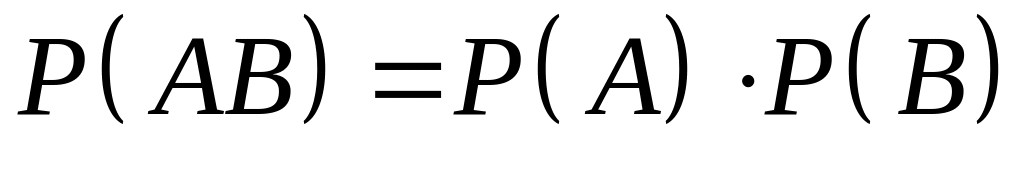 ,
то події
і
:
,
то події
і
:
а) несумісні; б) незалежні; в) залежні.
Ймовірність протилежної події визначають за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
В геометричному означенні ймовірності
 — це:
— це:
а)
кількості елементів
і
![]() відповідно;
відповідно;
б) найменші елементи множин і відповідно;
в) довжини, площі, об’єми множин і відповідно.
Умовною ймовірністю події за умови, що настала подія , називається число
 ,
для якого:
,
для якого:
а) ;
б)
;
б)
 ;
;
в)
 .
.
У формулі повної ймовірності
 :
:
а)![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Вказати формулу повної ймовірності:
а)![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Які з формул є формулами Байєса:
а)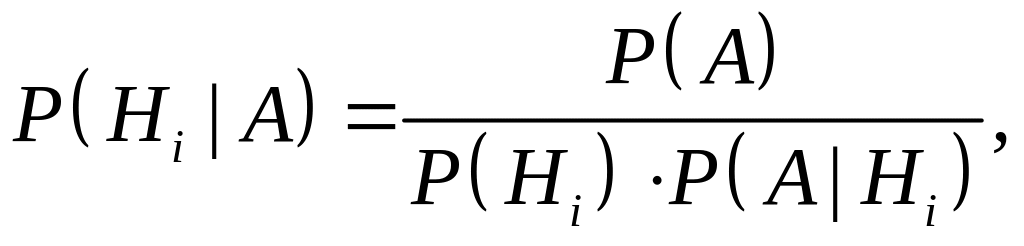
![]() ;
;
б)
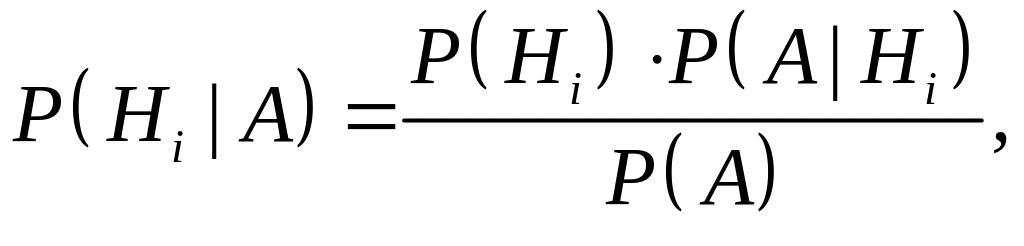 ;
;
в)
 .
.
Ймовірність
 того, що при
незалежних випробуваннях подія
настане
того, що при
незалежних випробуваннях подія
настане
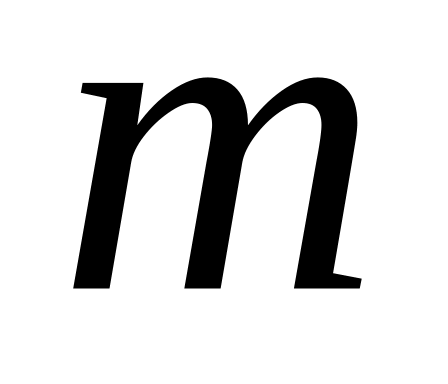 разів, визначають за формулою:
разів, визначають за формулою:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Ймовірність „невдачі” в одному випробуванні у схемі Бернуллі дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Ймовірність того, що при незалежних випробуваннях подія настане не менше, ніж разів, визначають за формулою:
а)
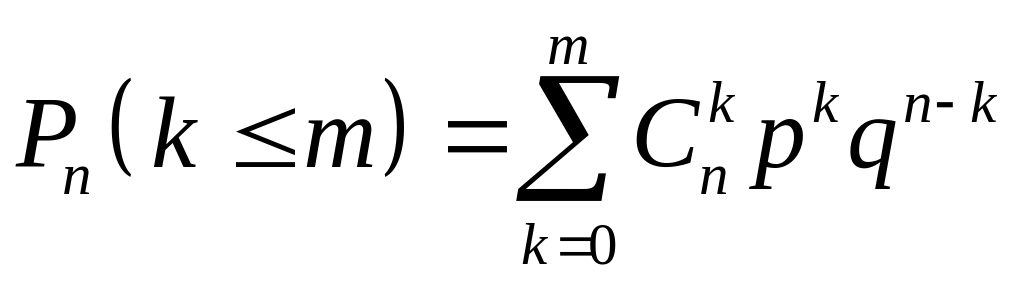 ;
б)
;
б)
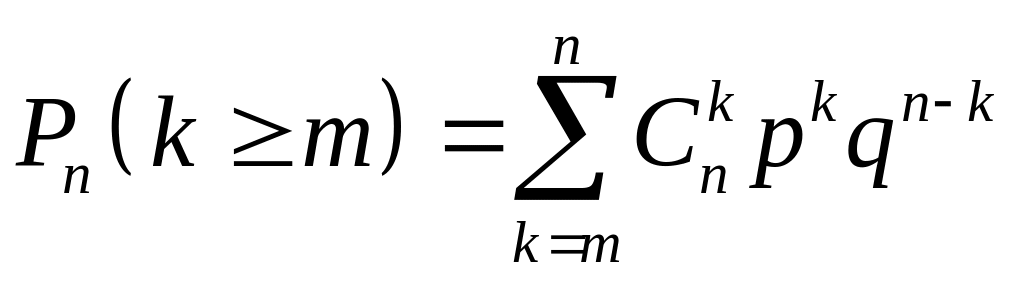 ;
;
в)
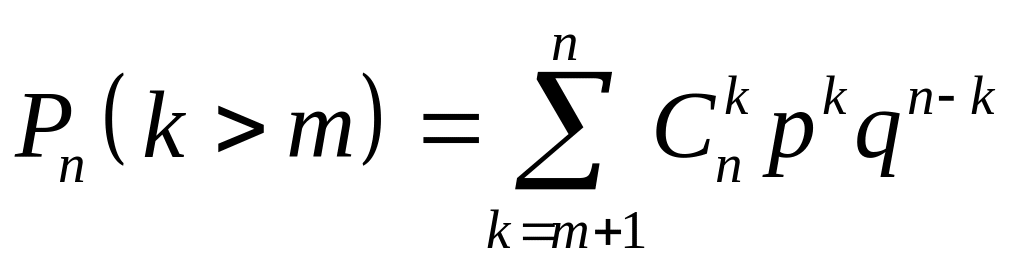 .
.
Ймовірність того, що при незалежних випробуваннях подія настане не більше, ніж разів, визначають за формулою:
а) ; б) ;
в)
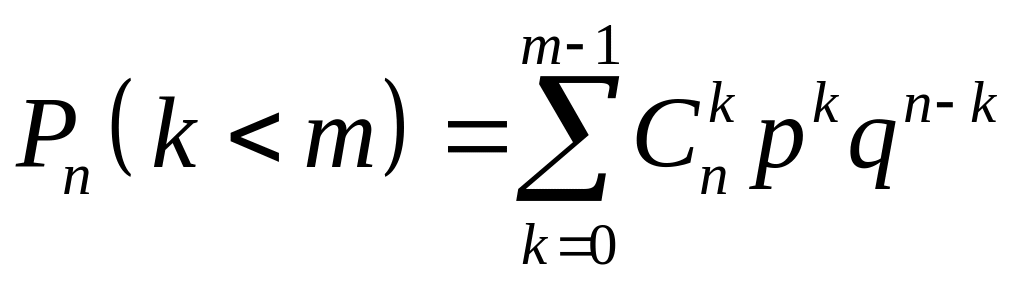 .
.
Якщо ймовірність
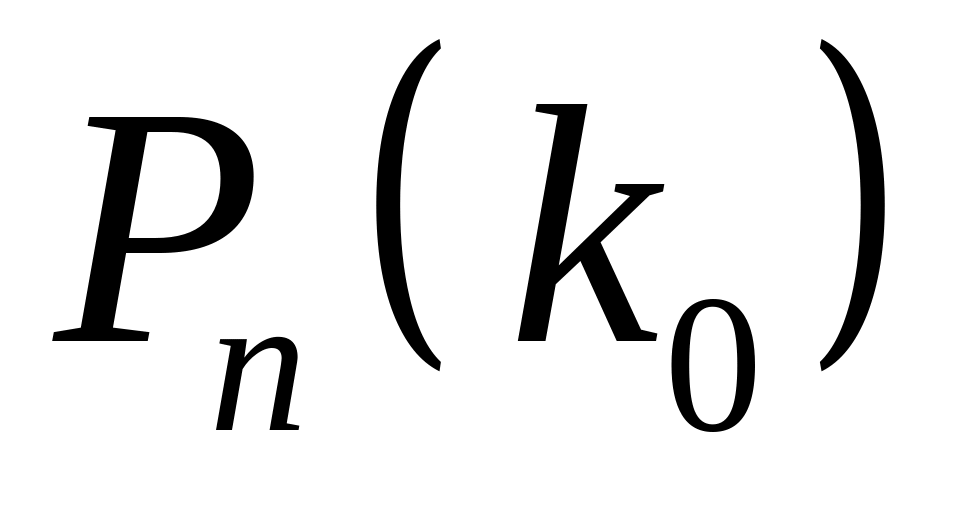 — найбільша із ймовірностей
— найбільша із ймовірностей
 ,
,
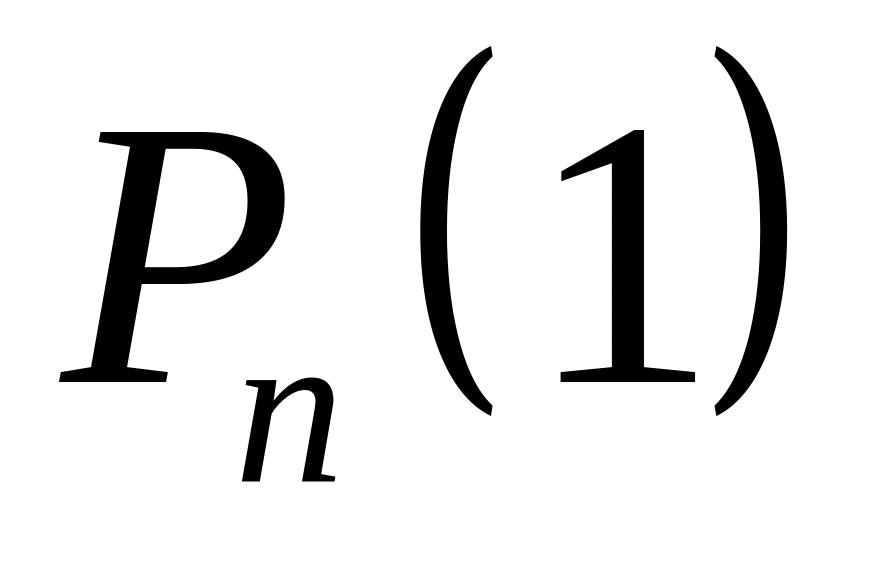 ,
,
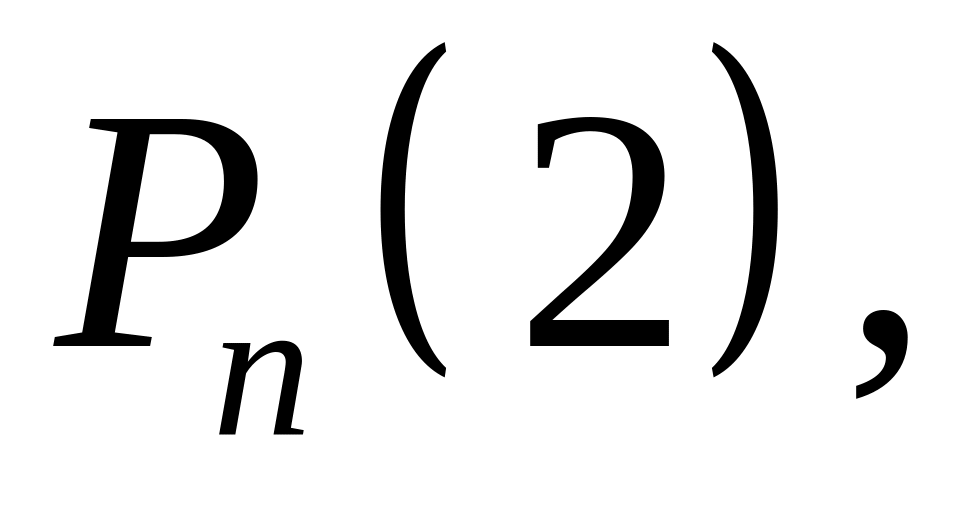

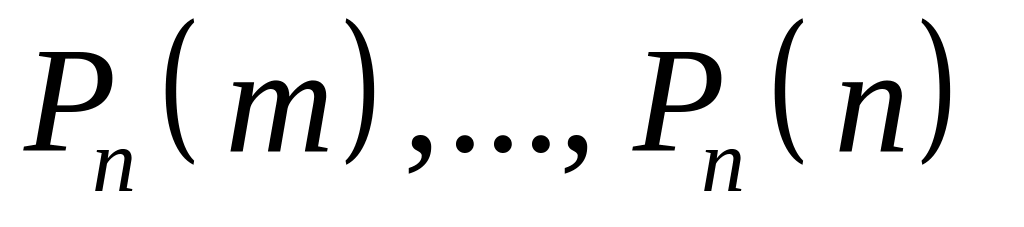 ,
то
,
то
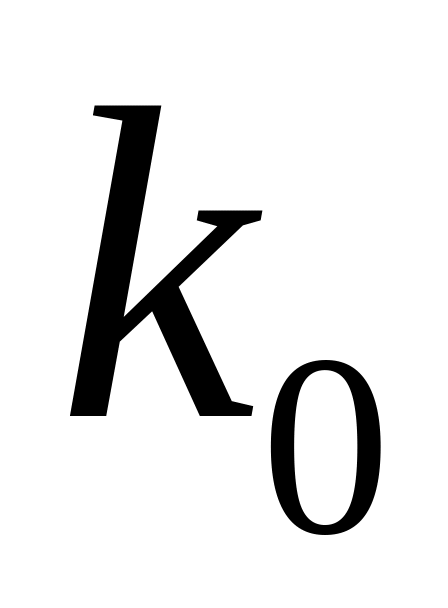 називають:
називають:
а) найімовірнішим числом „невдач”;
б) малоймовірним числом „успіхів”;
в) найімовірнішим числом „успіхів”.
Найімовірніше число „успіхів” у cхемі Бернуллі визначають із нерівності:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Найімовірніше число „успіхів” у cхемі Бернуллі:
а)
ціле число з проміжку
![]() ;
;
б) довільне число з проміжку ;
в) довільне ціле число.
При малих
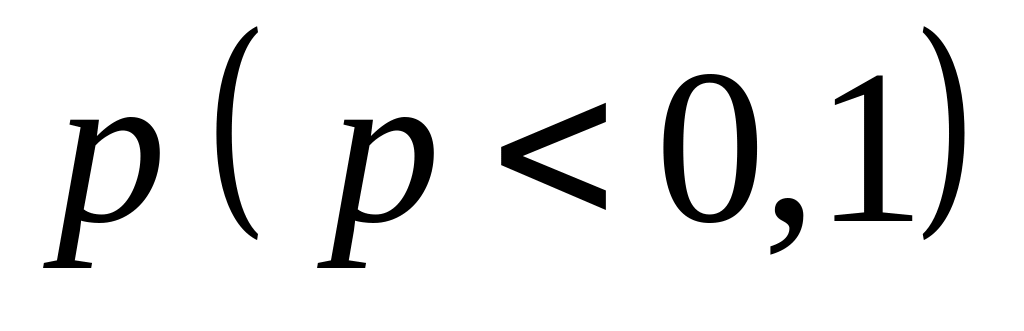 і великих
(однак
і великих
(однак
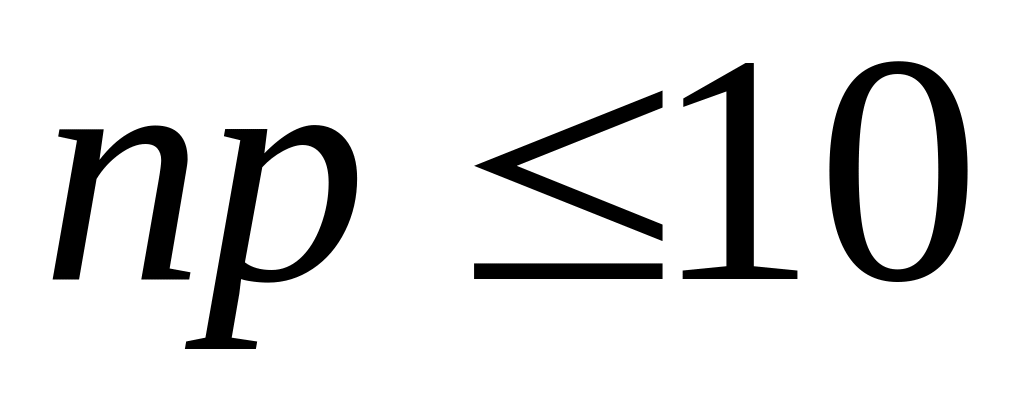 )
для знаходження ймовірності
)
для знаходження ймовірності
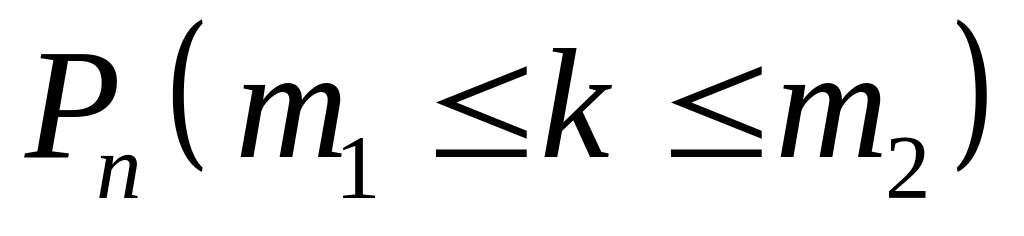 у схемі Бернуллі використовують формулу:
у схемі Бернуллі використовують формулу:
а) інтегральну Муавра-Лапласа;
б) локальну Муавра-Лапласа;
в) Пуассона.
В локальній теоремі Муавра-Лапласа
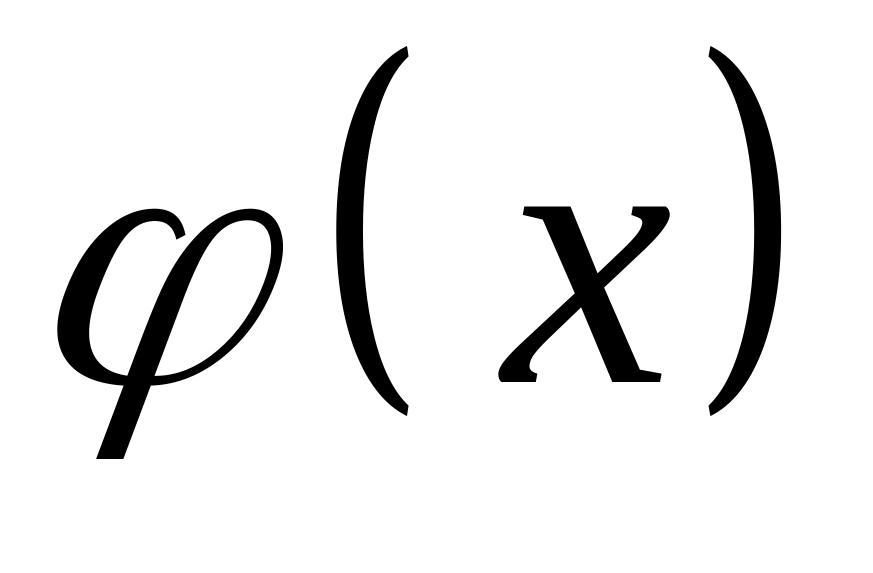 дорівнює:
дорівнює:
а)
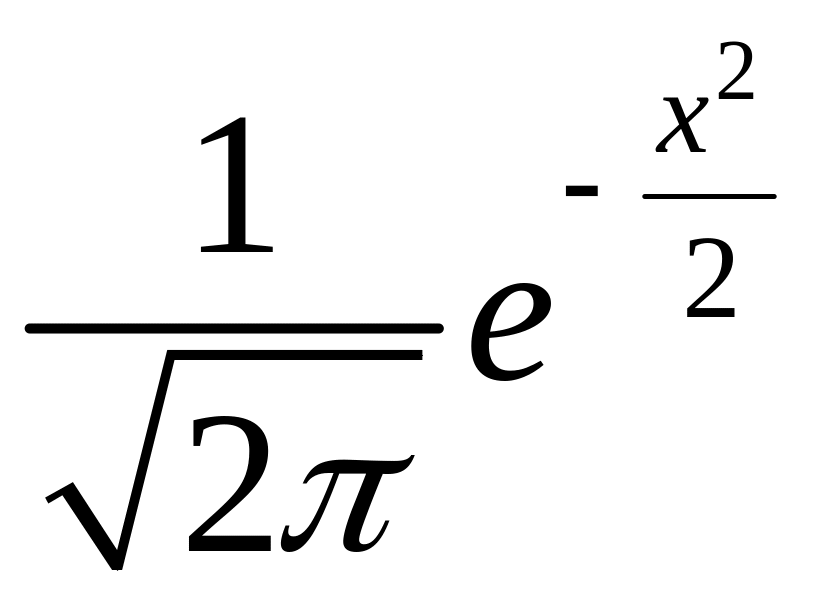 ;
б)
;
б)
 ;
в)
;
в)
 .
.
В інтегральній теоремі Муавра-Лапласа
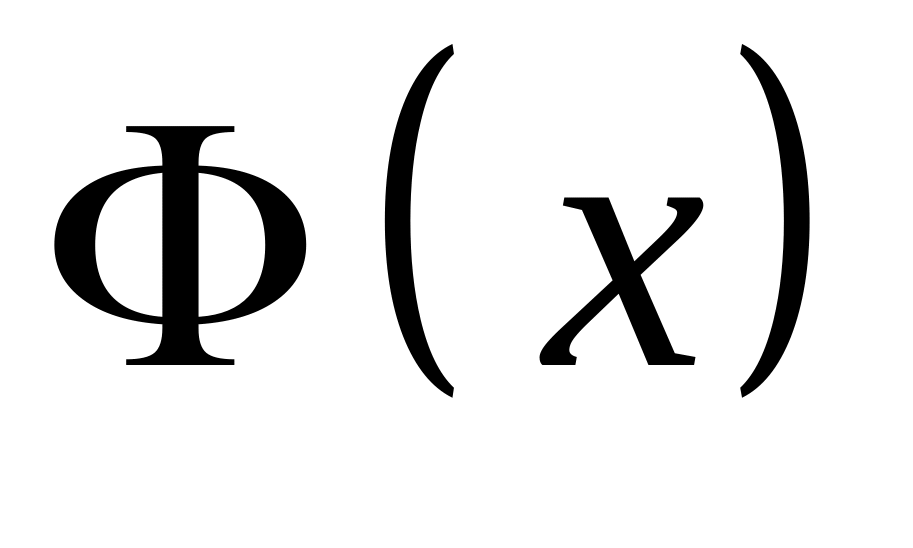 дорівнює:
дорівнює:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
В локальній формулі Муавра-Лапласа:
а)
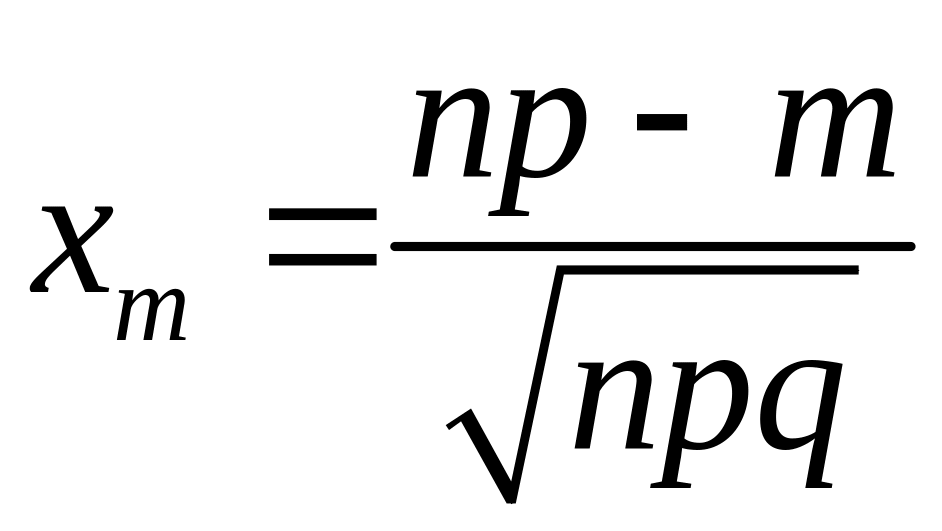 ;
б)
;
б)
 ;
в)
;
в)
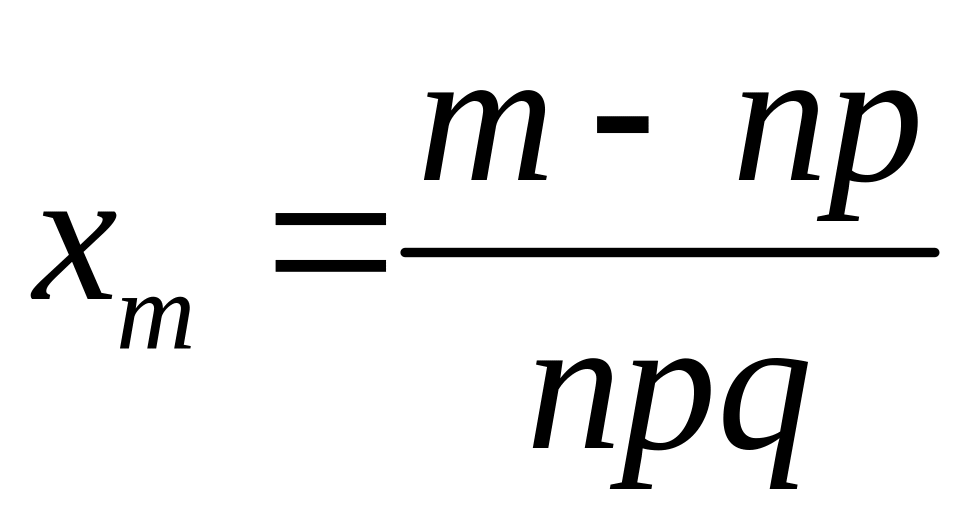 .
.
В інтегральній формулі Муавра-Лапласа:
а) ; б) ; в) .
Функція
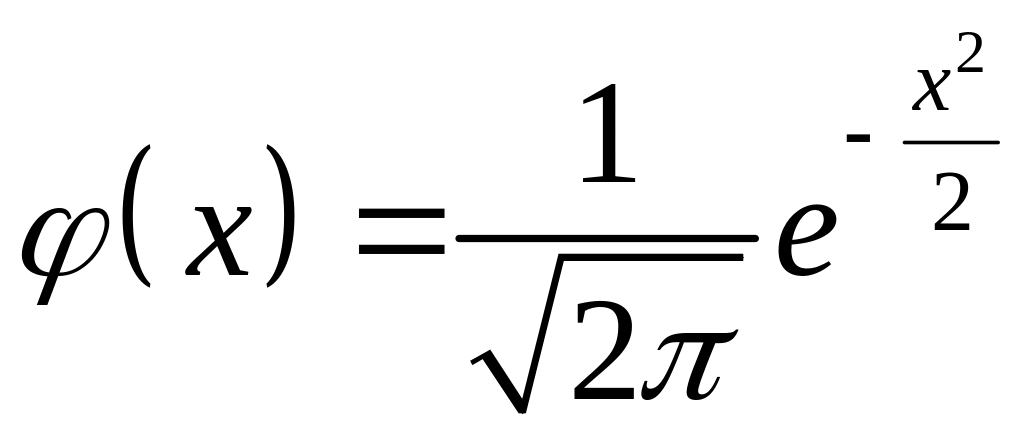 :
:
а) непарна; б) парна; в) ні парна, ні непарна.
Функція
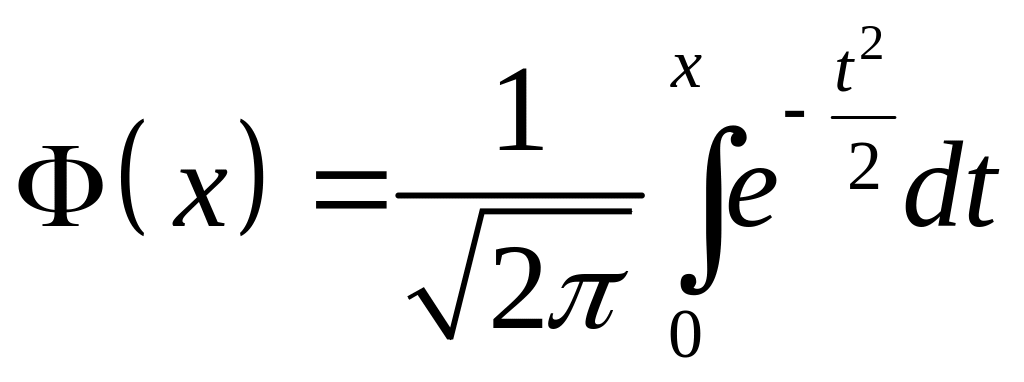 :
:
а) парна; б) ні парна, ні непарна; в) непарна.
Графік функції
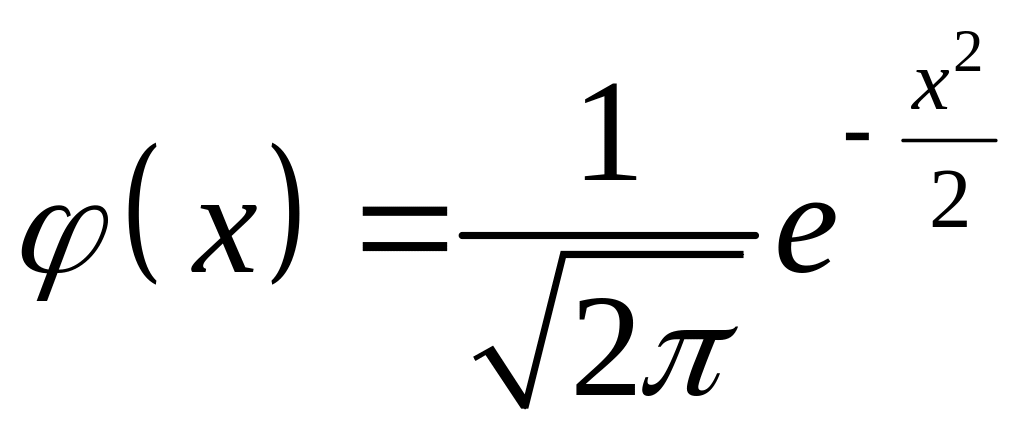 :
:
а) монотонно зростає на всій числовій осі;
б)
на інтервалі
![]() зростає і на інтервалі
зростає і на інтервалі
![]() спадає;
спадає;
в) на інтервалі спадає і на інтервалі зростає.
Графік функції :
а) монотонно зростає на всій числовій осі;
б) на інтервалі зростає і на інтервалі спадає;
в) на інтервалі спадає і на інтервалі зростає.
Якщо у схемі Бернуллі
 ,
то
,
то
а) ;
б)
;
б)
 ;
в)
;
в)
 .
.
В теоремі Бернуллі:
а)
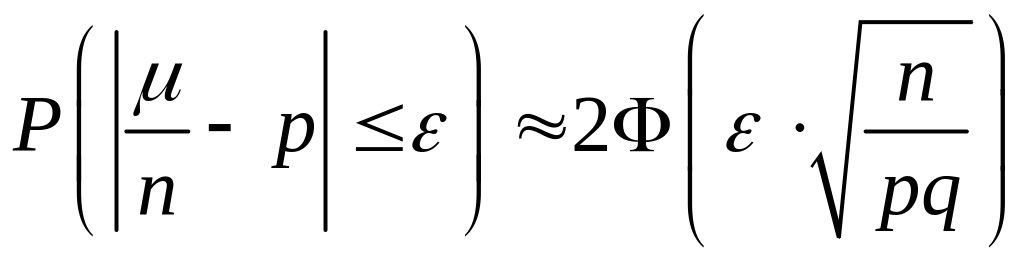 ;
б)
;
б)
 ;
;
в)
 .
.
Випадкова величина — це:
а) випадкове число, яке отримуємо в незалежному експерименті;
б) числова функція, яка задана на просторі елементарних подій;
в) число, яке дорівнює ймовірності настання події.
Функція розподілу випадкової величини
 — це:
— це:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Для функції розподілу
 :
:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Функція розподілу випадкової величини є:
а) незростаюча на всій числовій осі;
б) неспадна на всій числовій осі;
в) спадна на всій числовій осі.
Функція розподілу випадкової величини:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Для функції розподілу:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Функція розподілу випадкової величини:
а) неперервна; б) неперервна зліва; в) неперервна справа.
Випадкова величина називається випадковою величиною дискретного типу, якщо:
а) вона набуває скінченних або зчисленних значень;
б) значення, яких вона набуває, є дискретними;
в) множина її можливих значень скінченна або зчисленна.
Випадкова величина називається випадковою величиною неперервного типу, якщо:
а) множина її можливих значень скінченна або зчисленна;
б) значення, яких вона набуває, є неперервними;
в) множина
її можливих значень представляє собою
деякий інтервал
![]() (скінченний або нескінченний) числової
прямої.
(скінченний або нескінченний) числової
прямої.
Випадкову величину називають неперервною , якщо її функцію розподілу можна подати у вигляді:
а)
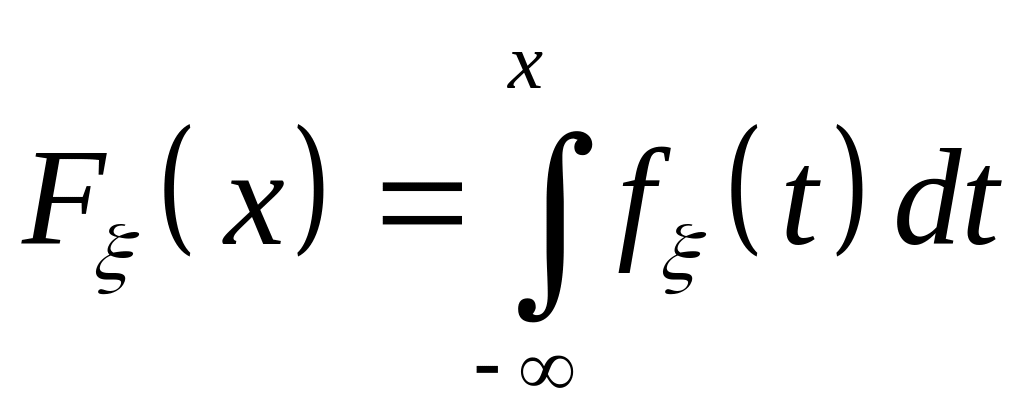 ;
б)
;
б)
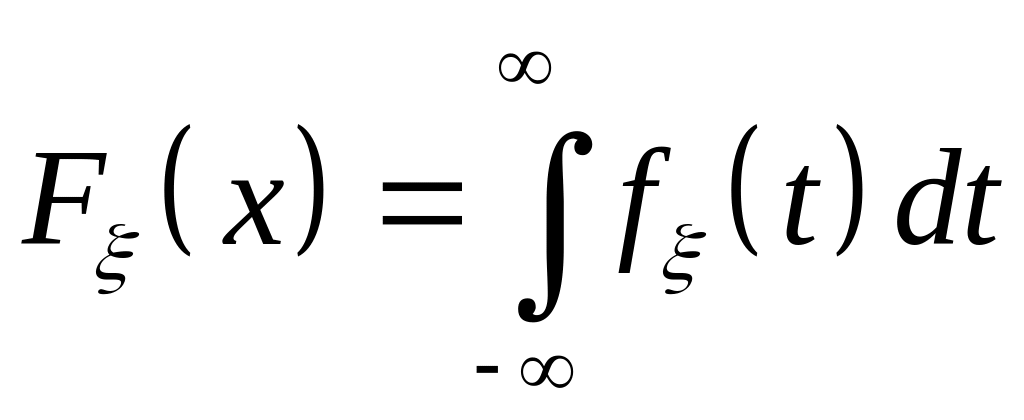 ;
в)
;
в)
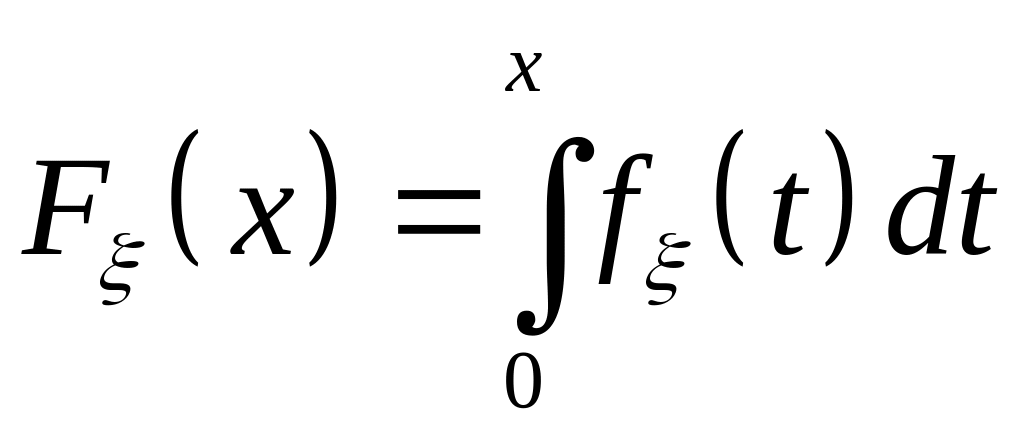 .
.
Для густини розподілу:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
Густина розподілу:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
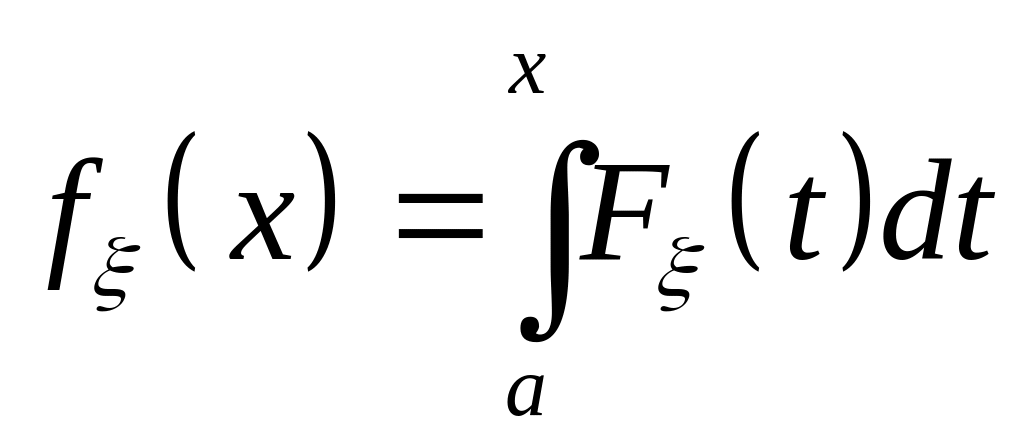 .
.
Для неперервної випадкової величини:
а)
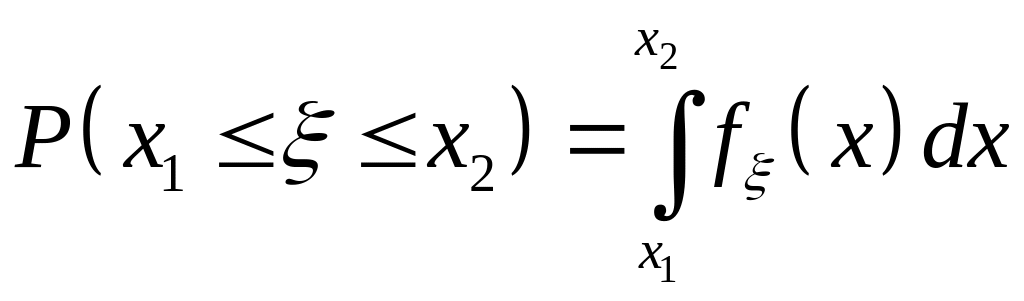 ;
б)
;
б)
 ;
;
в)
 .
.
Математичне сподівання дискретної випадкової величини :
а)
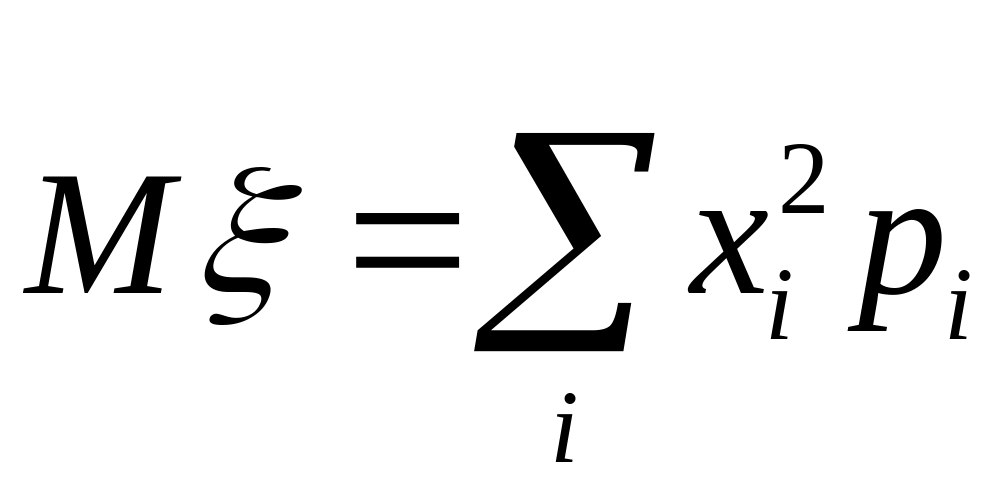 ;
б)
;
б)
 ;
в)
;
в)
 .
.
Математичне сподівання неперервної випадкової величини :
а)
 ;
б)
;
б)
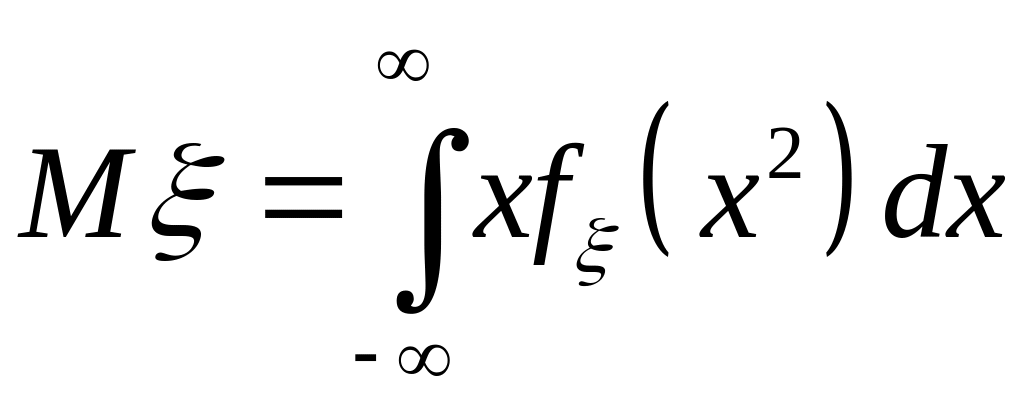 ;
в)
;
в)
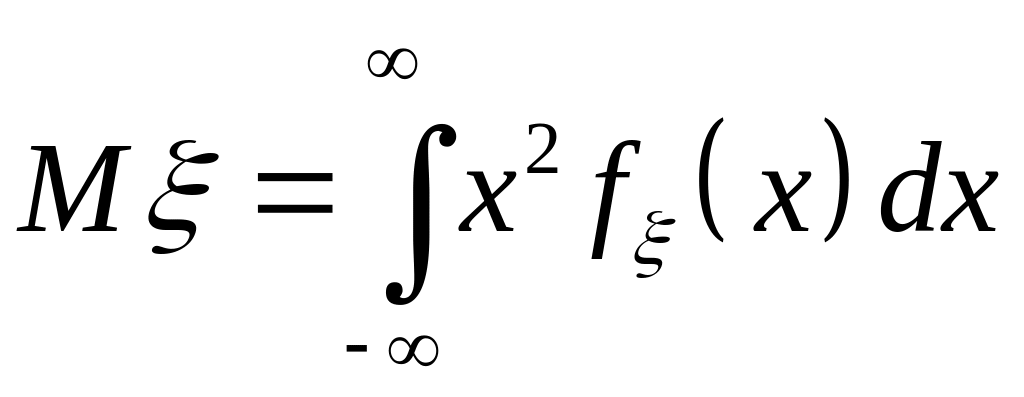 .
.
Дисперсія випадкової величини :
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дисперсія випадкової величини :
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дисперсія неперервної випадкової величини :
а)
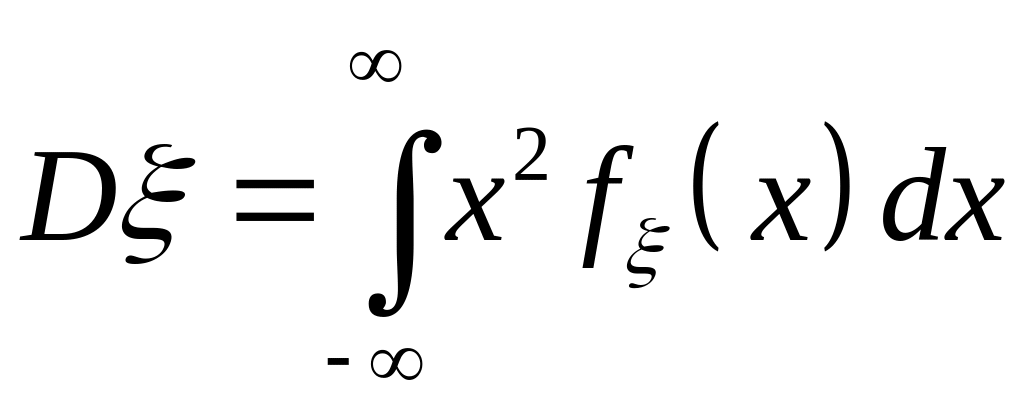 ;
б)
;
б)
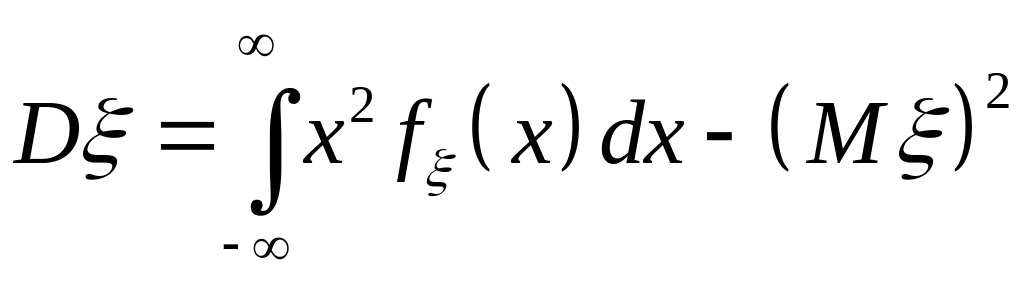 ;
;
в).
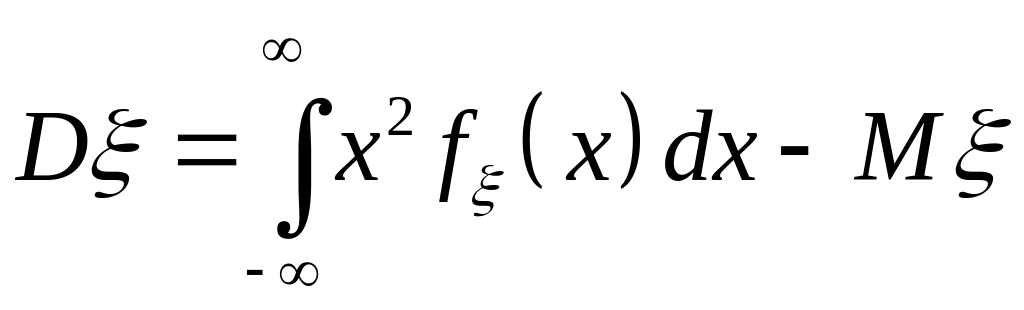
Дисперсія неперервної випадкової величини :
а)
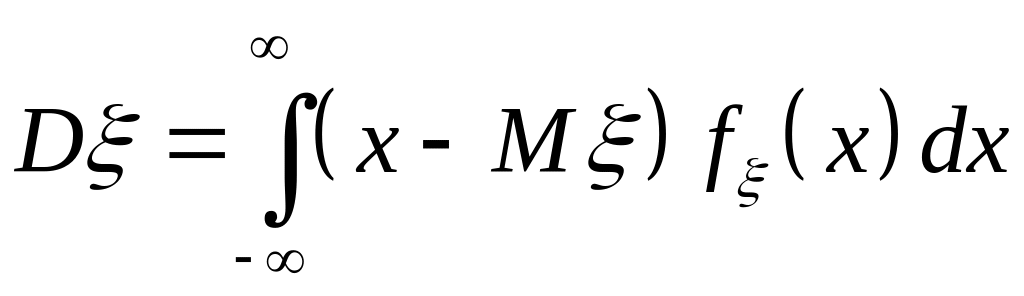 ;
б)
;
б)
 ;
;
в)
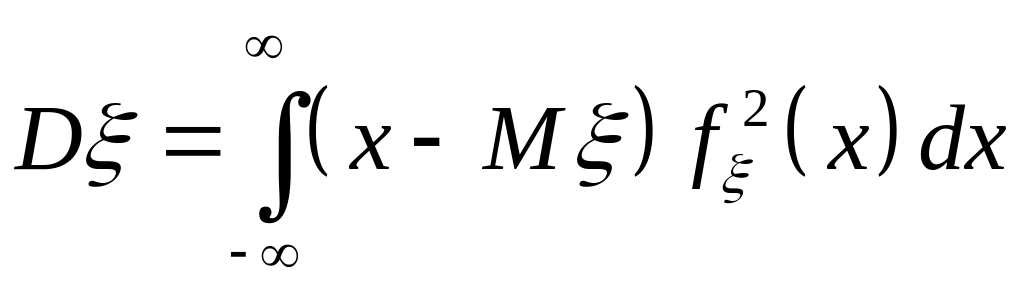 .
.
Дисперсія дискретної випадкової величини :
а)
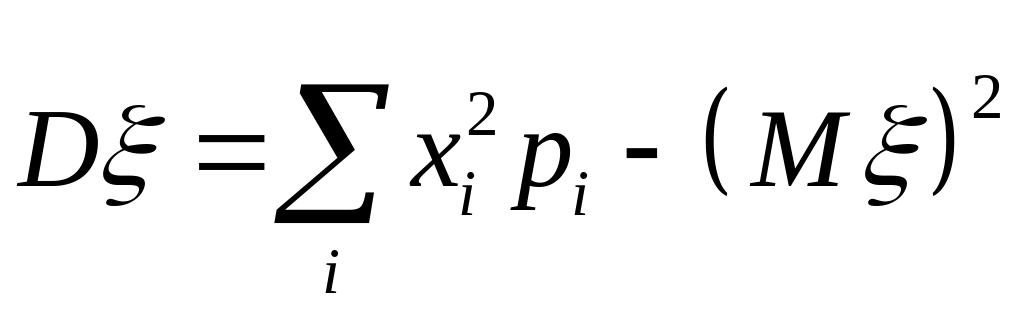 ;
б)
;
б)
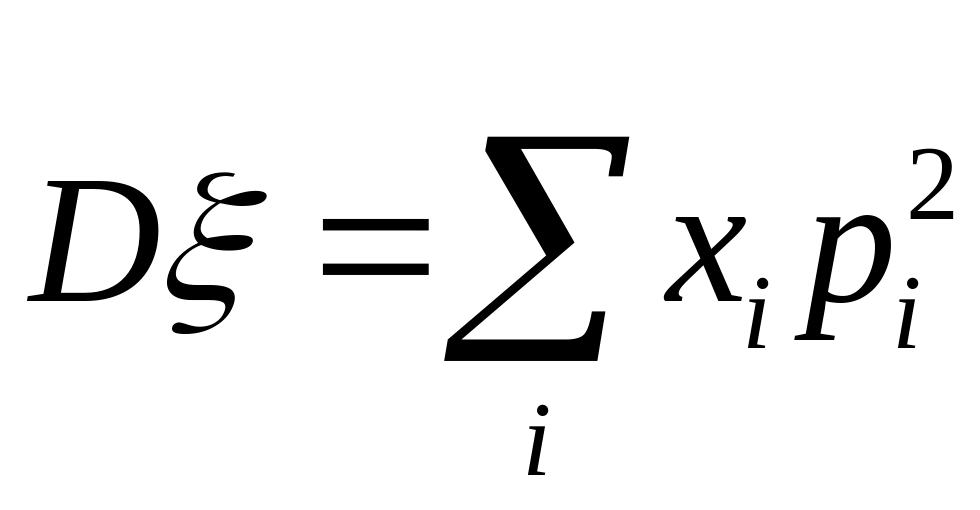 ;
в)
;
в)
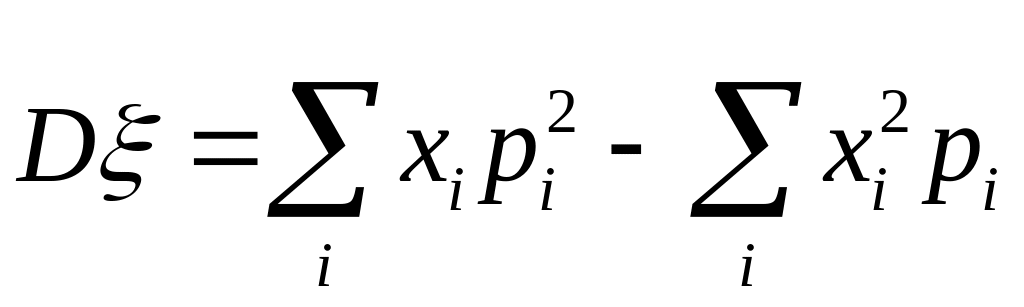
Середнє квадратичне відхилення випадкової величини :
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дисперсія дискретної випадкової величини :
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() .
.
Моментом -го порядку випадкової величини відносно точки називається число:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Центральним моментом -го порядку випадкової величини називається момент -го порядку випадкової величини відносно точки , яка дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Початковим моментом -го порядку випадкової величини називається момент -го порядку випадкової величини відносно точки , яка дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
.
;
в)
.
Коефіцієнт асиметрії обчислюється за формулою:
а)
 ;
б)
;
б)
 ;
в)
;
в)
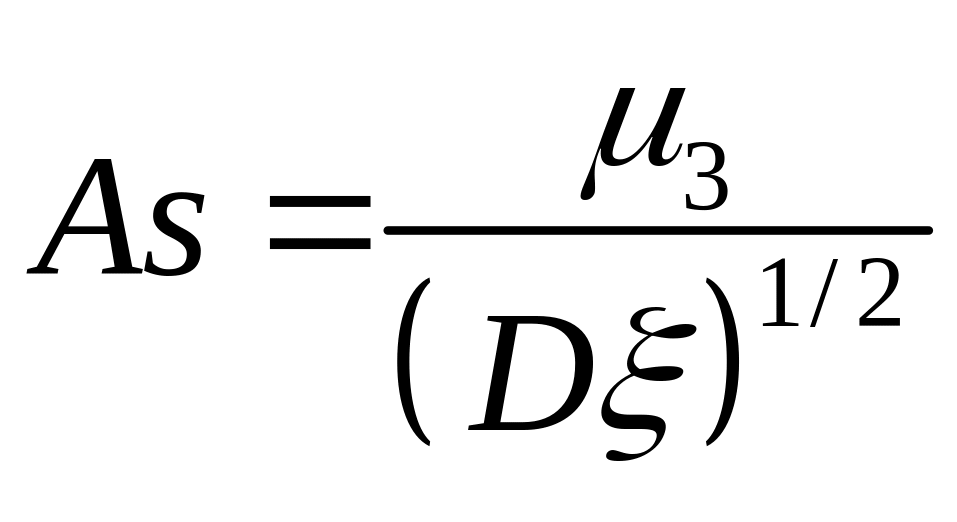 .
.
Коефіцієнт ексцесу обчислюється за формулою:
а)
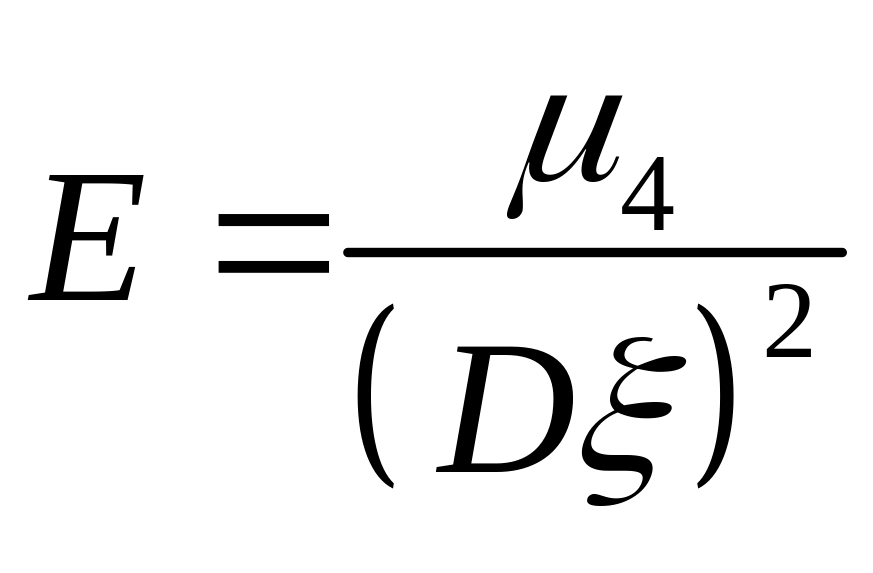 ;
б)
;
б)
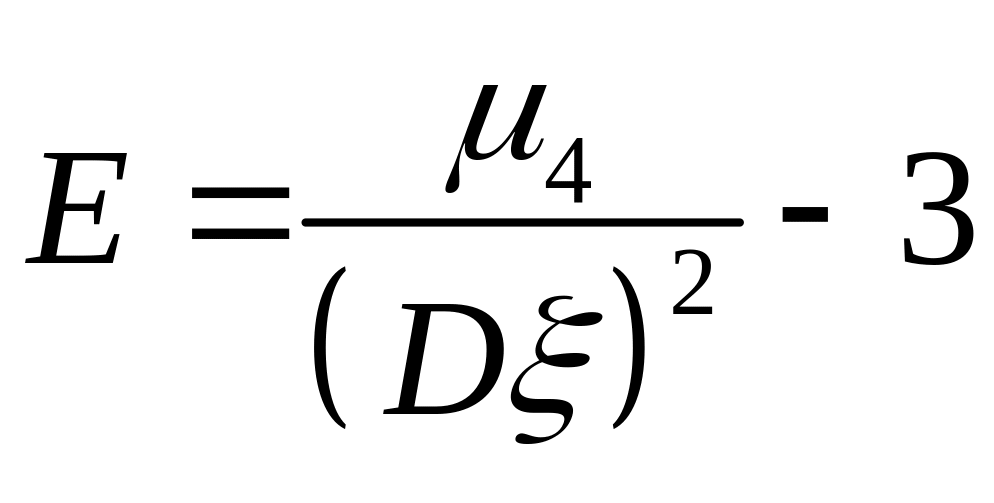 ;
в)
;
в)
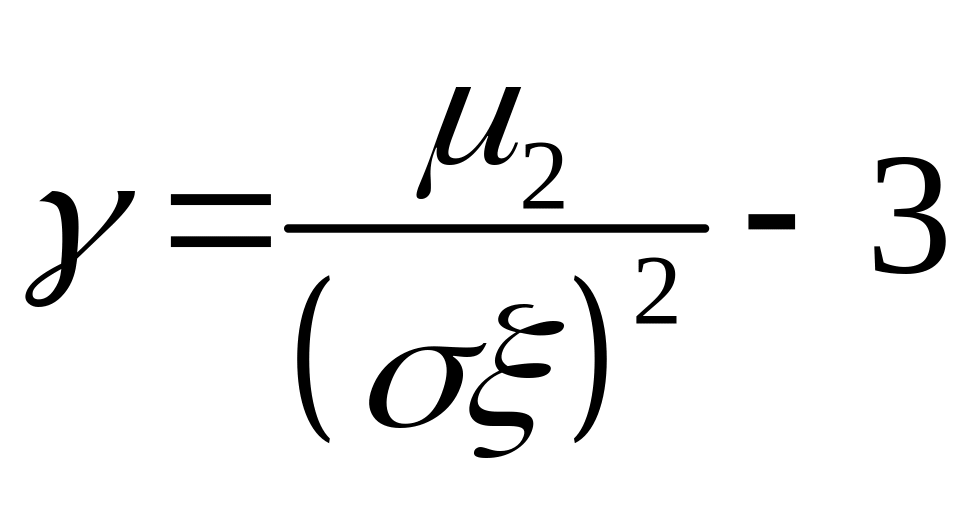 .
.
Нормальним називається розподіл, густина якого дорівнює:
а)
 ;
б)
;
б)
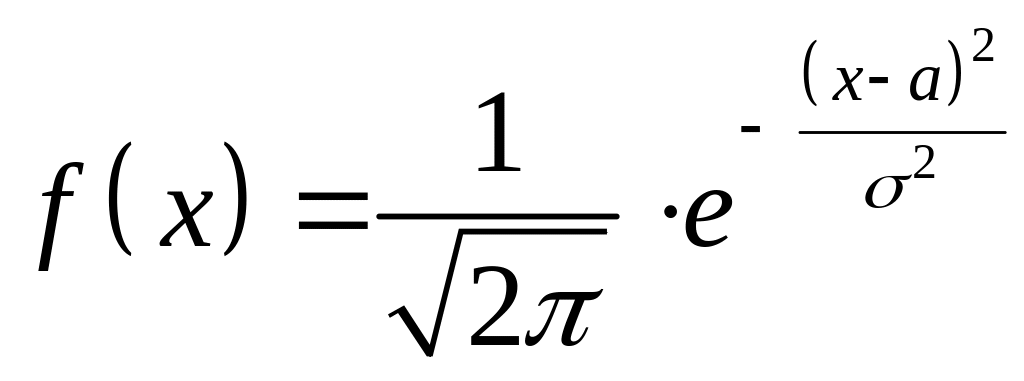 ;
в)
;
в)
 .
.
Для нормального закону розподілу:
а)
![]() ,
,
![]() ;
б)
,
;
б)
,
![]() ;
в)
;
в)
![]() ,
.
,
.
Нормальний розподіл називається стандартним нормальним розподілом, якщо густина дорівнює:
а)
 ;
б)
;
б)
 ;
в)
;
в)
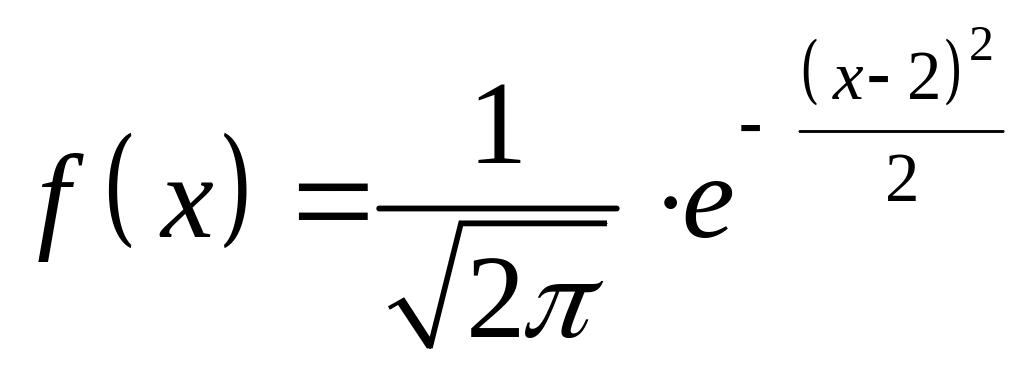 .
.
Випадкова величина називається рівномірно розподіленою на інтервалі
 ,
якщо густина:
,
якщо густина:
а)
 ;
б)
;
б)
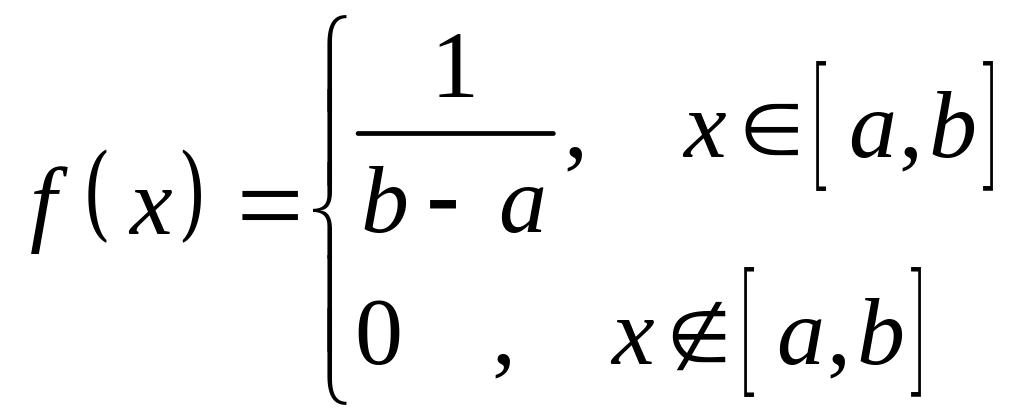 ;
;
в)
 .
.
Математичне сподівання випадкової величини , що розподілена за біномним законом, дорівнює:
а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() .
.
Дисперсія випадкової величини , що розподілена за біномним законом, дорівнює:
а)
![]() ; б)
;
в)
.
; б)
;
в)
.
Математичне сподівання випадкової величини , що розподілена за законом Пуассона, дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дисперсія випадкової величини , що розподілена за законом Пуассона, дорівнює:
а)
;
б)
;
в)
![]() .
.
Математичне сподівання нормально розподіленої випадкової величини дорівнює:
а)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дисперсія нормально розподіленої випадкової величини дорівнює:
а)
![]() ;
б)
;
в)
;
б)
;
в)
![]() .
.
Математичне сподівання рівномірно розподіленої на інтервалі випадкової величини дорівнює:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Дисперсія рівномірно розподіленої на інтервалі випадкової величини дорівнює:
а)
![]() ;
б)
;
б)
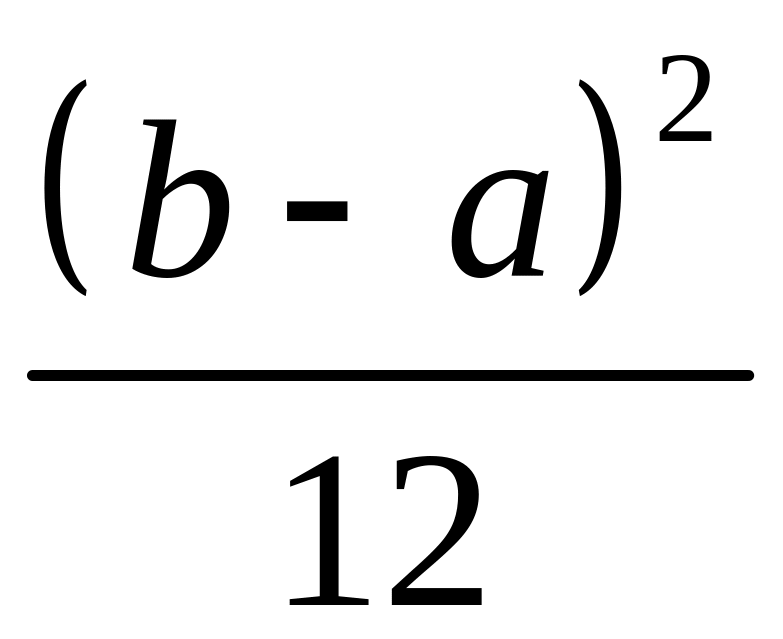 ;
в)
;
в)
![]() .
.
Яке з тверджень правильне:
а) об’єм генеральної сукупності перевищує об’єм вибіркової сукупності;
б) обсяг вибіркової сукупності перевищує обсяг статистичної сукупності;
в) об’єм вибірки дорівнює об’єму генеральної сукупності.
Кількість повторів елемента у вибірці називають:
а) рангом; б) відносною частотою; в) частотою.
Графічне зображення статистичного ряду у вигляді ламаної лінії називають:
а) гістограмою; б) полігоном; в) графіком вибірки.
Точкова оцінка
 параметра
параметра
 розподілу генеральної сукупності
називається незміщеною, якщо:
розподілу генеральної сукупності
називається незміщеною, якщо:
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() .
.
Точкова оцінка параметра розподілу генеральної сукупності називається ефективною, якщо вона:
а) змістовна і незміщена;
б) має найбільшу дисперсію серед усіх можливих незміщених оцінок параметра ;
в) має найменшу дисперсію серед усіх можливих незміщених оцінок параметра .
Незміщеною і змістовною точковою оцінкою математичного сподівання в генеральній сукупності є:
а) вибіркова дисперсія;
б) вибіркове середнє;
в) немає правильної відповіді.
Незміщеною і змістовною точковою оцінкою дисперсії в генеральній сукуп- ності є:
а) вибіркова дисперсія;
б) вибіркове середнє;
в) виправлена вибіркова дисперсія.
Зміщеною і змістовною точковою оцінкою дисперсії в генеральній сукупності є:
а) вибіркова дисперсія;
б) вибіркове середнє;
в) виправлена вибіркова дисперсія.
Вибіркове середнє
 :
:
а) завжди додатне;
б) завжди невід’ємне;
в) може бути як додатним, так і від’ємним.
Вибіркова дисперсія
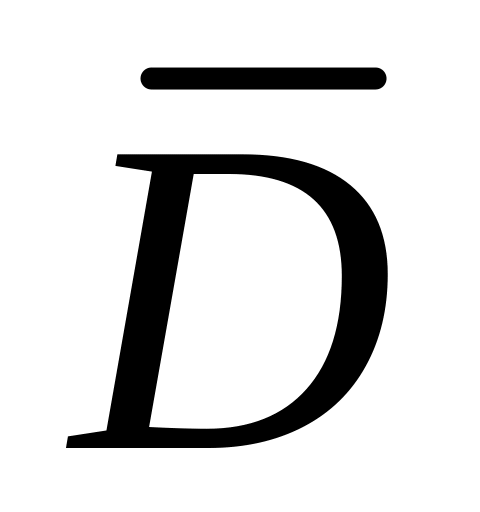 :
:
а) завжди додатна;
б) завжди невід’ємна;
в) може бути як додатною, так і від’ємною.
Якщо
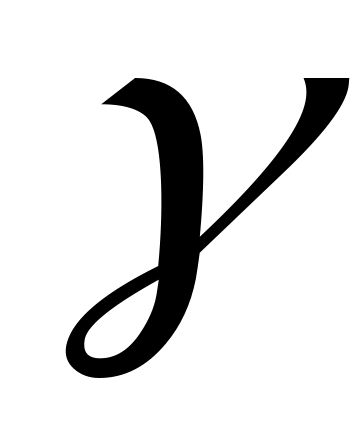 — довірчий рівень, то величина
— довірчий рівень, то величина
 називається:
називається:
а) рівнем надійності;
б) рівнем значущості;
в) довірчою ймовірністю.
При збільшенні рівня надійності довірчий інтервал:
а) розширюється; б) звужується; в) залишається без змін.
Якщо спостережуване значення статистики потрапляє в критичну область, то:
а) немає підстав відхиляти нульову гіпотезу;
б) нульову гіпотезу відхиляють на користь альтернативної;
в) область прийняття гіпотези порожня.
Статистичну гіпотезу про рівність дисперсій двох незалежних нормально розподілених ознак генеральної сукупності перевіряють за допомогою:
а) критерію Стьюдента; б) рівняння Лапласа; в) критерію Фішера.
У критерії (Пірсона) для перевірки гіпотези про вид розподілу використовують статистику:
а)
 ;
б)
;
б)
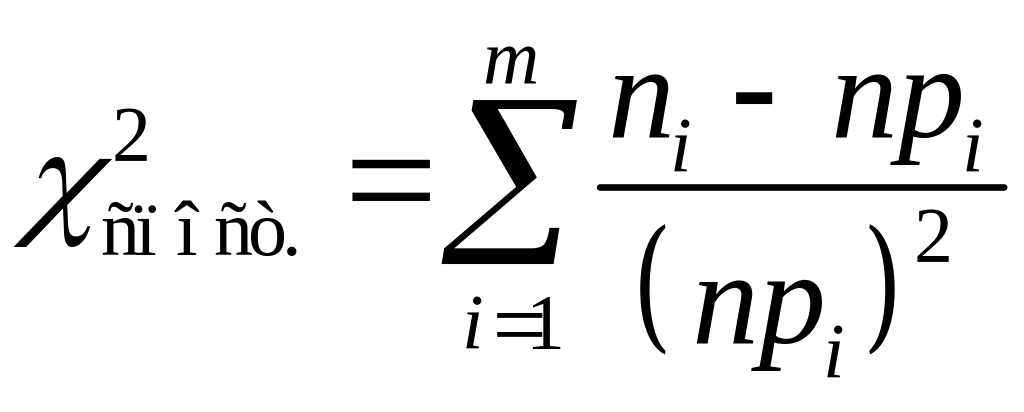 ;
в)
;
в)
 .
.
Для вибіркового коефіцієнта кореляції
 справедлива нерівність:
справедлива нерівність:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Для коефіцієнта детермінації
 справедлива нерівність:
справедлива нерівність:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Для парної лінійної регресії між коефіцієнтом детермінації та вибірковим коефіцієнтом кореляції справедливе таке співвідношення:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Вибіркове лінійне рівняння регресії визначають у вигляді:
а)
![]() б)
б)
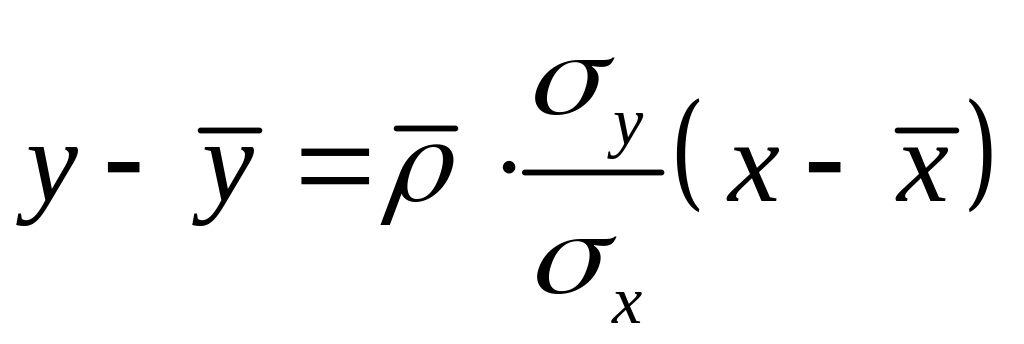 ;
в) усі відповіді правильні.
;
в) усі відповіді правильні.
Значущість коефіцієнта кореляції при великому об’ємі вибірки перевіряють за допомогою:
а) рівняння Лапласа;
б) критерію Стьюдента;
в) критерію Фішера.
