Семестровая работа №2. Предел функции. Дифференциальное исчисление функции одной переменной.
1. Вычислить пределы.
Вариант 1
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 2
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 3
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 4
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 5
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 6
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 7
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 8
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 9
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 10
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 11
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 12
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 13
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 14
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 15
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 16
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 17
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 18
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 19
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 20
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
9)
;
10)
.
Вариант 21
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 22
1)
;
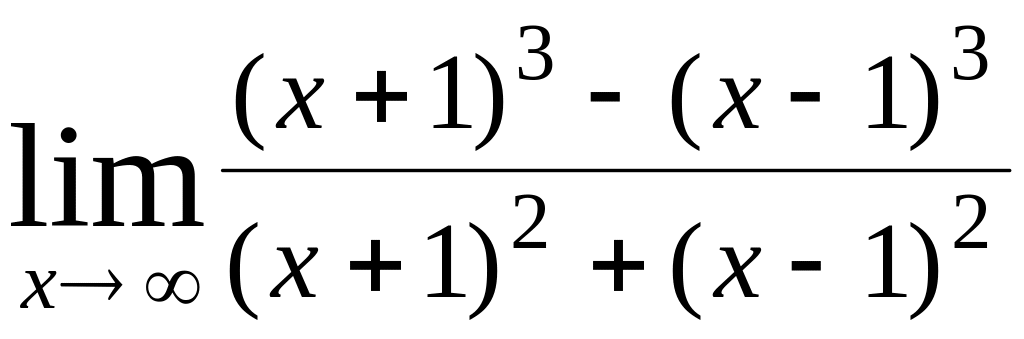2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 23
1)
;
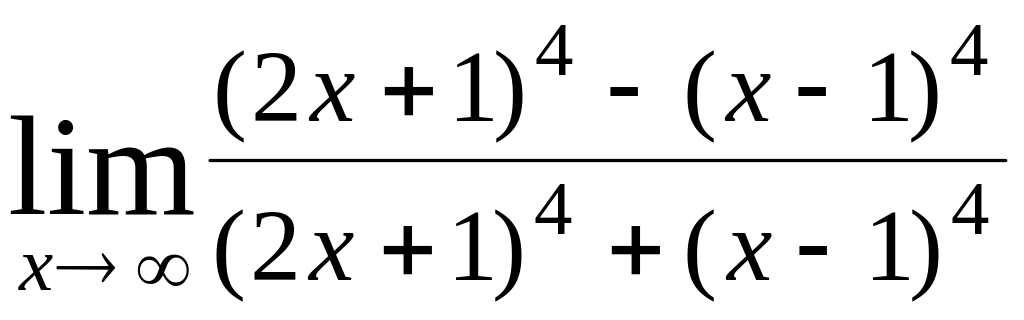2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 24
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 25
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 26
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 27
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 28
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 29
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
Вариант 30
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
2. Показать, что функции f(x) и (x) являются бесконечно малыми или бесконечно большими одного порядка.
|
при
|
11.
при
|
21.
при
|
|
при |
12.
при |
22.
при |
|
при |
13. при |
23.
при |
|
при |
14.
при
|
24.
при |
|
при
|
15. при |
25. при |
|
при
|
16.
при |
26. при |
|
при |
17. при |
27.
при |
|
при |
18.
при |
28.
при |
|
при |
19.
при |
29.
при |
|
при |
20.
при |
30.
при |
3. Задана функция y=f(x). Требуется найти точки разрыва, если они существуют. Сделать чертеж.
1.
|
11.
|
21.
|
2.
|
12. |
22.
|
3.
|
13.
|
23.
|
4.
|
14.
|
24.
|
5.
|
15.
|
25.
|
6. |
16.
|
26.
|
7.
|
17.
|
27.
|
8.
|
18.
|
28.
|
9.
|
19.
|
29.
|
10.
|
20.
|
30.
|
4. Задана функция y=f(x) и два значения аргумента x1 и x2. Требуется установить, является ли данная функция непрерывной или разрывной для каждого из значений x и найти ее односторонние пределы в этих точках.
1.
|
11.
|
21.
|
2.
;
|
12.
; . |
22.
|
3.
|
13.
|
23.
|
4.
|
14.
;
|
24.
|
5.
|
15.
|
25.
; |
6.
|
16.
; |
26.
|
7.
|
17.
;
|
27.
; . |
8.
; . |
18.
|
28.
;
|
9.
; |
19.
;
|
29.
;
|
10.
|
20.
; . |
30.
|
;
;
.
;
;
;
;
.
;
;
;
;
;
;
;
;
;
;
;
;
.
;
.
;
;
.
;
;
.
;
;
.
;
;
;
;
;
;
;
;
;
.
;
;
;
;
.
;
;
;
.
;
.
;
;
;
;
;
