Отчётные материалы

1. Расчет параметров структурной схемы динамической модели контура скорости.

2. Расчет параметров аналогового регулятора скорости.

3. Электрическая схема аналогового регулятора скорости.

4. Структурная схема динамической модели контура скорости.

5. Графики зависимостей угловой скорости от времени скорректированного контура скорости по сигналу задания и моменту сопротивления и их анализ.

6. ЛЧХ и их анализ.

Контрольные вопросы

1. Дать определение настройки на ОМ.

2. Дать определение настройки на СО.

3. Записать передаточную функцию замкнутого контура настроенного

на ОМ.

4. Записать передаточную функцию разомкнутого контура настроенного на СО.

5. Перечислить показатели качества переходного процесса с применением стандартных настроек.

6. Записать передаточную функцию ПИД-регулятора.

7. Начертить электрическую схему ПИД-регулятора.

8. Изложить порядок моделирования контура скорости с применением системы MatLab.

ЛАБОРАТОРНАЯ РАБОТА № 4

ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ЦИФРОВОГО РЕГУЛЯТОРА

СКОРОСТИ И МОДЕЛИРОВАНИЕ КОНТУРА СКОРОСТИ

1. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ

НЕПРЕРЫВНЫХ СТАЦИОНАРНЫХ СИСТЕМ

В современной теории управления широко применяется метод пространства состояний, который базируется на математических моделях в переменных состояния [5, 6, 8, 9, 11, 13, 15, 16]. Такая математическая модель представляет собой систему уравнений первого порядка, которую обычно представляют в векторно-матричной форме. Преимущество такого представления заключается в том, что облегчается решение задач анализа и синтеза с применением ЦВМ на этапе проектирования.

Динамические свойства линейной непрерывной стационарной системы описываются векторно-матричными уравнениями

, (4.1)

, (4.2)

где х^T=[x₁ x₂ . . . x_n] – вектор-состояния размерности (n1);

u^T=[u₁ u₂ . . . u_m] – вектор-входа размерности (m1);

y^T=[y₁ y₂ . . . y_q] – вектор-выхода размерности (q1);

A, B, C и D – матрицы коэффициентов размерности (nn), (nm), (qn), (qm), соответственно.

Уравнение (4.1) связывает переменные состояния и входные переменные и называется уравнением состояния. Уравнение (4.2) связывает выходные переменные с переменными состояния и входными переменными, и называется уравнением выхода.

На рис. 4.1 изображена векторная структурная схема линейной непрерывной стационарной системы, построенная по уравнениям (4.1) и (4.2).

u

y

x

D

С

А

В

s^-1

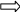
Рис. 4.1. Векторная структурная схема

Из схемы следует, что на выходе интегратора (s^{– 1}) формируется вектор состояния х. Матрица A называется основной матрицей системы. B – матрица связи вектора входа системы с переменными состояния. C – матрица связи переменных состояния с вектором выхода системы. D – матрица связи вектора входа с вектором выхода.