Укрупнені переходи трирівневого пристрою пам'яті
хі |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A27 |
A28 |
A29 |
A30 |
A31 |
A32 |
A33 |
A34 |
A35 |
A36 |
A37 |
A38 |
х1x5 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
A21 |
A22 |
х1x6 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
A23 |
A24 |
х1x7 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
A25 |
A26 |
х2x5 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
A27 |
A28 |
х2x6 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
A29 |
A30 |
х2x7 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
A31 |
A32 |
х3x5 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
A33 |
A34 |
х3x6 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
A35 |
A36 |
х3x7 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
A37 |
A38 |
х1 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
A21 |
A22 |
A23 |
A24 |
A25 |
A26 |
х2 |
A27 |
A28 |
A29 |
A30 |
A31 |
A32 |
A27 |
A28 |
A29 |
A30 |
A31 |
A32 |
A27 |
A28 |
A29 |
A30 |
A31 |
A32 |
х3 |
A33 |
A34 |
A35 |
A36 |
A37 |
A38 |
A33 |
A34 |
A35 |
A36 |
A37 |
A38 |
A33 |
A34 |
A35 |
A36 |
A37 |
A38 |
Трирівневий автомат А, як і дворівневий, здатний функціонувати в імовірнісному і нечіткому режимах [5-7].
Автомат А працює в імовірнісному режимі під впливом одного з імовірнісних слів pd(T), що складалися з пар вхідних сигналів х1, х2, х3, х5, х6, х7 автомата стратегії , якими встановлено відповідні стани Аj (табл. 3 і 4),.
Рис. 9. Закон роботи трирівневого пристрої пам'яті, як шести стійкого елемента в блоці е3 станів
і вхідного сигналу х11 керованої БФСП , який встановлює стан А11 (табл. 5), що не запам`ятовується, а також другого вхідного сигналу е(Δ).
Імовірнісні переходи в блоці πj станів представлені в табл. 7. Імовірнісний перехід здійснюється в один з двох станів цілком певних блоків πj (j= 4, 5, …, 12). Теоретична ймовірність переходу Pe в один зі станів πj рівна 0,5. На практиці воно коливається від 0 до 1 (1 ≥ Pe ≥ 0). При дослідженні імовірнісного переходу зазвичай він переходить в одне зі станів при Pe ≈ 0,3, а в інший стан - при Pe ≈ 0,7.
Таким чином, імовірнісні переходи забезпечують інтегрований перехід з певного стану аi в один зі станів певного блоку πj (j= 4, 5, …, 12).
У
розглянутому трирівневому
автоматі
А матричні
(нечіткі) переходи
представлені в табл.
8. Нечіткі
переходи
забезпечують
переходи
з довільного
стану Aj
в стан Ан
матричного
блоку
ei(Δ),
складається
з цілком визначених
блоків πi,
визначаються
дворівневим
автоматом
стратегії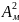
з
певною мірою
ймовірності Рн.
Таблиця 7