4.3. Метод множителей Логранжа

([8] - ст.166-171, [7] - ст.257-262;)

-------------------------------------------------- ---------------------------------------------

дано:

- Функции ограничений

g(x₀, x₁, x₂, …, x_n)= a_ijx_ij =b_іj (4.3.1)

- Целевая функция.

z= f(x₀, x₁, x₂, …, x_n) min(max) (4.3.2)

Найти: f(x_і) для которых z=С_ijx_ij min(max).

              Чтобы найти решение задачи вводят набор переменных _1,_2,...,n, которые называют множителями Лагранжа, а затем составляют функцию Лагранжа

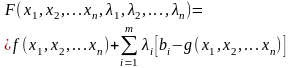                          (4.3.3)

              После этого находят частные производные

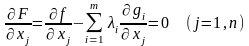                             (4.3.4)

и

                            (4.3.5)

              Затем решают систему с(m + n) уравнений

                               (4.3.6)

              Всякое решение системы уравнений (4.3.6) определяет точку Х = (x_0,x_1,x_2,...,x_n), в которой может иметь место экстремум функции f(x₀, x₁, x₂, …, x_n)

              Итак, решив систему уравнений (4.3.6) получаем все точки, в которых функция (4.3.2) может иметь экстремальные значения. Дальнейшие исследования найденых точек проводят также, как и в случае безусловного экстремума.

              Таким образом, определение экстремальных точек методом множителей Лагранжа включает следующие этапы:

1. Составление функции Лагранжа;

2. Нахождение частных производных от функции Лагранжа по переменным х_і, _і и приравнивания их к нулю.

3. Решая систему (4.3.6) находят точки, в которых целевая функция задачи может иметь экстремум.

4. Вычисляют значение функции (4.3.2) в найденных точках.

              Метод множителей Лагранжа имеет ограниченное использование, ибо система (4.3.6), как правило, имеет несколько решений.

              Метод Лагранжа теоретически можно использовать и когда некоторые ограничения должны вид неровностей и их решения должны быть неотъемлемым. Вводя дополнительные переменные, ограничения-неравенства можно превратить в уравнение, причем на дополнительные переменные накладываются условные неотъемлемости.

 

Пример 3. По плану производства продукции завода необходимо изготовить 180 деталей. Эти детали могут быть изготовлены двумя технологическими способами. При производстве деталей І способом затраты равны Е₁=4х₁+х₁² а при изготовлении ІІ способом они равны Е₂=8х₂+х₂².

Определить, сколько деталей каждым способом необходимо изготовить, чтобы общие затраты на производство продукции были минимальными.

 

Решение

 

              Математическая постановка задачи состоит в определении минимального значения функции

f= 4х₁+х₁²+8х₂+х₂² (1)

при условиях

х₁+х₂=180 (2)

х₁, х₂  0 (3)

              Задачу решаем методом множителей Лагранжа.

 

1. Составим функцию Лагранжа

2. F(x₁, x₂, )= 4х₁+х₁²+8х₂+х₂²+(180-x₁-x₂), (4)

 

2. Вычислим частные производные по x_1,x_2,  и приравняем их к нулю:

(5)

3. Решения "связав систему уравнений (5) получаем

 

================================================== ==============

 

Пример 4

дано:

n - количество видов запчастей;

d- общая сумма денег, выделенная на закупку всех запчастей;

b_j- стоимостьj-ой детали,j= 1, ... n;

Y_j -необходимость в j-й детали. Необходимость имеет показательное закон распределения с параметром a j;

a_j - параметр показательного закона распределения нужностиj-ой детали;

C_j- прибыль, который будет получен в результате использования j-ой детали;

r_j- убытки, которые будут получены в результате отсутствия j -ой детали;

q_j-убытки, Которые будут получены в результате неиспользования j-ой детали.

Распределить деньги d так, чтобы общая прибыль была максимальной.

              Таблица 1 - Исходные данные.

i	aj	bj	Cj	Rj	qj	d	n
1	0,25	20	30	18	12	820	3
2	0,15	25	22	18	10
3	0,10	30	25	15	10

 

Решение 

1. обозначим

x_j - Сумма, которая выделяется на закупку j-ой детали,

x _j/b_j- количество купленных j-ых деталей.

 

2. Примем, что все переменные непрерывные.

 

3. определим:

-           Получаемый доход, Р;

-           убытки от отсутствия детали, З_1;

-           убытки от неиспользования детали, З_2.

Результаты сведем в таблицу 2.

Таблица 2 - прибыль от использования деталей.

интервал	Прибыль, Р	Убытки, З1	Убытки, З2
Yj< xj/bj	CjYj	0	qi(xj /bj- Yj)
Yj= xj/bj	Cj xj/bj	0	0
Yj> xj/bj	Cj xj/bj	ri(Yj -xj /bj)	0

 

4. Определим суммарный доход по j-й детали:

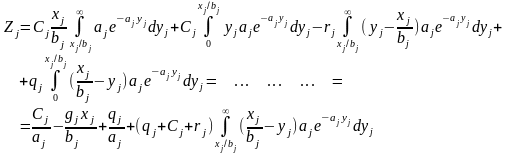4. (1)

 

5. Суммарная прибыль по n -Детали:

6. (2)

6. Математическая постановка задачи состоит в определении максимального значения функции

7. (3)

при условиях

или х₁+х₂+х₃ =820 (4)

х₁, х₂ , х₃  0 (5)

7. Задачу решим методом множителей Лагранжа.

Составляем функцию Лагранжа

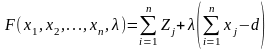(6)

8. Находим частные производные

, (7)

(8)

 

9. Вычислим частные производные по x _1, x _2,  и приравняем их к нулю получаем систему уравнений

10. (9)

12. (10)

10. : Решивши систему уравнений (…) получаем

11. х₁ = 120; х₂ = 250; х₃ = 450;

 

11. Найдем суммарную прибыль

Z₁ = 42.45; Z₂ = 38.95; Z₃ = 88.43;

 

Z₁ + Z₂ + Z₃ = Z₁ = 42.45 + 38.95 + 88.43 = 169.83 (единиц стоимости);