Р ис. 13.5 Гістограма частот

Графік F*(х) зображено на рис. 13.6.

Р ис. 13.6 Емпірична функція розподілу

З рис. 13.5 визначається модальний інтервал, який дорівнює 16 – 20. Застосовуючи формулу для обчислення моди і беручи до уваги, що , , , , , дістанемо:

З графіка F*(х) визначається медіанний інтервал, який дорівнює 12 - 16.

Беручи до уваги, що , і застосовуючи формулу для обчислення медіани, дістанемо:

Емпіричною функцією розподілу називають функцію,

де n_x – кількість варіант, які менші від x;

n – об’єм вибірки.

У табличній формі цей розподіл має такий вигляд:

h	x1 – x2	x2 – x3	x3 – x4	…	xk–1 – xk
ni	n1	n2	n3	…	Nk
Wi	W1	W2	W3	…	Wk

Тут h = x_i – x_i–1 є довжиною часткового i-го інтервалу. Як правило, цей інтервал береться однаковим.

Інтервальний статистичний розподіл вибірки можна подати графічно у вигляді гістограми частот або відносних частот, а також, як і для дискретного статистичного розподілу, емпіричною функцією F ^*(x) (комулятою).

Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і висотy .

Гістограма відносних частот є фігурою, що складається з прямокутників, кожний з яких має основу завдовжки h і висоту, що дорівнює .

1. Ряди статистичного розподілу та їхні форми

Задача математичної статистики полягає в розробці методів збору й обробки статистичних даних для отримання наукових і практичних висновків.

Генеральною сукупністю називається множина всіх можливих значень випадкової величини:

Одержані в результаті n експериментів числа : - вибіркою з цієї сукупності. Вибірка може записуватися у вигляді варіаційного або статистичного ряду.

Варіаційним рядом вибірки : називається послідовність варіант, записаних в порядку зростання. Різниця між максимальним і мінімальними елементами вибірки називається розмахом вибірки: .

Нехай у вибірці обсягу n елемент х_і зустрічається n разів.

Число n називається частотою елемента х_і . .

Статистичним рядом називається послідовність пар ( , ), тобто перелік варіант і відповідних їм частот. Записують статистичний ряд у вигляді таблиці, перший рядок якої містить елементи х_і , а другий – їх частоти n .

Приклад 1. Записати у вигляді варіаційного і статистичного рядів вибірку 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4. Знайти розмах вибірки.

Розв’язання

Обсяг вибірки n=15. Варіаційний ряд: 2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7,10, 10.

Розмах вибірки =10-2=8.

хі	2	3	4	5	7	10
	3	1	2	3	4	2

Статистичний ряд:

Приклад 2. Побудувати полігон і гістограму частот вибірки, випадково вибраних робочих заводу, якщо число інтервалів m=5 (вік робочих в роках):24, 19, 38, 25, 44, 52, 69, 47, 29, 34, 42, 31, 25, 28, 57, 40, 42, 61, 35, 47.

Розв’язання

=19; =69. Розмах вибірки Ширина інтервалів h=

Інтервал віку
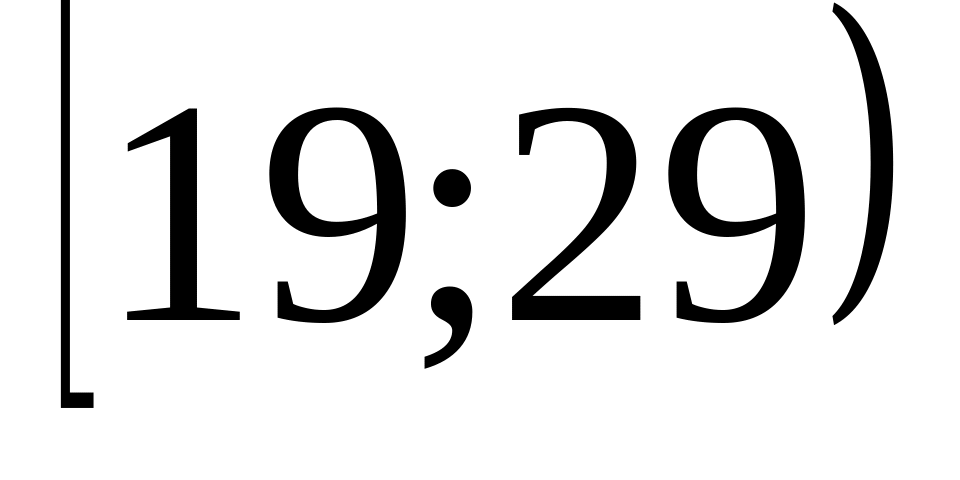
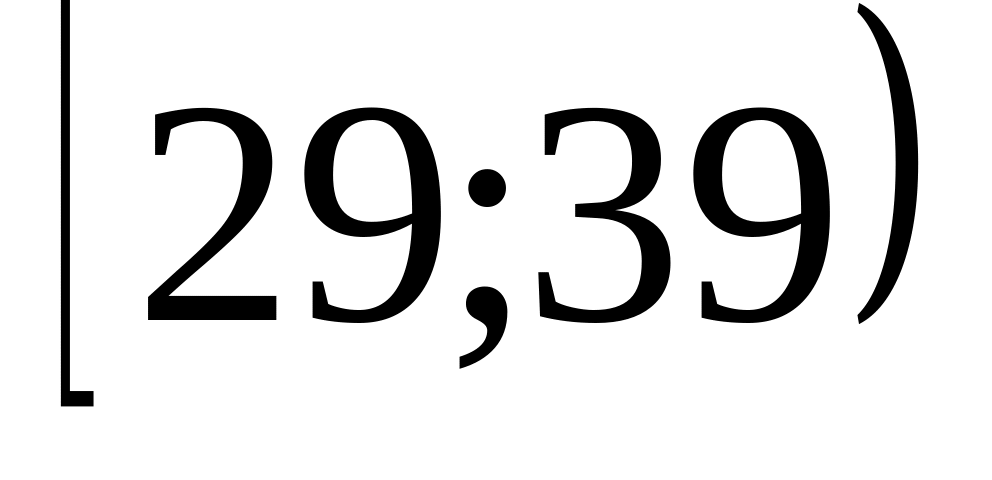
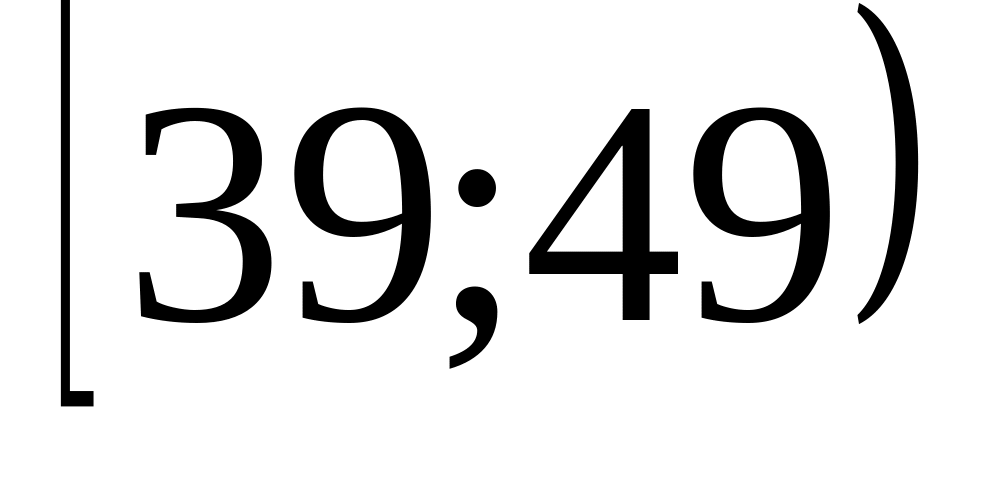
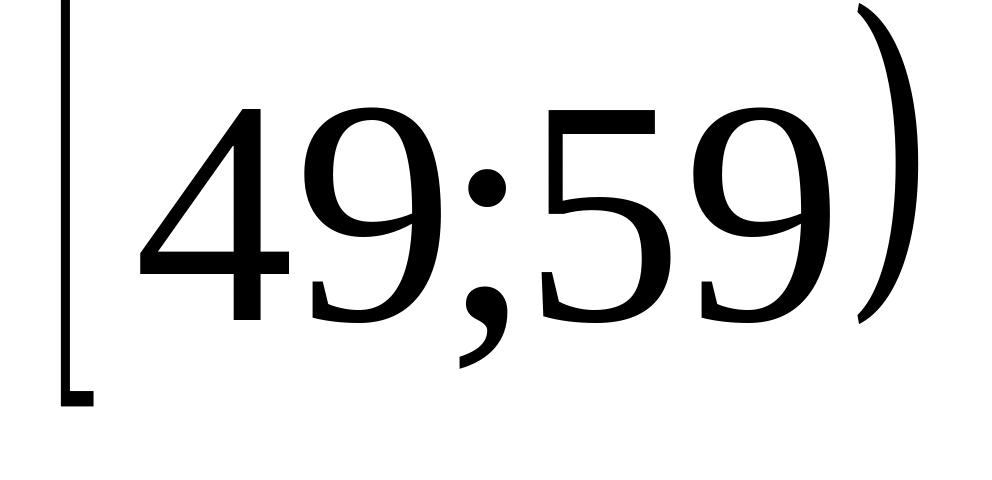
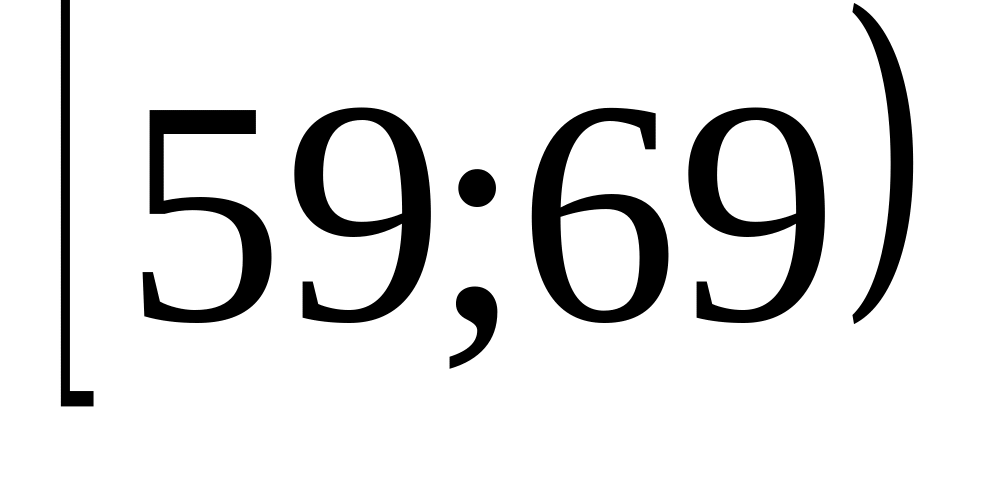
n	6	4	6	2	2
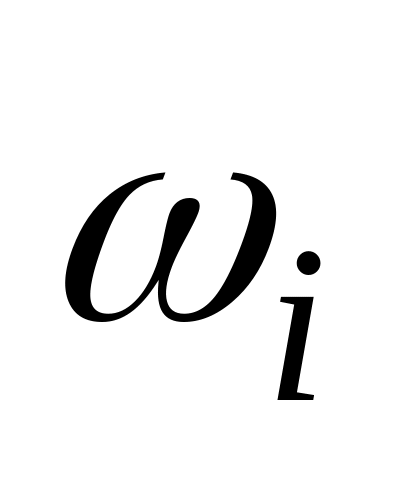
	0,3	0,2	0,3	0,1	0,1

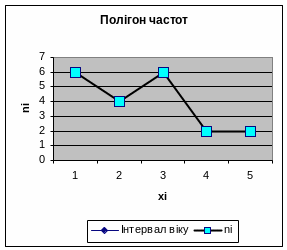
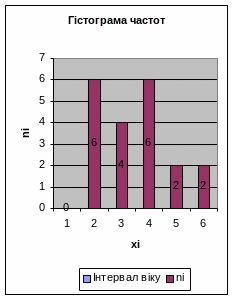
Приклад 3. Побудувати графік емпіричної функції розподілу числа очок, вибитих стрілком: 10, 10, 9, 10, 7, 9, 10, 8, 9, 10, 10, 10, 10, 6, 8, 10, 9, 8, 10, 10.

Розв’язання

Статистичний розподіл

	6	7	8	9	10
	1	1	3	4	11

Функція розподілу