
- •Тестовые задания по математике
- •Найдите сумму матриц и :
- •Найдите сумму матриц и :
- •Найдите произведение матриц и :
- •Найдите произведение матриц и :
- •Укажите матрицу, обратную матрице :
- •Определитель матрицы равен:
- •Тема 6: область определения функции. Предел. Производная
- •Тема 8: элементы комбинаторики и теории вероятностей
Тестовые задания по математике
ТЕМА: МАТРИЦЫ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Найдите сумму матриц
 и
и
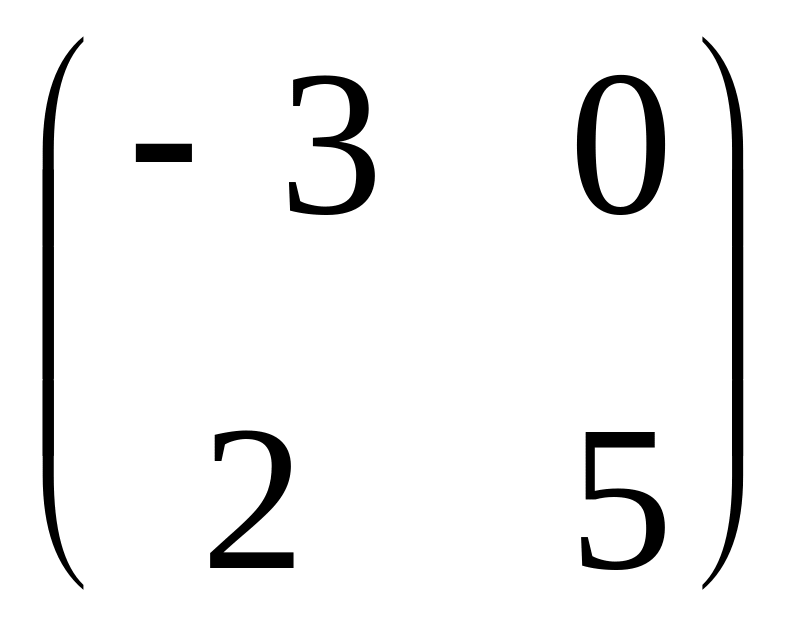 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Найдите сумму матриц и :
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Найдите сумму матриц и :
а)
 ;
;
б)
 ;
;
в)
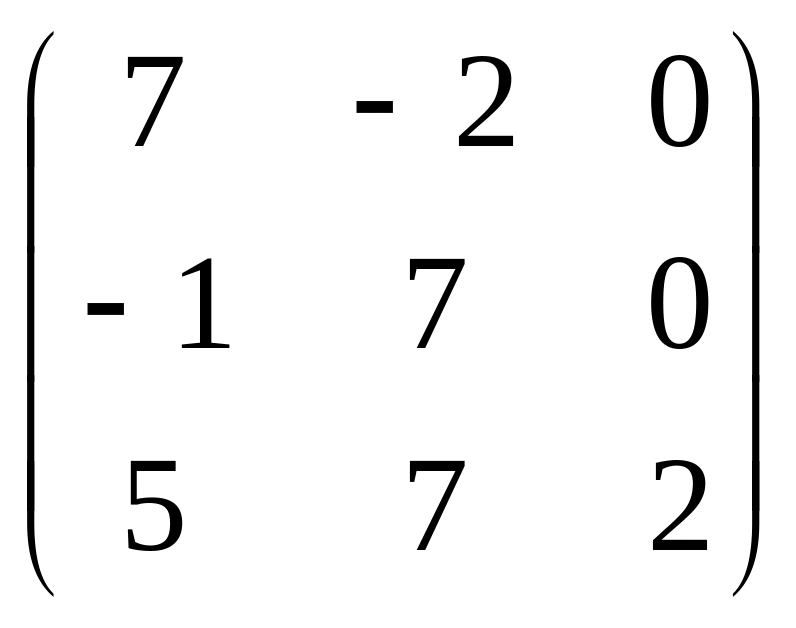 ;
;
г)
 .
.
Найдите матрицу 3А, если А =
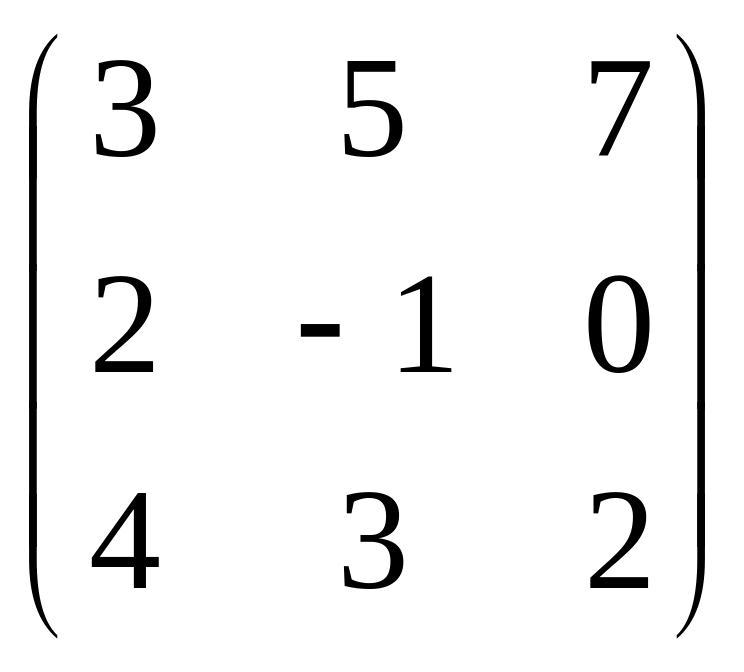 :
:
а)
 ;
;
б)
 ;
;
в)
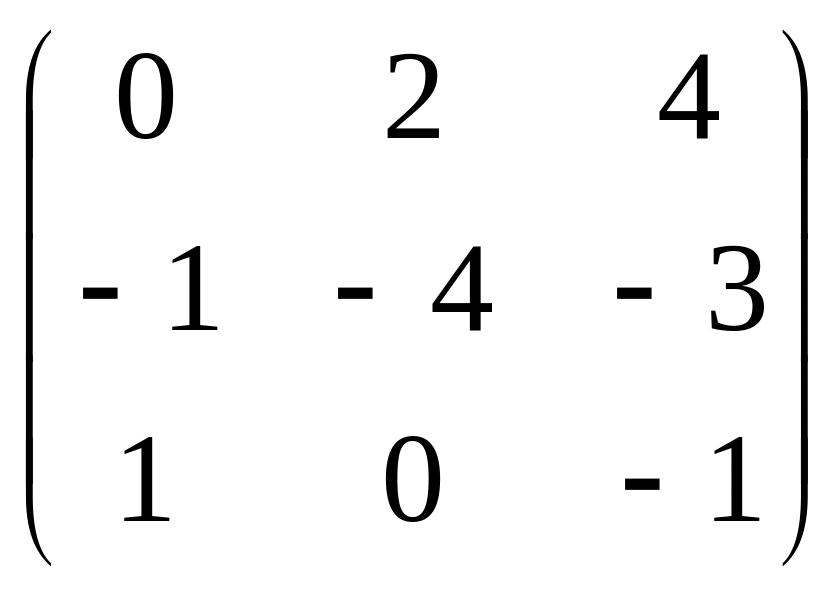 ;
;
г)
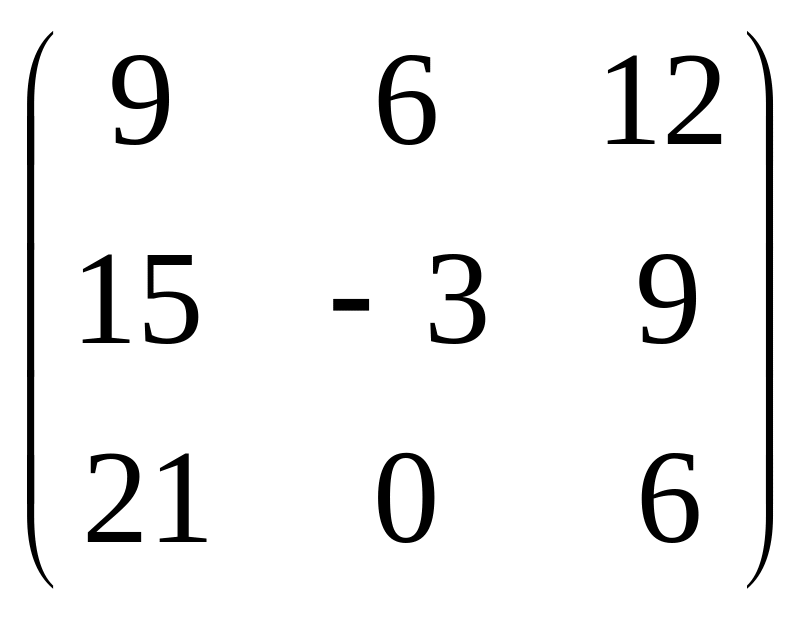 .
.
Найдите матрицу (–2)В, если В =
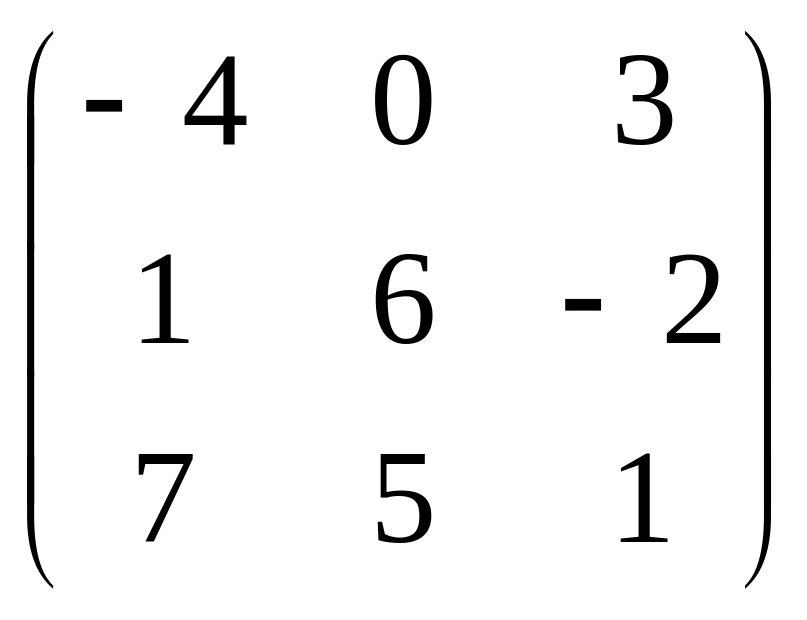 :
:
а)
 ;
;
б)
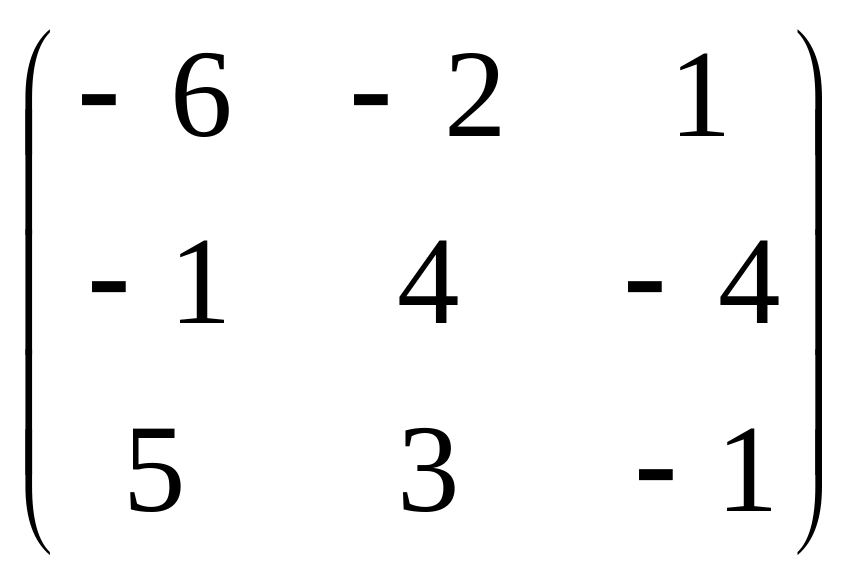 ;
;
в)
 ;
;
г)
 .
.
Найдите матрицу А + 2В, если А =
 ,
В =
,
В =
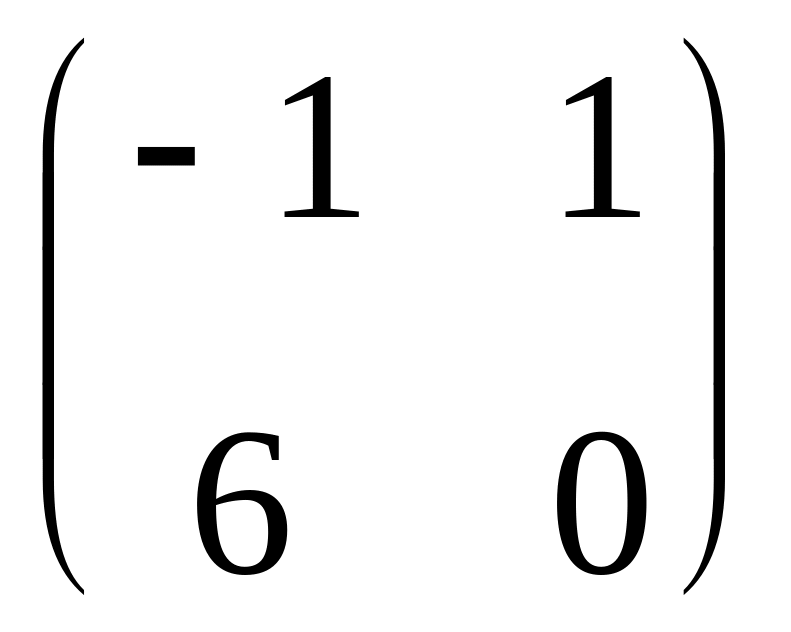 .
.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г) .
Найдите матрицу 4А – В, если А =
 ,
В =
,
В =
 .
.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Найдите произведение матриц
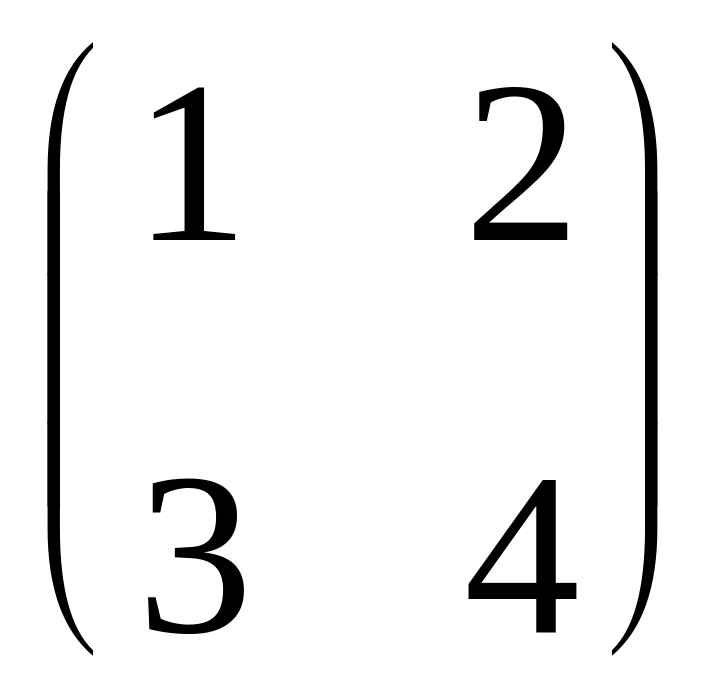 и
и
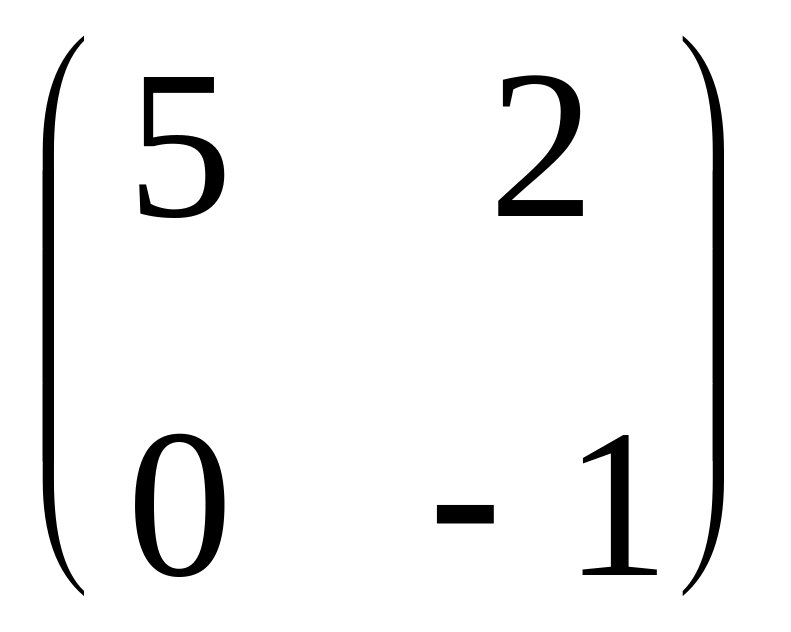 :
:
а)
![]() ;
;
б)
![]() ;
;
в) ;
г) .
Найдите произведение матриц и :
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Найдите произведение матриц и :
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Укажите матрицу, обратную матрице
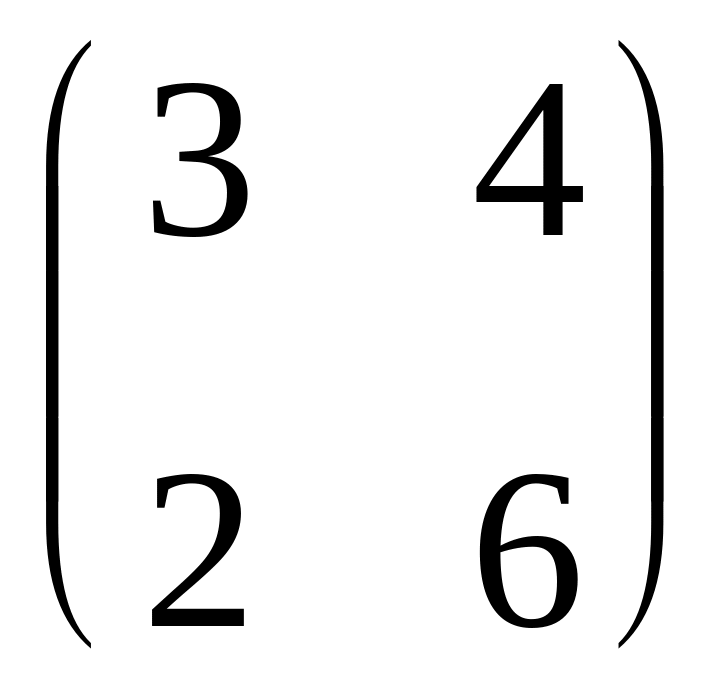 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
 .
.
Укажите матрицу, обратную матрице :
а)
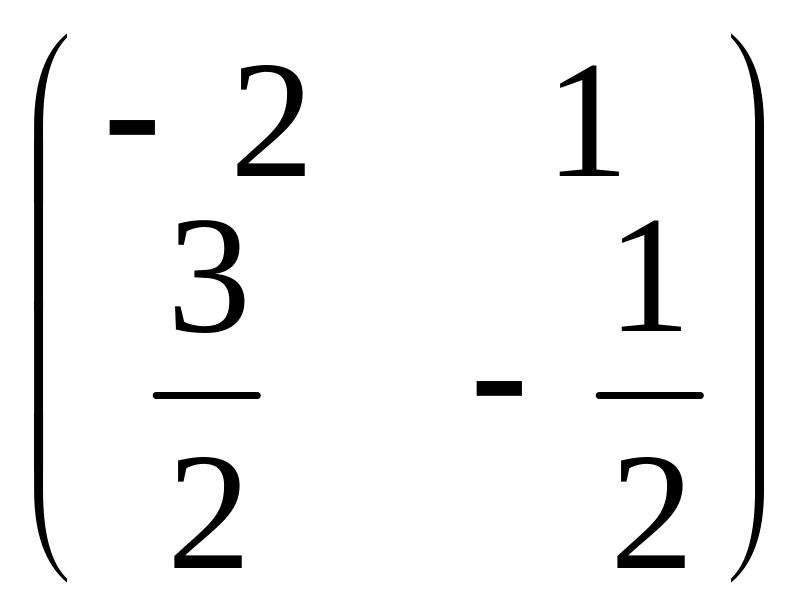 ;
;
б) ;
в)
![]() ;
;
г)
 .
.
Для матрицы
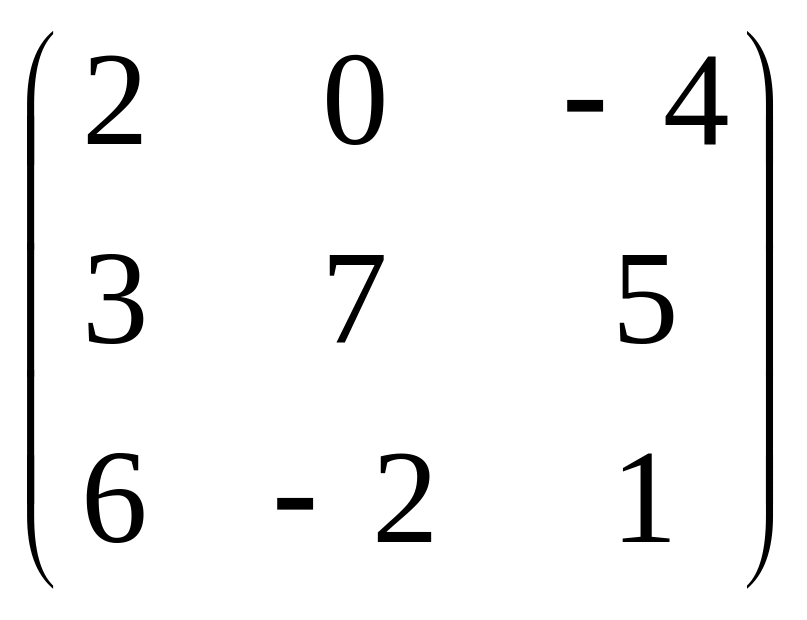 минор М33
равен:
минор М33
равен:
а) 28;
б) 14;
в) 12;
г) –48.
Для матрицы
 минор М12
равен:
минор М12
равен:
а) – 42;
б) 3;
в) 21;
г) –5.
Для матрицы
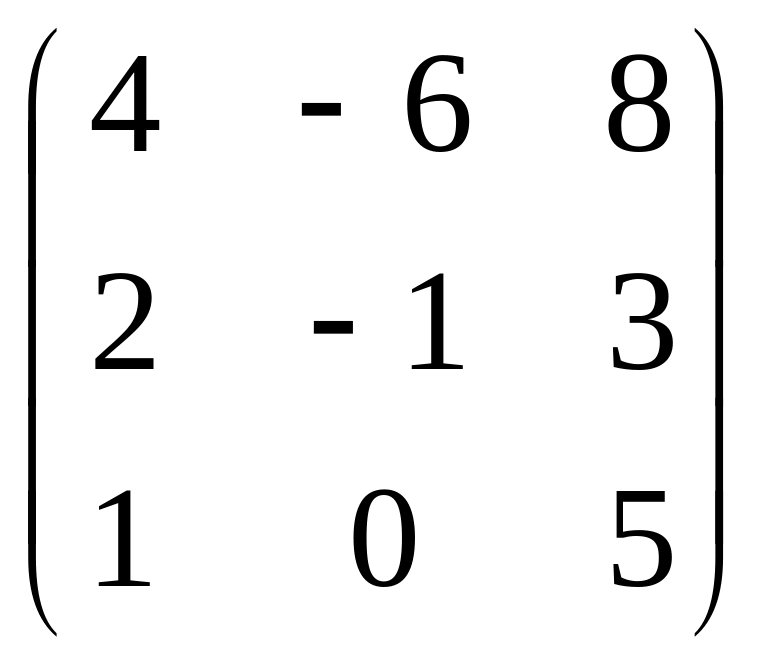 минор М22
равен:
минор М22
равен:
а) 8;
б) –1;
в) 18;
г) 12.
Для матрицы
 алгебраическое дополнение А11
равно:
алгебраическое дополнение А11
равно:
а) –3;
б) 1;
в) 3;
г) 0.
Для матрицы
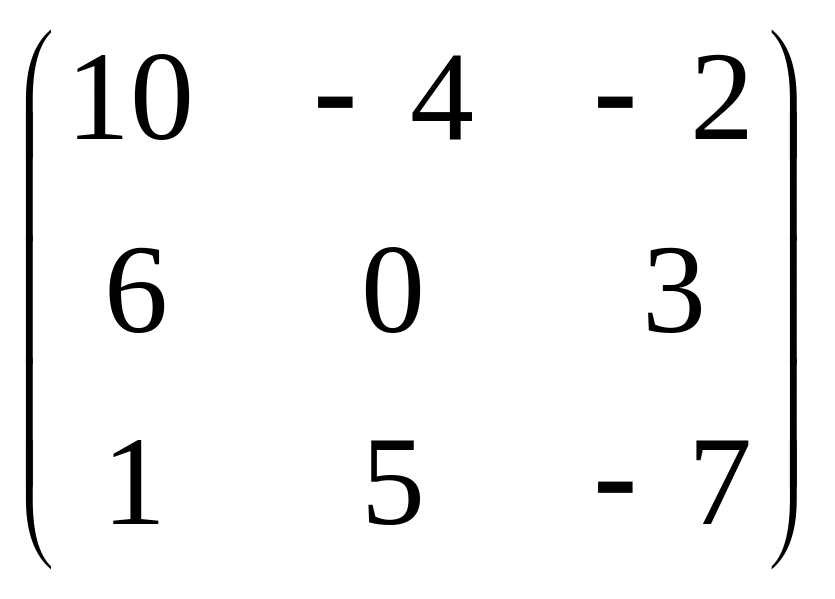 алгебраическое дополнение А13
равно:
алгебраическое дополнение А13
равно:
а) –2;
б) 30;
в) 12;
г) –30.
Для матрицы
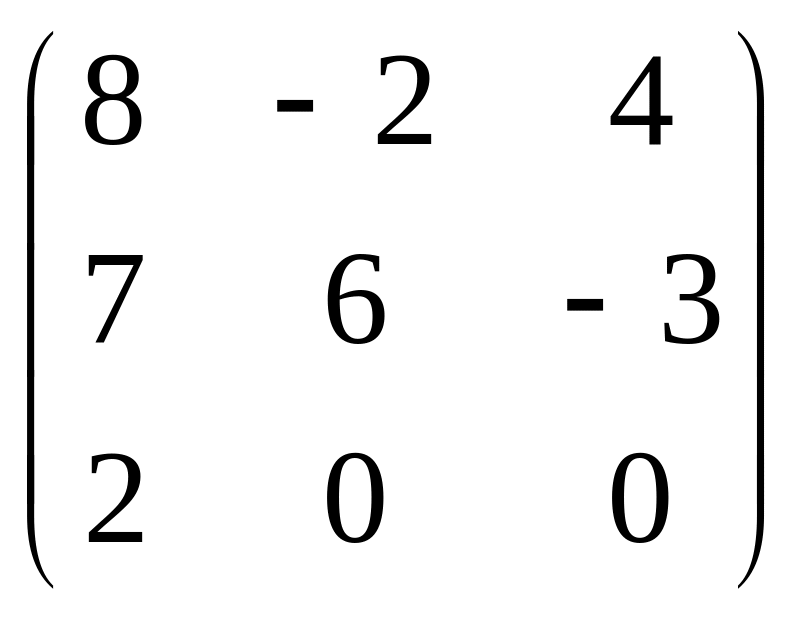 алгебраическое дополнение А21
равно:
алгебраическое дополнение А21
равно:
а) 2;
б) –2;
в) –7;
г) 0.
Определитель матрицы
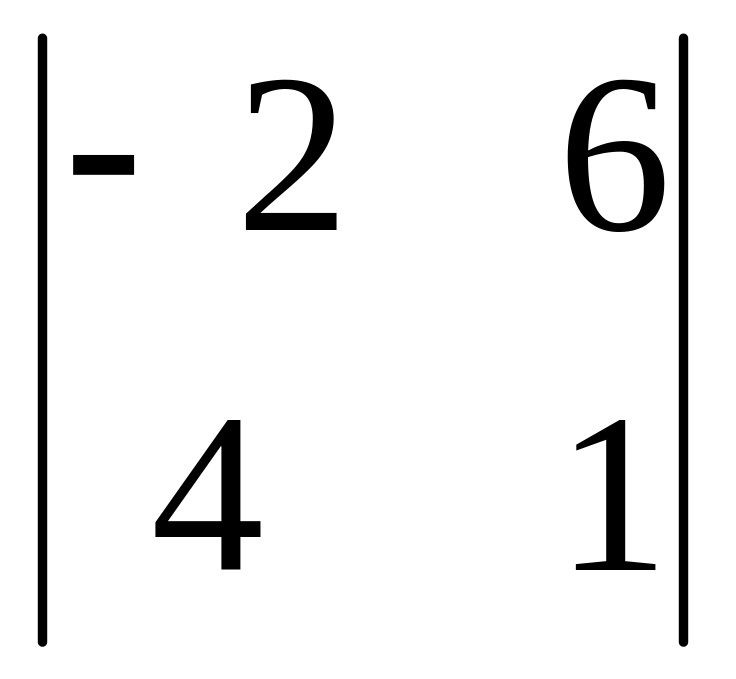 равен:
равен:
а) 9;
б) –26;
в) 22;
г) 0.
Определитель матрицы
 равен:
равен:
а) 15;
б) 93;
в) 42;
г) 54.
Определитель матрицы
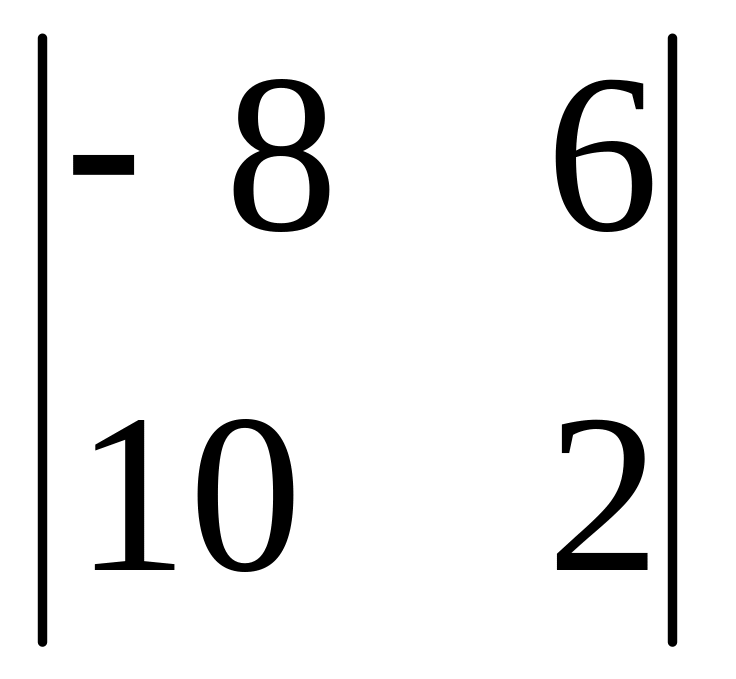 равен:
равен:
а) –76;
б) –40;
в) 12;
г) 25.
Определитель матрицы
 равен:
равен:
а) 0;
б) 2;
в) –8;
г) –1.
Определитель матрицы
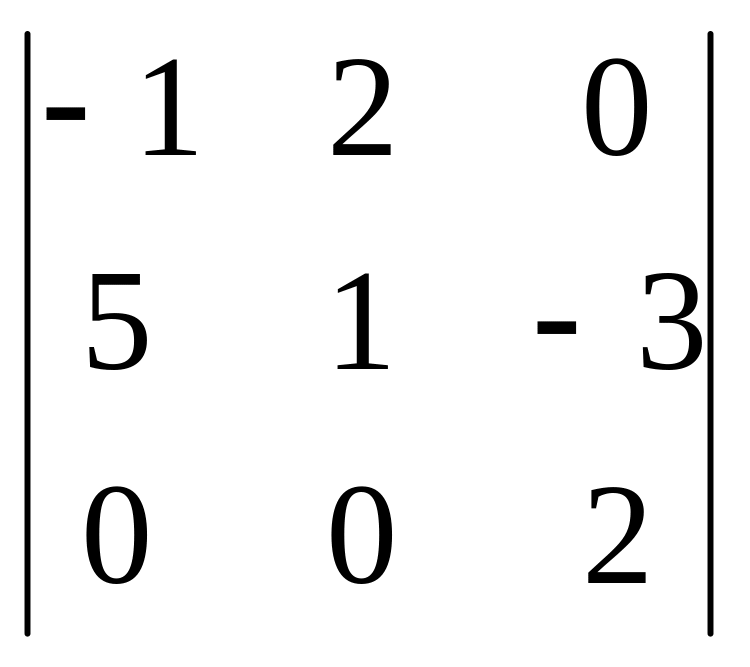 равен:
равен:
а) –22;
б) –10;
в) 0;
г) 4.
Для матрицы А =
 укажите Ат:
укажите Ат:
а)
 ;
;
б)
 ;
;
в)
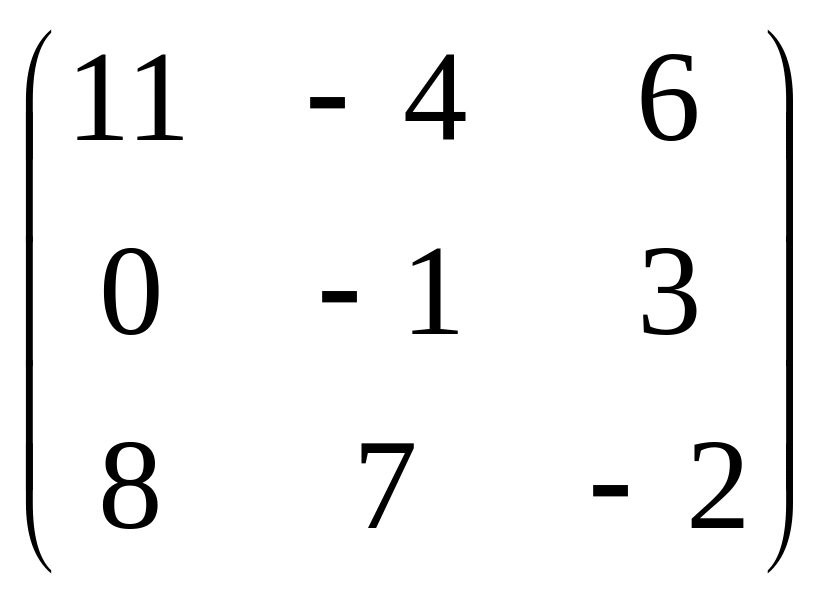 ;
;
г)
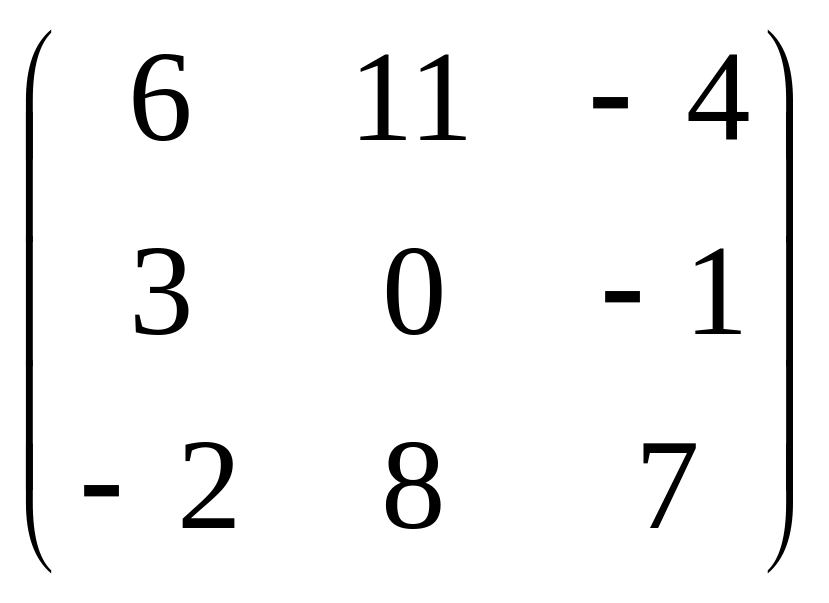 .
.
Для матрицы А =
 укажите Ат:
укажите Ат:
а) ;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Для матрицы А =
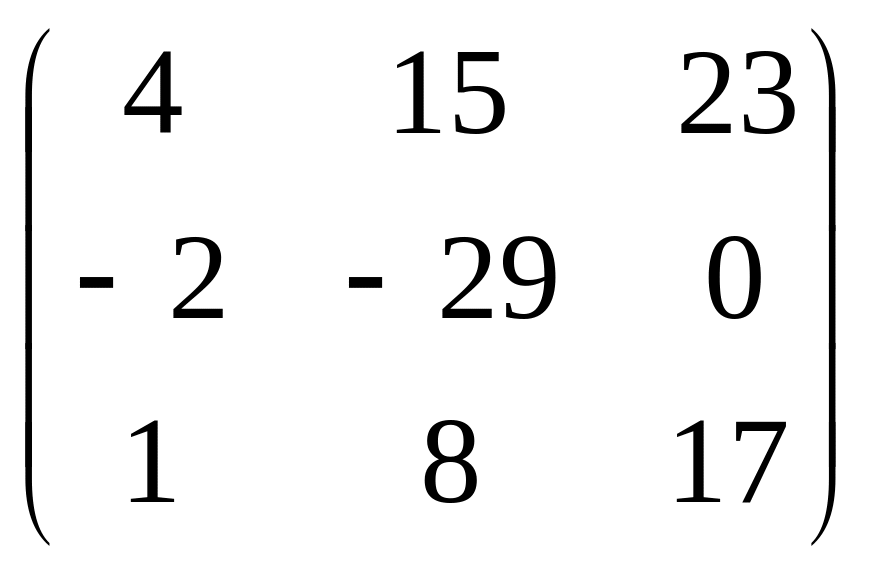 укажите Ат:
укажите Ат:
а)
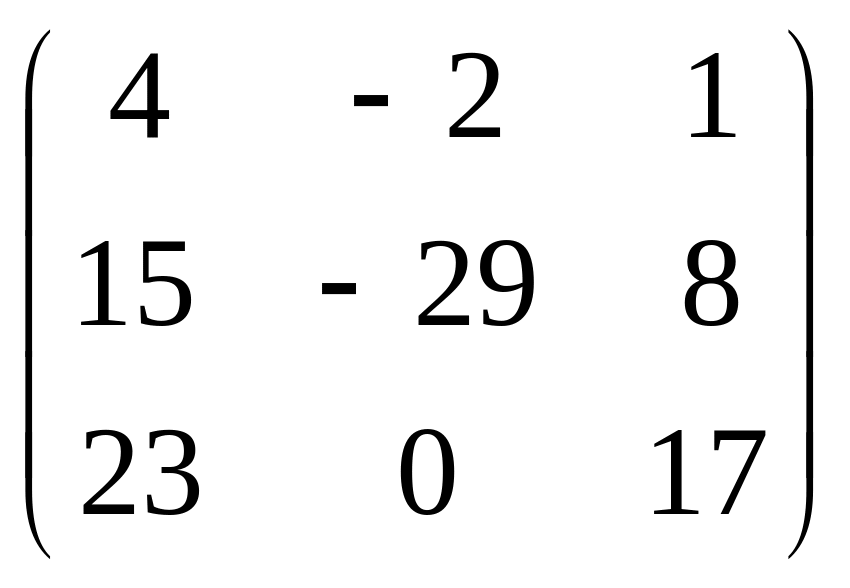 ;
;
б)
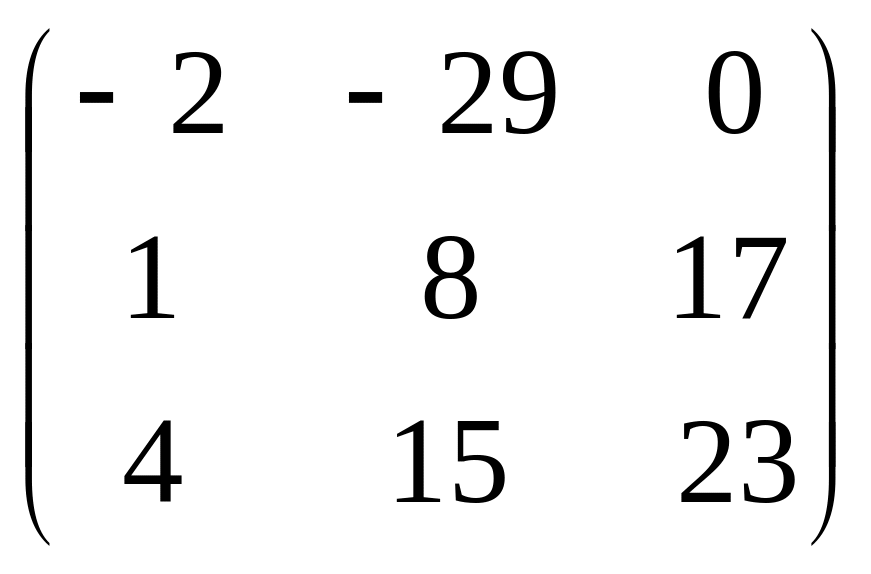 ;
;
в)
 ;
;
г)
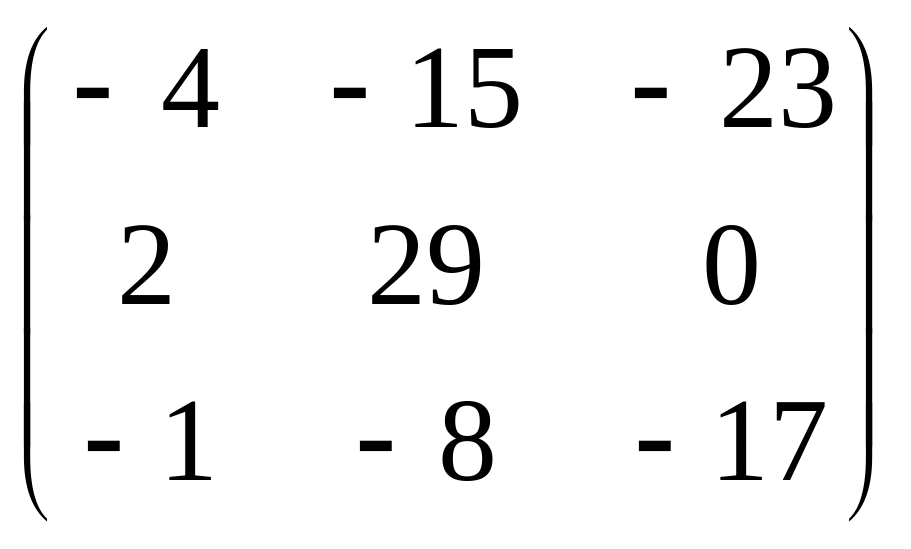 .
.
Найдите разность матриц
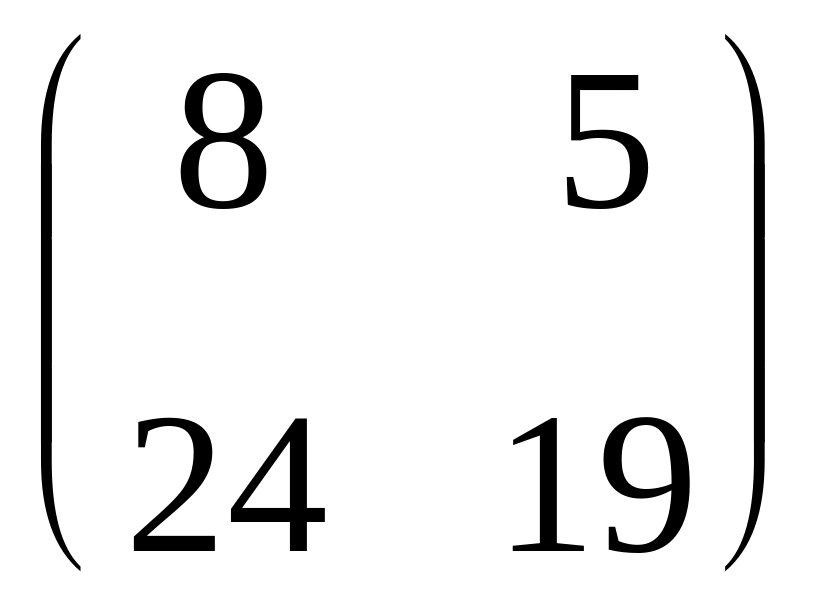 и
и
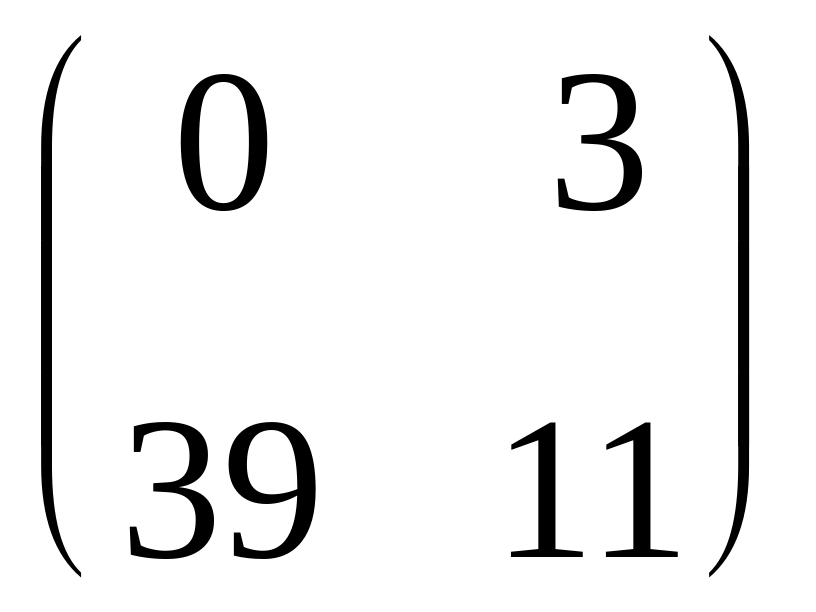 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Найдите разность матриц
 и
и
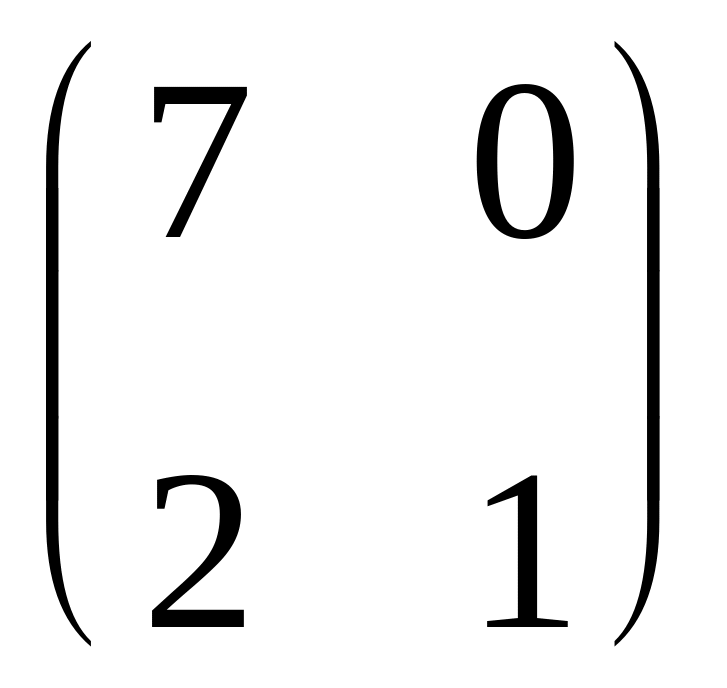 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Найдите разность матриц
 и
и
 :
:
а)
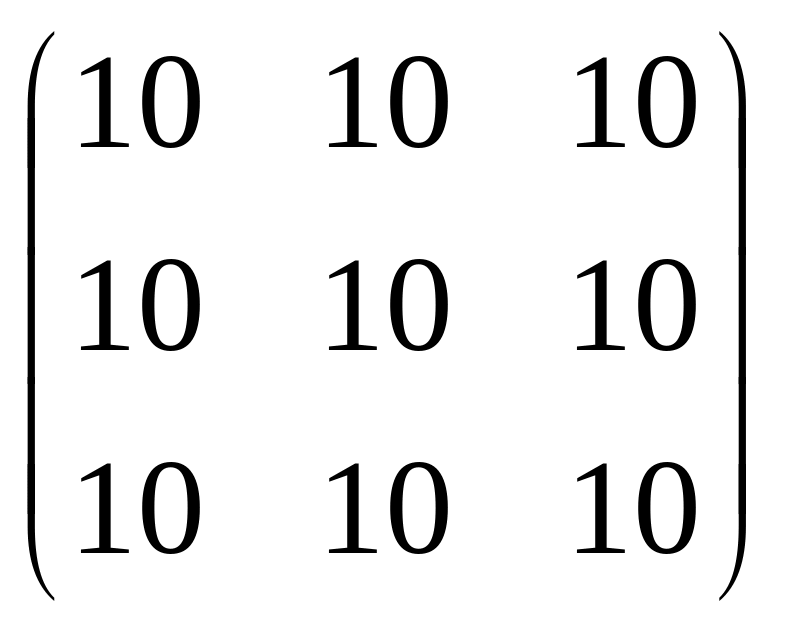 ;
;
б)
 ;
;
в)
 ;
;
г)
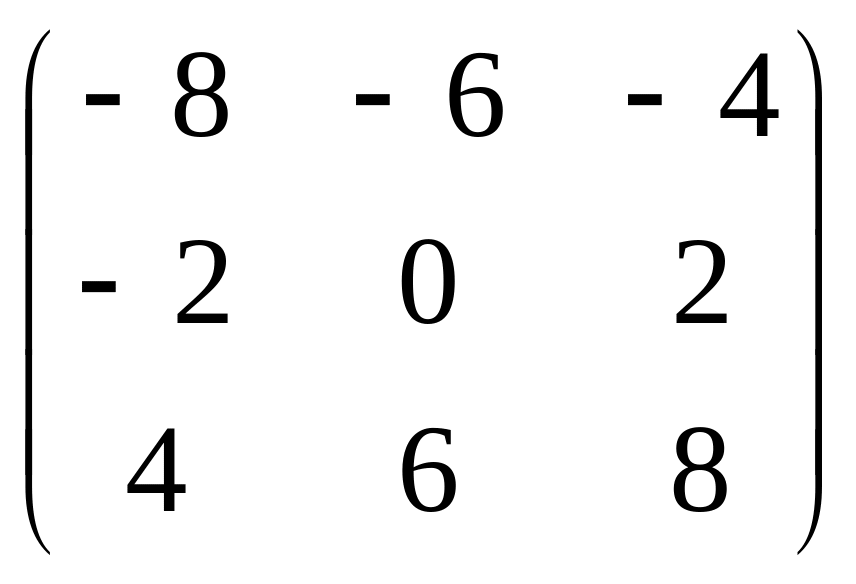 .
.
Укажите строчную матрицу:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Укажите столбцовую матрицу:
а) ;
б) ;
в) ;
г) .
Укажите порядок квадратной матрицы :
а) 0;
б) 1;
в) 2;
г) 3.
Укажите порядок квадратной матрицы
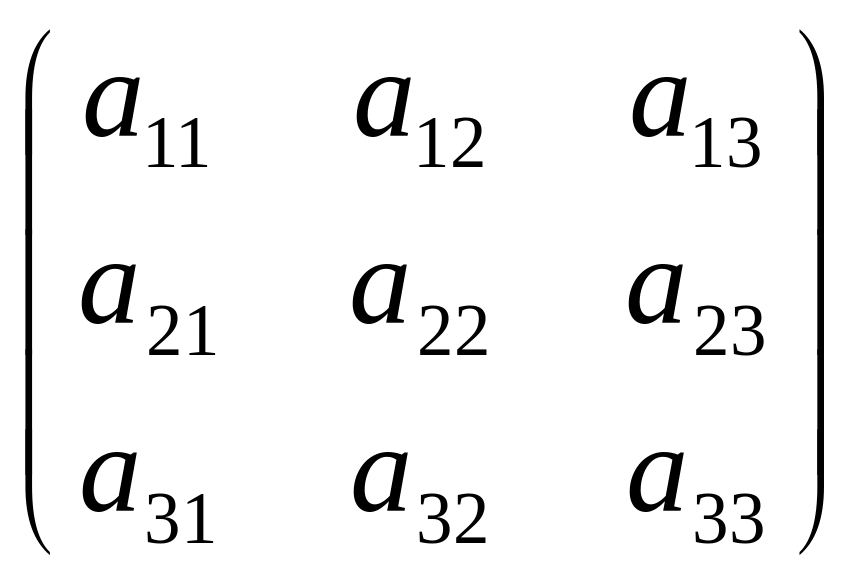 :
:
а) 1;
б) 2;
в) 3;
г) 4.
Укажите верное утверждение:
а) единичной называется квадратная матрица, у которой все элементы на главной диагонали равны 1;
б) диагональной называется квадратная матрица, у которой все элементы на главной диагонали равны 0;
в) нуль-матрицей называется матрица, все элементы которой равны нулю;
г) квадратной матрицей n-го порядка называется матрица размером n 2.
