Этап 2. Графическое решение стандартной злп

Построим область допустимых решений задачи (рисунок 3.9). Для построения градиента увеличим координаты вектора в 50 раз, получим . Перпендикулярно градиенту построим одну из линий уровня.

| |

Рисунок 4 – Графическое решение задачи о рационе

Передвигая линию уровня в направлении градиента, найдем точку входа в область допустимых значений – это точка . Для нахождения координат этой точки решим систему уравнений прямых ( ) и ( ), пересекающихся в точке : . Получим .

В точке целевая функция принимает наименьшее значение, равное .

Оптимальное решение , при котором

Этап 3. Анализ оптимального решения

Оптимальный рацион составляет 20 кг сена и 40 кг силоса, при этом себестоимость минимальная и составляет 56 ден. ед.

Подставив координаты оптимального решения в каждое неравенство, увидим, что третье и шестое неравенства обращаются в уравнения, а остальные – в строгие неравенства.

Это означает, что оптимальный рацион содержит необходимое количество кормовых единиц и фосфора, а белка и кальция – в избытке, причем сено и силос используются не в полном объеме.

Вопросы для самоконтроля

1. Запишите задачу линейного программирования в общей форме.

2. Запишите задачу линейного программирования в канонической и стандартной формах.

3. С помощью каких преобразований можно перейти от общей или стандартной формы задачи линейного программирования к канонической?

4. Дайте определение допустимого и оптимального решений задачи линейного программирования.

5. Какое из решени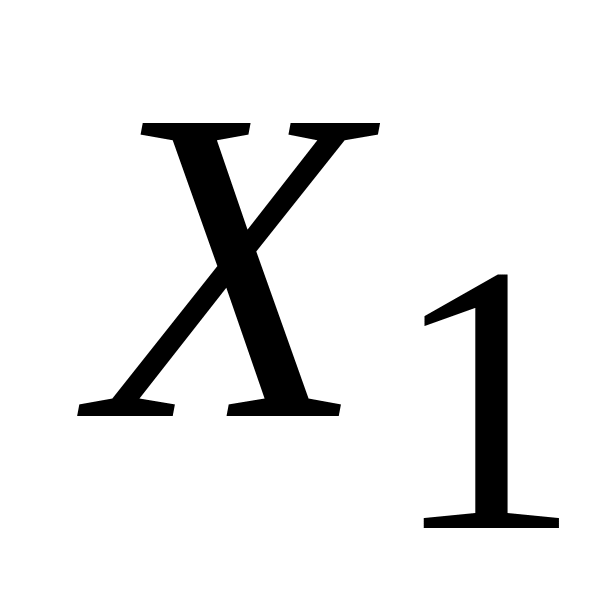й и 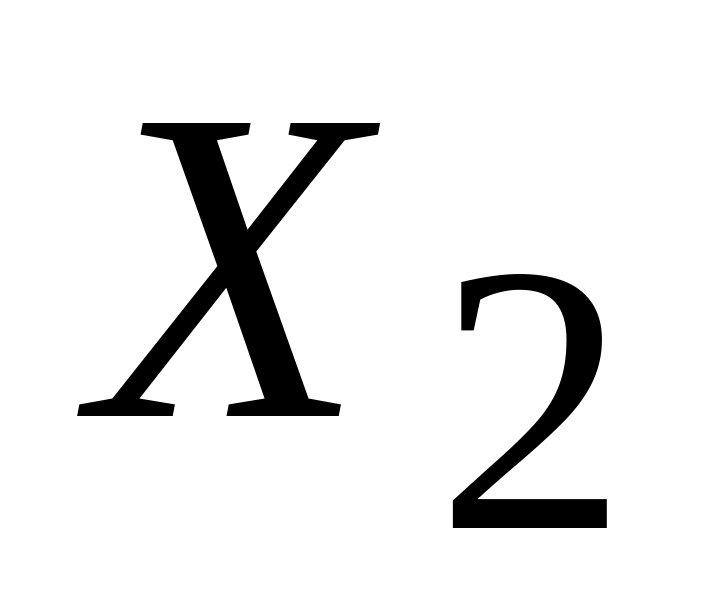является «лучшим» для задачи минимизации функции , если ?

6. Какое из решений и является «лучшим» для задачи максимизации функции , если ?

7. Запишите стандартную форму математической модели задачи линейного программирования с двумя переменными.

8. Как построить полуплоскость, заданную линейным неравенством с двумя переменными ?

9. Что называется решением системы 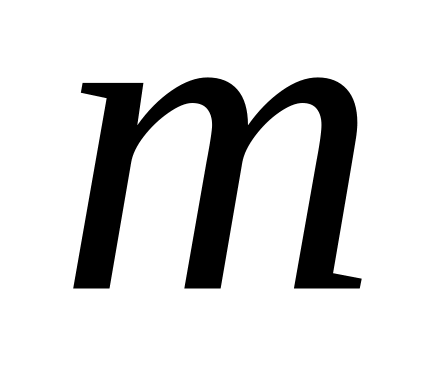линейных неравенств с двумя переменными? Постройте на плоскости область допустимых решений такой системы линейных неравенств, которая:

   1. имеет единственное решение;

   2. имеет бесконечное множество решений;

   3. не имеет ни одного решения.

10. Запишите для линейной функции 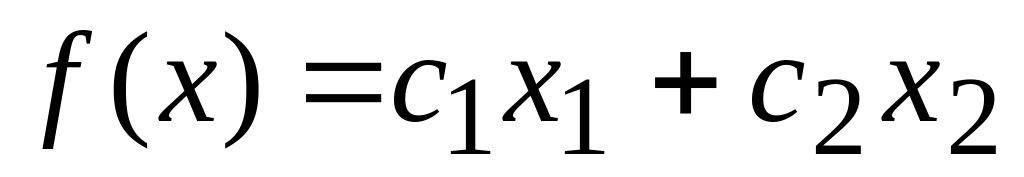вектор градиент, назовите вид линий уровня. Как расположены относительно друг друга градиент и линии уровня?

11. Сформулируйте алгоритм графического метода решения стандартной ЗЛП с двумя переменными.

12. Как найти координаты решения и значения , ?

13. Постройте область допустимых решений, градиент и линии уровня 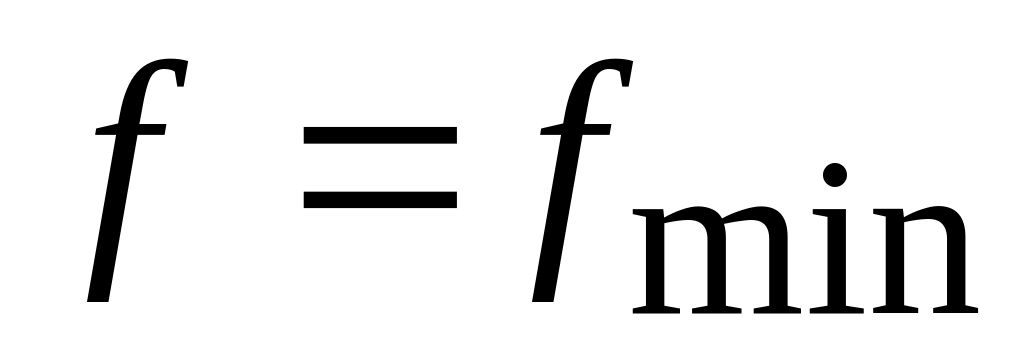, 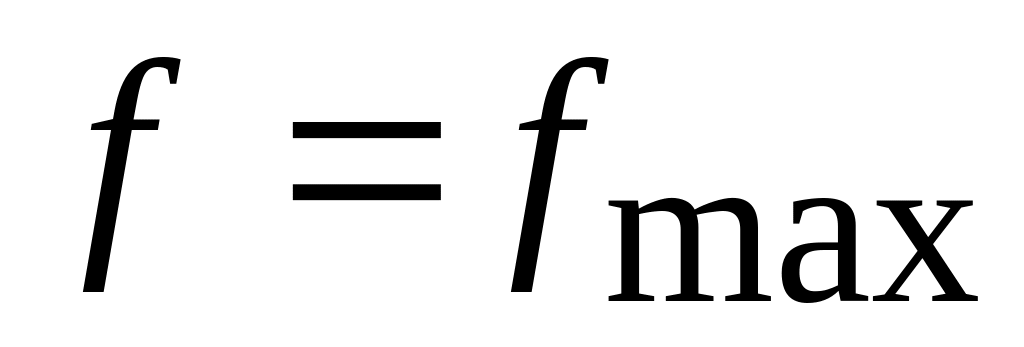для задач линейного программирования, в которых:

    1. достигается в единственной точке, а - на отрезке ОДР;

    2. достигается в единственной точке ОДР, а .

14. Дайте геометрическую иллюстрацию ЗЛП, если она:

    1. имеет единственные оптимальные решения для и ;

    2. имеет множество оптимальных решений для .

9