Лекция 2 графический метод нахождения оптимального решения

1. Формы линейных математических моделей и их преобразование

2. Графический метод решения задачи линейного программирования

3. Особые ситуации графического решения ЗЛП

4. Графическое решение экономических задач линейного программирования

1. Формы линейных математических моделей и их преобразование

Математическая модель задачи линейного программирования (ЗЛП) может быть записана в одной из трех форм.

В общей форме математической модели требуется найти максимум или минимум целевой функции; система ограничений содержит неравенства и уравнения; не все переменные могут быть неотрицательными.

В канонической форме математической модели требуется найти максимум целевой функции; система ограничений состоит только из уравнений; все переменные неотрицательны.

В стандартной форме математической модели требуется найти максимум или минимум функции; все ограничения являются неравенствами; все переменные неотрицательны.

Решение системы ограничений, удовлетворяющее условиям неотрицательности переменных, называют допустимым решением ЗЛП (допустимым планом).

Множество допустимых решений называют областью допустимых решений ЗЛП.

Допустимое решение , при котором целевая функция достигает экстремального значения, называют оптимальным решением ЗЛП.

Три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью математических преобразований может быть сведена к другой форме.

Необходимость перехода от одной формы математической модели к другой связана с методами решения задач: например, симплексный метод, широко используемый в линейном программировании, применяется к задаче, записанной в канонической форме, а графический метод – к стандартной форме математической модели.

Переход к канонической форме записи ЗЛП.

Пример.

Запишем задачу в канонической форме, вводя в левую часть первого неравенства системы ограничений дополнительную (балансовую) переменную со знаком «+», а в левую часть второго неравенства дополнительную переменную со знаком «минус».

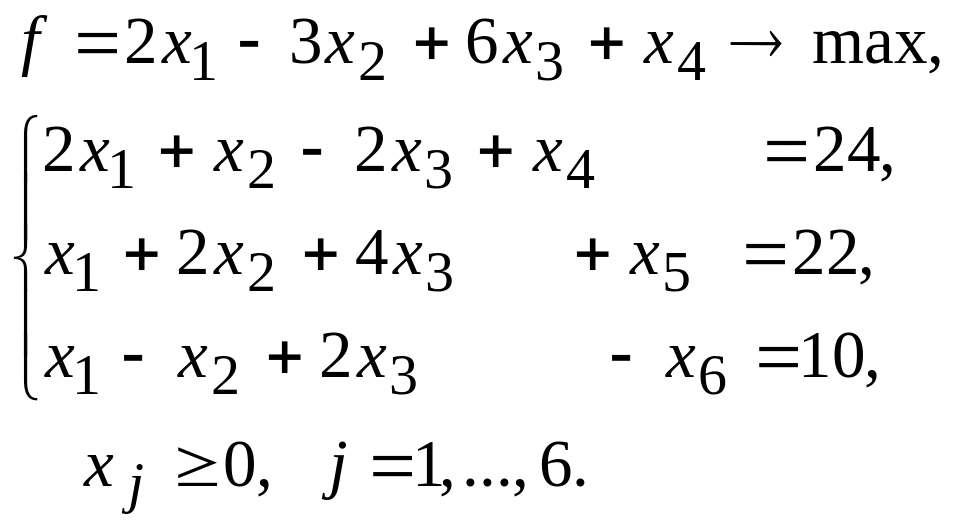
Экономический смысл различных дополнительных переменных может быть не одинаков: он зависит от экономического смысла ограничений, в которые эти переменные входят.

Так, в задаче об использовании сырья они показывают остаток сырья, а в задаче о выборе оптимальных технологий – неиспользованное время работы предприятия по определенной технологии; в задаче о раскрое – выпуск заготовок данной длины сверх плана и т.п.

2. Графический метод решения задачи линейного программирования

Графический метод применяется для решения задачи линейного программирования с двумя независимыми переменными:

найти наибольшее и наименьшее значения функции

при ограничениях

.

При использовании графического метода применяются линии уровня и градиент.

Для линейной функции координатами градиента являются коэффициенты при переменных и : . Градиент показывает направление возрастания целевой функции.

Линией уровня функции называется множество всех точек , в которых значение функции постоянно . Для линейной функции все линии уровня являются прямыми, перпендикулярными градиенту.

Решение системы линейных неравенств (3.2) называется допустимым, если его координаты неотрицательны , .

Множество допустимых решений системы линейных неравенств называется областью допустимых решений.

Область допустимых решений системы линейных неравенств расположена в первой четверти координатной плоскости.

Геометрическая постановка ЗЛП с двумя переменными: найти в области допустимых решений задачи точку, через которую проходит линия уровня (или ), соответствующая наибольшему (наименьшему) значению целевой функции .

Приведем алгоритм графического метода решения задачи линейного программирования (ЗЛП).

1. Построить область допустимых решений (ОДР) задачи в соответствии с системой неравенств .

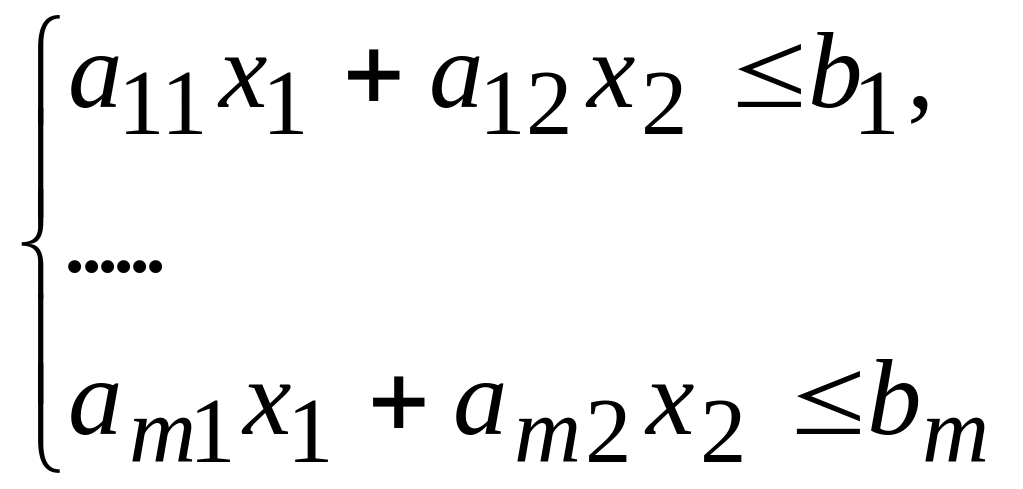2. Если область допустимых решений непустая, то можно говорить о целесообразности нахождения оптимального решения ЗЛП.

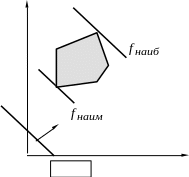
В

A

Рисунок 1 – Графический метод решения задачи

3. Строим для целевой функции градиент и фиксированную линию уровня – прямую .

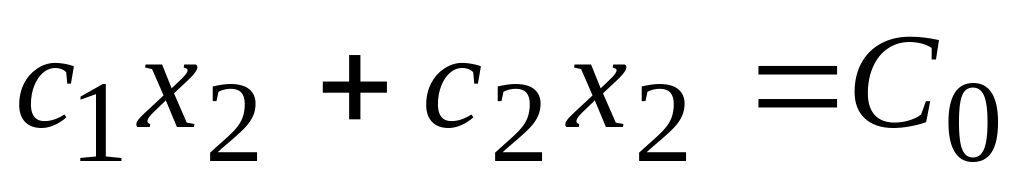4. Параллельным перемещением прямой 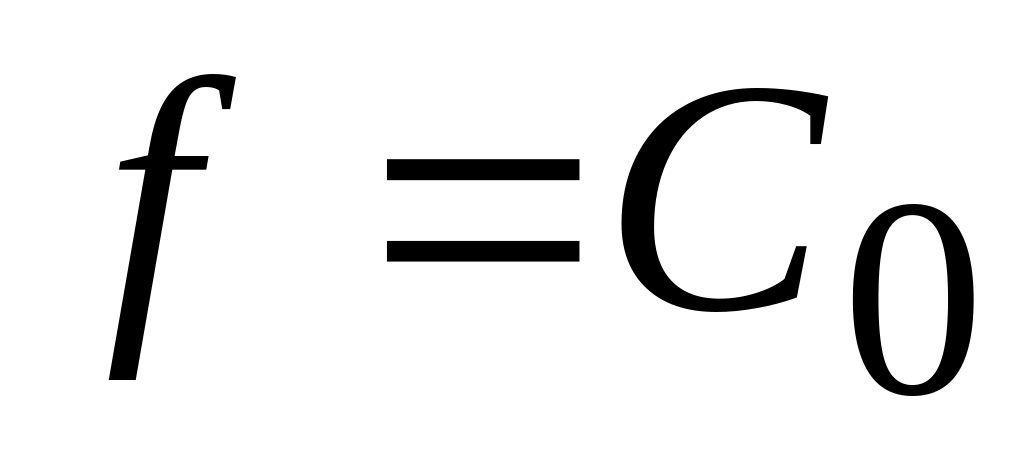в направлении вектора найдем первую точку «встречи» прямой с областью. Это – точка минимума целевой функции . Значение функции является наименьшим значением функции в ОДР.

5. Найдем последнюю точку встречи прямой с ОДР. Это - точка максимума целевой функции . Значение функции является наибольшим значением целевой функции в области допустимых решений.