Методические указания по выполнению контрольной работы № 1

Для решения задач № 1 – 6 требуется усвоить основные понятия, характеризующие электрическое поле: напряженность, потенциал, напряжение, диэлектрическая проницаемость.

Напряженность в заданной точке электрического поля, созданного несколькими зарядами, определяется по принципу суперпозиции (наложения), т.е. напряженность поля равна геометрической сумме напряженностей от каждого заряда в отдельности.

Величина напряженности поля заряда в заданной точке определяется по формуле:

E = , где ε_о = 8,85·10^-12 Ф/м - электрическая постоянная; Q – заряд тела, Кл; ε - относительная диэлектрическая проницаемость среды; R – расстояние от заряда до точки.

Если угол между векторами Е₁ и Е₂ прямой, то напряженность поля в заданной точке находится по теореме Пифагора:

Е = √ Е₁² + Е₂²

Величину напряженности поля в заданной точке можно определить и графически: отложить в выбранном масштабе векторы Е₁ и Е₂; геометрическим сложением векторов

Е₁ и Е₂ получить вектор Е; измерить длину вектора напряженности Е и умножить её на масштаб: Е = ℓ_Е ^. М_Е.

Потенциал поля точечного заряда: φ = Q/4·π·ε_о·ε·R

Если поле образовано несколькими точечными зарядами, то потенциал поля в заданной точке равен алгебраической сумме потенциалов полей, образованных в этой точке каждым зарядом отдельно: φ = ∑φ_i

Пример 1. Два точечных заряда 6,7 нКл и -13,3 нКл находятся на расстоянии 5 см друг от друга. Определить напряженность и потенциал электрического поля в точке, расположенной на расстоянии 3 см от положительного заряда и 4 см от отрицательного.

Дано: Q₁ = 6,7 нКл = 6,7 ^.10^-9 Кл; Q₂ = -13,3 нКл = -13,3 ^.10^-9 Кл;

R = 5 см = 5^.10^-2 м; R₁ = 3 см = 3^.10^-2 м; R₂ = 4 см = 4^.10^-2 м.

Решение.

1. Так как заряды точечные, то напряженности поля, созданного каждым зарядом:

E₁ = Q₁/ (4π·εo·ε·R₁²) = 6,7^.10^-9.9^.10⁹/1^.(3^.10^-2)² = 67^.10³ В/м;

E₂ = Q₂/ (4π·εo·ε·R₂²) = 13,3^.10^{-9 .} 9^.10⁹/1^.(4^.10^-2)² = 74,8^.10³ В/м.

2. Из условия задачи следует, что угол между векторами Е₁ и Е₂ прямой, тогда напряженность поля в точке А находим по теореме Пифагора:

Е = = ==101000 В/м = 101 кВ/м.

Величину напряженности поля в т. А можно определить графическим методом.

3. Потенциал электрического поля в т. А:

= = Q₁/ (4π·εo·ε·R₁) + Q₂ /(4π·εo·ε·R₂) = 9^.10^{9 .} (Q₁/R₁ + Q₂/R₂) =

= 6,7^.10^-9/3^.10^-2 - 13,3^.10^-9/4^.10^-2 = 9^.10^9.10^-7(6,6/3 - 13,3/4) = - 919,8 В.

Для решения задач № 7 – 12 необходимо изучить материал «Электрическая ёмкость и конденсаторы».

Нередко возникает необходимость соединять имеющиеся конденсаторы в батареи последовательно, параллельно и смешанно, подбирая конденсаторы по ёмкости и напряжению. Для решения задач необходимо усвоить принципы распределения напряжения и заряда в схемах последовательного и параллельного соединения конденсаторов; знать формулы эквивалентной ёмкости и энергии электрического поля конденсаторов.

В учебном пособии Частоедова рассмотрен пример расчета цепи смешанного соединения конденсаторов.

Рассмотрим пример задачи, когда известно напряжение на одном из конденсаторов.

Пример 2. На рис. 7 приведена схема соединения конденсаторов. Определить эквивалентную ёмкость С_экв батареи конденсаторов; общий заряд Q; напряжение сети U, напряжение и заряд на каждом конденсаторе, если известно: С₁ = 24 мкФ; С₂ = С₃ = 8 мкФ; С₄ = 12 мкФ; С₅ = 6 мкФ; напряжение на пятом конденсаторе U₅ = 30 В.

+ •

C₁ C₂ C₄

U C₃ C₅ Рис. 7

- •

Дано: С₁ = 24 мкФ; С₂ = С₃ = 8мкФ; С₄ = 12 мкФ; С₅ = 6 мкФ; U₅ = 30 В.

Определить: U - ?; Q - ?; C - ?; U₁ - ?; U₂ - ?; U₃ - ?; U₄ - ?; Q₁ - ?.

Решение:

1. Общая ёмкость последовательного соединения конденсаторов С₄ и С₅:

С₄,₅ = С₄^.С₅ / (С₄ + С₅) = 12 ^. 6 / (12 + 6) = 4 мкФ.

2. Общая ёмкость параллельно соединенных конденсаторов С₃ и С₄,₅:

С₃-₅ = С₃ + С₄,₅ = 8 + 4 = 12 мкФ.

3. Общая ёмкость последовательно соединённых конденсаторов С₁, С₂ и С₃-₅, которая и является эквивалентной ёмкостью батареи конденсаторов:

4. По заданному напряжению U₅ и ёмкости конденсаторов С₅ определяем заряд, накапливаемый этим конденсатором:

U₅ = С₅^.U₅ = 6^.10^-6.30 = 180^.10^-6 Кл.

5. Заряд конденсатора С₄ равен Q₄ = Q₅ = Q₄,₅ = 180^.10^-6 Кл, так как конденсаторы С₄ и С₅ соединены последовательно.

6. Напряжение на 4 конденсаторе: U₄ = Q₄ / C₄ = 180^.10^-6 /12^.10^-6 = 15 В.

7. Напряжение на 3 конденсаторе: U₃ = U₄ + U₅ = 15 + 30 = 45 В.

8. Заряд конденсатора С₃: Q₃ = U₃ ^. C₃ = 45 ^. 8^.10^-6 = 360^.10^-6 Кл.

9. Общий заряд батареи и заряды конденсаторов С₁ и С₂:

Q = Q₁ = Q₂ = Q₃-₄ = Q₃ + Q₄,₅ = 360^.10^-6 + 180^.10^-6 = 540^.10^-6 Кл.

10. Напряжение на С₁ и С₂: U₁ = Q / C₁ = 540^.10^-6 / 24^.10^-6 = 22,5 В.

U₂ = Q / C₂ = 540^.10^-6 / 8^.10^-6 = 67,5 В.

11. Напряжение сети (напряжение последовательно соединенных конденсаторов С₁, С₂ и С₃-₄): U = U₁ + U₂ + U₃-₄ = 22,5 + 67,5 + 45 = 135 В.

12. Энергия электрического поля батареи конденсаторов:

W = C ^. U² / 2 = 4^.10 ^{-6 .}135² / 2 = 36,45^.10^-3 Дж.

В задачах № 13 -18 необходимо провести расчет простой электрической цепи

со смешанным соединением резисторов. Для их решения необходимо знать закон Ома

и первый закон Кирхгофа.

Рассмотрим решение примера.

Пример 3. На рис. 8 приведена схема соединения резисторов и источника энергии. Определить эквивалентное сопротивление цепи R_экв, ток в каждом резисторе, ЭДС

и мощность источника энергии P_ист , потенциал т. А, если известно, что R₁ = 7,5 Ом;

R₂ = 15 Ом; R₃ = 16 Ом; R₄ = 21 Ом; R₅ = 42 Ом; R₀ = 0,5 Ом; U₃ = 32 В.

I₃

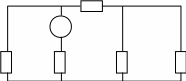
R₃

I₂ E, R₀ I₅ Рис. 8

I₄

R₂ I₁

R₁ R₄ R₅

Дано: R₁ = 7,5 Ом R₂ = 15 Ом R₃ = 16 Ом

R₄ = 21 Ом R5 = 42 Ом R₀ = 0,5 Ом U₃ = 32 В

Определить: R_экв, I₁, Е, Р_ист, φ_А

Решение.

1. Обозначим стрелками направление токов в каждом резисторе. Индексы токов

и напряжений на каждом резисторе принимаем соответствующими номеру резистора.

2. Эквивалентное сопротивление цепи R_экв определим путем постепенного упрощения –

«свертывания» схемы.

• R₄ и R₅ соединены параллельно, их общее сопротивление равно:

R₄,₅ = R₄^.R₅ / (R₄ + R₅) = 21^.42 / (21 + 42) = 14 Ом;

• R₃ и R₄,₅ соединены последовательно: R₃-₅ = R₃ + R₄,₅ = 16 +14 = 30 Ом;

• R₃-₅ и R₂ соединены параллельно:

R₂-₅ = R₂^.R₃-₅ / (R₂ + R₃-₅) = 15^.30 / (15 + 30) = 10 Ом;

• R₁ и R₂-₅ соединены последовательно: R_экв = R₁-₅ = R₁ + R₂-₅ = 7,5 + 10 = 17,5 Ом.

• По закону Ома для участка цепи определяем ток в резисторе R₃:

I₃ = U₃ / R₃ = 32 /16 = 2 А.

• I₄,₅ = I₃ = 2A, так как R₃ и R₄,₅ соединены последовательно.

• Определяем напряжение на сопротивлении R₄,₅: U₄,₅ = I₃^.R₄,₅ = 2^.14 = 28 B.

• По закону Ома токи в резисторах: I₄ = U₄,₅ / R₄ = 28 /21 = 1,33 A;

I₅ = U₄,₅ / R₅ = 28 /42 = 0,67 A;

• Напряжение на втором резисторе: U₂ = U₃-₅ = U₃ + U₄,₅ = 32 + 28 = 60 B.

• Ток в резисторе: I₂ = U₂ / R₂ = 60 / 15 = 4 A.

• По первому закону Кирхгофа находим ток источника: I₁ = I₂ + I₃ = 4 +2 = 6 A.

• ЭДС источника: E = I₁^. (R_экв + R₀) = 6^.(17,5 + 0,5) = 108 B.

• Мощность источника энергии: P_ист = E ^. I₁ =108 ^. 6 =648 Вт.

Задачи № 19 – 24 предусматривают расчет сложной электрической цепи. Сложные цепи имеют несколько источников ЭДС, которые расположены в разных ветвях, и резисторы. Расчет сложной цепи сводится к определению токов во всех ветвях по величине и направлению по заданным ЭДС и сопротивлениям резисторов.

Существует несколько методов расчета сложных цепей. Рассмотрим их применение.

Пример 5.

Определить токи во всех ветвях цепи, если ЭДС источников Е₁=180 В, Е₂=96 В, их внутренние сопротивления R₀₁=0,1 Ом, R₀₂=2 Ом; сопротивления резисторов: R₁=7,9 Ом, R₂=20 Ом, R₃=32 Ом, R₄=10 Ом.

Задачу решить методом узловых и контурных уравнений, составленных по законам Кирхгофа. Составить уравнение баланса мощности.

B C R₄ K

I₁ I₃ I₂ E₂

R₁ R₀₂ Рис. 9

R₃

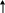I₁ I₃ I₂ R₂

D N

Метод узловых и контурных уравнений

Дано: E₁ = 180 B E₂ = 96 B R₁ = 7,9 Ом R ₃ = 20 Ом

R₀₁ = 0,1 Ом R₀₂ = 2 Ом R ₂ = 32 Ом R₄ = 10 Ом

Определить: I₁, I₂, I₃.

Решение.

Количество неизвестных токов равно количеству ветвей в цепи. На рис. 9 три ветви, следовательно, неизвестных токов три, для их нахождения необходимо составить систему

из трёх уравнений. Алгоритм расчета:

1. Обозначить контуры буквами.

2. На схеме произвольно показать предварительное направление токов (пунктир).

3. Составляем уравнения по первому закону Кирхгофа. Количество этих уравнений равно числу узлов в схеме без одного. На схеме два узла – С и Д, следовательно, составляем одно уравнение по первому закону Кирхгофа, например, для узловой точки С: I₁ + I₂ = I₃.

Остальные уравнения (3 – 1 = 2) составляются по второму закону Кирхгофа, т.е. два уравнения. Второе уравнение составим для контура АВСДА, направление обхода контура «по часовой стрелке»:

E₁ = I₁^. (R₁ + R₀₁) + I₃^.R₃.

Третье уравнение составим для контура СКNДС; направление обхода контура примем

«против часовой стрелки»:

E₂ = I₂^. (R₂ + R₀₂ + R₄) + I₃^.R₃.

4. Подставим исходные данные в полученную систему из трёх уравнений и решим систему относительно неизвестных токов:

I₁ + I₂ = I₃ I₁ + I₂ = I₃ (1)

E₁ = I₁^. (R₁ + R₀₁) + I₃^.R₃ 180 = I₁^. (7,9 + 0,1) + I₃ ^. 32 (2)

E₂ = I₂^. (R₁ + R₀₁ + R₄) + I₃^.R₃ 96 = I₂^. (20 +2 +10) + I₃ ^. 32 (3)

Из второго уравнения получим: 180 = 8^.I₁ + 32^.I₃, отсюда I₁=(180–32^.I₃)/8=22,5–4^.I₃ (а)

Из третьего уравнения получим: 96=32^.I₂+32^.I₃, отсюда I₂ = (96 – 32^. I₃)/32 = 3 – I₃ (б)

Подставим выражения (а) и (б) в первое уравнение и находим ток I₃:

22,5 – 4 ^. I₃ + 3 - I₃ = I₃; 22,5 + 3 = I₃ + 4 ^. I₃ + I₃; 25,5 = 6 ^. I₃; I₃ =25,5/6 = 4,25 A.

Значение тока I₃ подставим в выражения (а) и (б) и определяем токи I₁ и I₂:

I₁ = 22,5 – 4 ^. I₃ = 22,5 – 4 ^. 4,25 = 5,5 A; и I₂ = 3 – I₃ = 3 – 4,25 – 1,25 A.

Ток I₂ получился отрицательным, это значит, что первоначально принятое направление тока I₂ оказалось неверным и должно быть изменено на противоположное.

На схеме показываем действительное направление токов.

Пример 6. Определить токи во всех ветвях цепи по исходным данным примера 5 методом наложения.

Метод наложения

Решение.

1. Оставляем в схеме только источник с ЭДС Е₁; а источник с ЭДС Е₂ приравниваем к нулю, но его внутреннее сопротивление в схеме остается (рис. 10).

С R₄

•

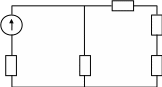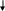E₁ R₀₂

I₁´ I₃´ I₂´

R₀₁

R₃

R₁ R₂

D Рис. 10

•

Рассчитывая получившуюся простую схему с одним источником и смешанным соединением резисторов, определяем частичные токи в ветвях, создаваемых в схеме источником Е₁ Показываем направление токов на схеме (рис. 10).

Определяем эквивалентное сопротивление схемы:

R´= R₁ + R₀₁ + = 7,9 + 0,1+ = 24 Oм

Ток в первой ветви: I´₁ = Е₁ / R´ = 180 / 24 = 7,5 А.

Напряжение между точками С и Д в схеме: U´_СД =E₁–I´₁^.(R₁+R₀₁)=180–7,5^.(7,9 =0,1)=120 B.

Токи во второй и в третьей ветвях: I´₂ = U´_СД / (R₂ + R₀₂ + R₄) = 120 / (20 + 2 + 10) = 3,75 A;

I´₃ = U´_СД / R₃ = 120 / 32 = 3,75 A.

2. Оставляем в схеме только источник Е₂, ЭДС Е₁ приравниваем к нулю, но его внутреннее сопротивление в схеме остаётся (рис.11).

C R₄

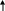
´´ I₂´´

Рис. 11

Рассчитывая получившуюся простую схему с одним источником и смешанным соединением резисторов, определяем токи ветвей, создаваемые источником Е₂.

Показываем направление токов на схеме. Рассчитываем эквивалентное сопротивление цепи: R´´ = R₂ + R₀₂ + R₄ + (R₁ + R₀₁) ^. R₃ / (R₁ + R₀₁ + R₃) =

= 20 + 2 + 10 + (7,9 +0,1) ^. 32 / (7,9 + 0,1 + 32) = 38,4 Ом.

Ток во второй ветви: I´´₂ = Е₂ / R´´ = 96 / 38,4 = 2,5 А.

Напряжение между точками С и Д в схеме:

U´´_СД = E₂ – I´´₂ ^. (R₂ + R₀₂ + R₄) = 96 – 2,5 ^. (20 + 2 + 10) = 16 B.

Токи первой и третьей ветвей: I´´₁ = U´´_СД / (R₁ + R₀₁) = 16 / (7,9 + 0,1) = 2 A;

I´´₂ = U´´_СД / R₃ = 16 / 32 = 0,5 A.

3. Для получения действительного тока в каждой ветви от действия двух ЭДС наложим друг на друга частичные токи, создаваемые каждым источником Е₁ и Е₂, путем алгебраического сложения, т.е. с учетом направления этих токов.

Если частичные токи ветви имеют одинаковое направление, то действительный ток равен их сумме и имеет то же направление.

Если частичные токи ветви имеют противоположные направления, то действительный ток определяется разностью (из большего по величине частичного тока вычитается меньший) и имеет направление большего тока.

Сравниваем частичные токи в первой ветви. Так как I₁´ и I₁´´ имеют противоположные направления и I₁´ > I₁´´ , то действительный ток в первой ветви: I₁= I₁´´- I₁´´ =7,5 - 2=5,5 A

и направление его совпадает с направлением тока I₁´, т.е. от т. Д к т. С. Определяем ток второй ветви: I₂´ > I₂´´ и имеют противоположные направления.

Ток второй ветви: I₂=I₂´- I₂´=3,75 - 2,5=1,25 A и его направление совпадает с направлением тока I´₂, т.е. от точки С к точке Д.

Частичные токи в третьей ветви имеют одинаковые направления, тогда ток в этой ветви определяется их суммой: I₃=I´₃+I₃´´=3,75+0,5=4,25 A и направление от точки С к точке Д.

Направление действительных токов показываем на исходной схеме.

Проверка по первому закону Кирхгофа: I₁ - I₂ - I₃= 0; 5,5 – 1,25 – 4,25 = 0.

Пример 7. Определить токи во всех ветвях по исходным данным примера 5 методом узлового напряжения.

Метод узлового напряжения.

Решение.

1. Предварительно направим токи ветвей к одному узлу – точке С (показываем пунктирными стрелками).

2. Рассчитываем проводимости ветвей: g₁ = 1/( R₁ + R₀₁)= 1/(7,9+0,1) = 1/8 = 0,125 См;

g₂ = 1/( R₂+ R₀₂ + R₄) = 1/(20+2+10) = 1/32 См; g₃ = 1/R₃ = 1/32 См.

3. Узловое напряжение:

U_{CD= =} (180·1/8 + 96·1/32) / (1/8 +1/32 +1/32) = (25,5 ·32)/6 =136В

4. Токи в ветвях: I₁ = (E₁ – U_CD) · g₁ = (180 – 136) · 1/8 = 5,5 A;

I₂ = (E₂ – U_CD) ·g₂ = (96 – 136) · 1/32 = - 1,25 A;

I₃ = (0 – U_CD) · g₃ = - 136 · 1/32 = - 4,25 A.

Направление тока I₁ совпадает с выбранным – от точки Д к точке С, т.к. знак тока «+».

Направление токов I₂ и I₃ противоположно выбранному ( знаки токов при расчетах «-»), т.е. токи I₂ и I₃ направлены от точки С к точке Д.

Показываем на заданной схеме действительное направление токов.

Расчет токов ветвей любым методом дает одинаковый результат, т.е. их величины и направление совпадают.

5. Составим уравнение баланса мощностей цепи.

В любой электрической цепи алгебраическая сумма мощностей источников энергии равна сумме мощностей, потребляемых сопротивлениями цепи (потребителей), и мощность потерь внутри источников, т.е. Р_ист = Р_потр + Р_о.

В левой части уравнения мощность источника, работающего в режиме генератора, учитывается со знаком «+», в режиме потребителя – со знаком «-«. Режим работы источника определяется по направлению действия ЭДС и положительному направлению тока данной ветви: если эти направления совпадают, то источник работает в режиме генератора; если не совпадают, то источник работает в режиме потребителя.

Для данной цепи: E₁ · I₁ – E₂ · I₂ = I₁² · (R₁ + R₀₁) + I₂² · ( R₂ + R₀₂ + R₄) + I₃² ·R₃;

180·5,5 – 96·1,25 = 5,5² · (7,9 + 0,1) + 1,25² · (20 + 2 + 10) + 4,25² · 32;

990 – 120 = 242 + 50 + 578; 870 Вт = 870 Вт.

В задачах 25 – 30 предусматривается выполнение расчета магнитной цепи.

Расчет неразветвленной магнитной цепи в большенстве случаев сводится к определению намагничивающей силы Iw, которая требуется для получения заданного магнитного потока Ф или магнитной индукции В. При этом указываются размеры и материал всех участков магнитной цепи.

Расчет магнитной цепи ведется по средней магнитной линии, по которой вся цепь делится на однородные участки, т.е. имеющие одинаковое сечение и один материал.

Пример 8. Магнитопровод электромагнитного реле содержит два участка: из ферромагнитного материала и воздушного зазора (рис. ). Размеры магнитопровода по средней магнитной линии: ℓ_ст = 60 см, ℓ_о = 0,157 мм. Сечение магнитопровода S = 2 см².

В стержне, на котором расположена обмотка, требуется создать магнитную индукцию

В = 0,8 Тл. Определить магнитный поток Ф в данной магнитной цепи. Найти ток I , который необходимо пропустить по обмотке, чтобы создать заданную магнитную индукцию В. Обмотка имеет w = 1000 витков.

Рассчитать силу F притяжения якоря электромагнитного реле и индуктивность L катушки.

Дано: В = 0,8 Тл, w = 1000, S = 2 см² = 2·10^-4 м²,

ℓ_cт = 60 мм = 60·10^-3 м, ℓ_о = 0,157 мм = 0,157 _*10^-3 м.

Определить: I, L, Ф, F.

Решение.

1. По заданной магнитной индукции определяем магнитный поток.

Ф = В·S = 0,82·10^-4 = 16·10^-5 Вб.

2. По кривой намагничивания определяем напряженность магнитного поля для участка из ферромагнитного материала:

при В = 0,8 Тл напряженность магнитного поля Н_ст = 20 А/см = 2000 А/м.

3. Напряженность магнитного поля в воздушном зазоре:

Н_о = В/(μ_а) = В/(μ ·μ_о) = 0,8/(1·4·π·10^-7) = 6,37·10⁵ А/м.

4. По закону полного тока определяем намагничивающую силу Iw:

Iw=H_ст·ℓ_ст+H_o·ℓ_o=2000·60·10^-3+6,37·10⁵·0,157·10^-3=120+100=220 A.

5. Находим ток в катушке реле: I = Iw/w = 220/1000 = 0,22 A.

6. Индуктивность катушки: L = wФ/ I = 1000·16·10^-5 / 0,22 = 0,73 А.

7. Сила притяжения якоря реле: F=B²·S/2 =0,82·2·10^-4/2·4 ·10^-7 = 51 H.

При увеличении воздушного зазора намагничивающая сила останется прежней, но основная его часть придется на воздушный зазор, т.е. закон полного тока принимает вид:

Iw = H_o·ℓ_o при H_ст ·ℓ_ст ~ 0.

Изменится напряженность магнитного поля в воздушном зазоре Н_о, значит, изменится магнитная индукция В= μ_а·Н_о и сила притяжения якоря электромагнитного реле.

В задачах 31 – 36 рассматривается явление электромагнитной индукции в прямолинейном проводнике, перемещающемся в однородном магнитном поле: принцип работы электрического генератора и двигателя. Для успешного решения этих задач следует изучить тему «Электромагнитная индукция» учебного пособия Частоедова.

Пример 9. В однородном магнитном поле с индукцией В=0,8 Тл по параллельным направляющим без трения передвигаются два проводника перпендикулярно к направлению силовых линий магнитного поля, которое показано на рис 12.

a c

ℓ υ₂ υ₁ Рис. 12

R₀₁ R₀₂

b d

Правый проводник движется под действием внешней силы влево равномерно со скоростью υ₁=15 м/с, другой – под действием электромагнитной силы со скоростью υ₂=12 м/с.

Длина проводников ℓ = 90 см, их сопротивление R₀₁= R₀₂=0,2 Ом, сопротивлением направляющих пренебречь.

Определить величину и направление тока в контуре, ЭДС и противо-ЭДС, внешней и электромагнитной сил.

На схеме показать направление тока, наведенных ЭДС и всех сил. Составить баланс мощностей.

I

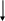
а c

+ F_эм E_пр + + + F Е F_торм

+ + +

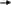
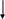
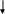+ + + + + + + + В

b R₀₁ d R_o2

1. По закону электромагнитной индукции в правом проводнике наводится ЭДС:

E₁=B·ℓ ·υ₁·sin α= 0,8·0,9·1 = 10,8 B, sin 90^o=1,

направление ЭДС определяется по правилу правой руки.

2. В замкнутом контуре abcd под действием ЭДС Е протекает ток (начальный, при не

подвижном проводнике): I_нач = E / (R₀₁+R₀₂) = 10,8 / (0,2+0,2) = 27 A.

Направление тока совпадает с направлением действия ЭДС Е₁.

3. На проводники с током в магнитном поле действует электромагнитная сила (начальная): F_эм._нач= B·I_нач·ℓ ·sin α= 0,8·27·0,9·1 = 19,44 H

Направление этой силы определяется по правилу левой руки.

4. Проводник ab под действием силы F_эм начнет передвигаться влево, а по закону

электромагнитной индукции наводится ЭДС:

E₂=B·ℓ·υ₂·sin α = 0,8·0,9·12·1 = 8,64 B.

Направление ЭДС определяется по правилу правой руки.

5. В замкнутом контуре действует две ЭДС Е₁ и Е₂, направленные встречно друг другу, тогда ток в движущихся проводниках определяем по закону Ома:

I = (E₁ – E₂) / (R₀₁+R₀₂) = (10,8 - 8,64) / (0,2+0,2) = 5,4 A.

Направление тока совпадает с действием большей ЭДС, проводник работает в режиме генератора. ЭДС Е₂ направлена против тока в проводнике и поэтому она называется противо-ЭДС: E_пр = E₂ = 8,64 B

6. Электромагнитная сила, действующая на движущиеся проводники с током I = 5,4 А.

F_эм = B·I·ℓ·sin α= 0,8·5,4·0,9·1 = 3,888 H.

Направление этой силы на каждый проводник определяется по правилу левой руки.

Сила F_эм , действующая на проводник cd, направлена против движения проводника, носит тормозной характер, т.е. , F_эм = F_торм. При равномерном движении проводника должно сохраняться равенство внешней силы и тормозной: F = F_торм = 3,888 Н.

Направление перемещения проводника ab совпадает с направлением силы F_эм, действующей на проводник ab, т.е. сила является движущей.

Проводник ab работает в режиме двигателя.

7. Механическая мощность внешней силы, действующая на проводник cd:

P_мех1 = F·υ₁ = 3,888·115 = 58,32 Вт.

Эта мощность преобразуется в электрическую в проводнике cd:

P_эл1 = E₁ · ℓ = 10,8 · 5,4 = 58,32 Вт.

Мощность Р_эл1 частично преобразуется в тепловую в проводнике cd:

P_тепл1 = I² · R₀₁ = 5,4² · 0,2 = 5,832 Вт,

остальная часть электрической мощности передается проводнику ab:

Р_эл2 = Р_эл1 – Р_тепл1 = 58,32 – 5,832 = 52,488 Вт,

В проводнике ab электрическая мощность Р_эл2 расходуется на механическое движение и покрытие тепловых потерь:

P_мех2 = F_эм · υ₂ = 3,888 ·12 = 46,656 Вт; P_тепл2 = I² · R₀₂ = 5,4² · 0,2 = 5,832 Вт.

Баланс мощности для проводника cd (генератор): Р_мех1 = Р_эл1 = Р_тепл1 + Р_эл2.

Баланс мощности для проводника ab (двигатель): Р_эл2 = Р_тепл2 + Р_мех2.

Баланс мощности для всей установки: Р_мех1 = Р_эл1 = Р_тепл1 + Р_тепл2 + Р_мех2

58,32 = 58,32 = 5,832 + 5,832 + 46,656; 58,32 Вт = 58,32 Вт = 58,32 Вт.