
- •Содержание
- •Пояснительная записка
- •Перечень практических заданий
- •Практическое занятие №1
- •Практическое занятие №2
- •Г еометрический смысл производной. Если кривая задана уравнением , то — угловой коэффициент касательной к графику функции в этой точке ( ).
- •Практическое занятие №3
- •Практическое занятие №4
- •Практическое занятие №5
- •Практическое занятие №6
- •Практическое занятие №7
- •Практическое занятие №8
- •Практическое занятие №9
- •Практическое занятие №10
- •Высшая математика для заочников и не только. - http://www.Mathprofi.Ru/index.Html
Практическое занятие №8
Тема: ВЫЧИСЛЕНИЕ ОБЪЕМОВ ДЕТАЛЕЙ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ В ФОРМЕ МНОГОГРАННИКОВ, ЦИЛИНДРА И КОНУСА
Цель работы: отработать навыки измерения основных элементов предложенной модели; умения вычислять площади поверхности и объёма данного геометрического тела.
Задачи: 1. Развивать коммуникативные компетенции (как способности работать с методическими рекомендациями);
2. Развивать предметные компетенции (объемы тел);
3.Формировать ключевые компетенции (информационная: систематизировать, анализировать, использовать и обрабатывать полученную информацию).
Оборудование: методические рекомендации, письменные принадлежности.
Теоретическое обоснование:
Указания по выполнению практического занятия:
Решить задачи на нахождение объема:
Задача 1. Образующая прямого конуса равна 4 см и наклонена к плоскости основания под углом 300. Найдите объём конуса.
Задача 2. Железобетонная панель имеет размеры 600 х 120 х 22 см. По всей её длине 6 цилиндрических отверстий, диаметр которых 14 см. Найдите массу панели, если плотность материала 2,5 т/м3.
Задача 3. Металлический шар радиусом 100мм надо перелить в цилиндр, высота которого равна 100мм. Найдите длину радиуса основания цилиндра.
Задача 4. Стаканчик для мороженного конической формы имеет 12см глубину и 5см по диаметру верхней части. На него сверху положили две ложки мороженного в виде полушарий диаметра 5см. Переполнит ли мороженное стаканчик если позволить ему растаять.
Задача 5. Инженер, рост которого 180см пришел рассмотреть новую сферическую цистерну для хранения воды. Он забрался в пустую цистерну, и, когда он поднялся на место, находящееся в 5м 40см над точкой, в которой цистерна упирается на землю, его голова коснулась верхнего края цистерны. Зная, что город потребляет в час 40тысяч литров воды, он немедленно рассчитал, на сколько часов может хватить полной цистерны. Как он это сделал и как он получил результат.
Задача 6. На полке в магазине стоят две банки земляничного варенья одного и того же сорта. Одна банка в 2 раза выше другой, но зато её диаметр в 2 раза меньше. Высокая банка стоит 23 цента, а низкая 43 цента. Какую купить выгоднее?
Задача 7. Основание прямого кругового конуса имеет диаметр 12 см, а высота конуса равна 12см. Конус наполнили водой, затем в конус опустили шар так, что он оперся на стенки конуса. Над водой при этом оказалось ровно половина шара. Сколько воды осталось в конусе после того, как шар был вынут?
Задача 8. Яма в форме правильной усеченной четырехугольной пирамиды имеет объем 133 м3. Найдите ее глубину, если сторона верхнего основания 9 м, а нижнего - 4м
Задача 9. Куча щебня по краям шоссейной дороги представляет собой конус. Окружность основания конической кучи щебня 12,1 м. Длина образующей 4,6 м. Каков объем кучи?
Задача 10. Какое количество кирпича сможет перевезти машина, имеющая размеры кузова 3,6м*2,3м*1м? Размеры кирпича 25см*12см*8см.
Практическое занятие №9
Тема: ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И СВЯЗАННЫХ С НИМИ РАСЧЕТОВ
Цель работы: систематизация навыков и умений, обучающихся по применению знаний, полученных в ходе изучения темы «Производная и ее применение»
Задачи: 1. Развивать коммуникативные компетенции (как способности работать с методическими рекомендациями);
2. Развивать предметные компетенции (вычисление производной,);
3.Формировать ключевые компетенции (информационная: систематизировать, анализировать, использовать и обрабатывать полученную информацию).
Оборудование: методические рекомендации, письменные принадлежности.
Теоретическое обоснование:
В чём заключается механический смысл производной?
Ответ. Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке.
2. Если функция задана законом прямолинейного движения S = S(t), то S'(t)?
Ответ. Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t)
Что есть вторая производная от закона движения?
Ответ. Скорость изменения скорости этого движения, то есть ускорение а(t) = v' (t) = S' ' (t).
С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х.
Выясняем формулы из физики, где используется производная.
υ(t) = х'(t) – скорость.
a(t) = υ'(t) – ускорение.
I(t) = q'(t) – сила тока.
с(t) = Q'(t) – теплоемкость.
d(l) = m'(l) – линейная плотность.
K(t) = l'(t) – коэффициент линейного расширения.
ω(t) = φ'(t) – угловая скорость.
e(t) = ω'(t) – угловое ускорение.
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности.
N(t) = A'(t) – мощность.
F(x)= A'(x) – Сила есть производная работы по перемещению.
Е = Ф'(t) – ЭДС индукции F = р'(t) – 2 закон Ньютона.
Примеры применения производной в физике |
|
Задача |
Решение |
Тело массой 4 кг движется прямолинейно по закону x(t)=t2+t+1.
|
x ' (t) = v (t) = 2t+1, v (3) = 7, a(t)= v' (t) = 2, Wк = (4·72)/2=98 2. F = ma, a(t) = v' (t) = x' ' (t), x ' (t) = v (t) = 2t+1, a(t)= v' (t) = 2, F = ma = 4·2 = 8 H.
|
Угол поворота тела вокруг оси изменяется по закону φ(t)=0,1t2-0,5t+0,2.
Найти угловую скорость вращения тела в момент времени t=20с. |
ω(t) = φ'(t) φ'(t) = 0,2t-0,5 ω(t) = 0,2t-0,5 ω(20) = 3,5 |
Для любой точки С стержня АВ длиной 10 см, масса куска стержня АС определяется по формуле m(l)=3l2+5l.
Найти линейную плотность стержня в середине отрезка АВ, в конце отрезка. |
d(l) = m'(l) m'(l) = 6l+5 d(l) = 6l+5 d(5) = 6·5+5=35 – в середине отрезка d(10) = 6·10+5=65 – в конце отрезка |
Количество электричества, протекающее через проводник, начиная с момента времени t=0, задаётся формулой q=3t2-3t+4.
Найти силу тока в конце 6-й секунды. |
I(t) = q'(t) q'(t) = 6t-3 I(t) = 6t-3 I(6) = 6·6-3=33 |
Алгоритм решения задач на нахождение оптимального решения:
- определить исследуемую функцию;
- ввести переменную;
- установить область определения функции;
- вычислить max/min функции на заданном интервале.
ЗАДАЧА 1: Дан прямоугольный лист жести (АВ = 80см, ВС = 50см). Надо вырезать около всех углов одинаковые квадраты так, чтобы после загибания оставшихся кромок получилась открытая сверху коробка максимальной вместимости.
РЕШЕНИЕ:
 V(x)
= ( 80-2x)( 50-2x)x V(x)
= 4x3
– 260x2
– 4000x
V(x)
= ( 80-2x)( 50-2x)x V(x)
= 4x3
– 260x2
– 4000x
D(V) = (0;25), т.к. V(x) > 0
( 80-2x)( 50-2x)x > 0
x1 = 40, x2 = 25, x3 = 0

0 < x < 25
V′ (x) = 12x2 – 520x + 4000
V′ (x) = 0, 12x2 – 520x + 4000 = 0
3x2 – 130x + 1000 = 0
D = 4900
x1
= 10, x2
=
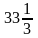
x1 Є (0;25)

Vmax (x) = V(10) = 1800см3
Ответ: Объем коробки будет максимальным, если сторона вырезаемого квадрата равна 10см.
ЗАДАЧА
2: Пусть электрическая лампочка движется
с помощью блока вдоль вертикальной
прямой ОВ. На каком
расстоянии от горизонтальной плоскости
следует ее разместить, чтобы в точке А
этой плоскости освещённость была
наибольшей (ОА = а, ∟ОАВ =
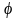 ,
ВА = r)?
,
ВА = r)?
РЕШЕНИЕ:

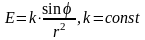
Пусть
ВО = х, тогда
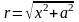 ,
,
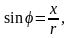 где 0 < х < + ∞
где 0 < х < + ∞
Значит,
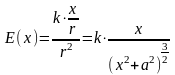
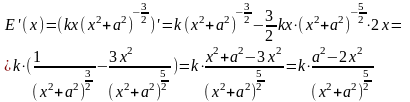
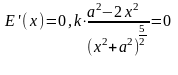
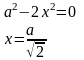
Т.к. функция Е(х) имеет одну критическую точку, а в условии сказано, что существует положение лампочки, при котором освещенность в точке А наибольшая, то х является искомой точкой.
Ответ:
для достижения наибольшей освещенности
лампочка должна висеть на высоте
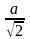 .
.
ЗАДАЧА 3: Вписать в данный шар радиуса R цилиндр с наибольшей боковой поверхностью.
РЕШЕНИЕ:
І способ - геометрический
способ - геометрический
Sб
= 2π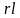 , т.к.
, т.к.
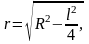 то Sб
= 2π
то Sб
= 2π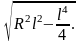
Рассмотрим и преобразуем выражение :
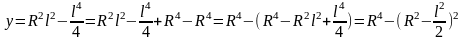
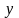 наибольшее=R4,
когда
наибольшее=R4,
когда

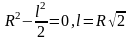
Тогда
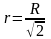 ,
а значит Sб
=
2π
,
а значит Sб
=
2π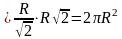 .
.
Ответ:
наибольшее значение Sб
=
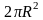 ,
при
,
при
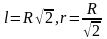 .
.
ІІ способ - алгебраический
 Sб
= 2π
Sб
= 2π
Т.К. это Sб = 2π
Обозначим
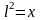 ,
тогда Sб
= 2π
,
тогда Sб
= 2π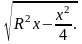
Рассмотрим
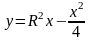 ,
0< х < 4
,
0< х < 4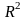
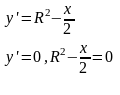 ,
,
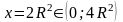
 max
=
max
=
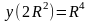 ,
т.о. Sб
max
= Sб
(
,
т.о. Sб
max
= Sб
(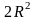 ) =
.
) =
.
Ответ: искомый цилиндр имеет Sб = .
Указания по выполнению практического занятия:
Задача 1 . Вписать в данный конус, радиус основания которого R и высота Н, цилиндр, имеющий наибольшую площадь полной поверхности.
Задача 2. Из круглого бревна диаметром 50см требуется вырезать балку прямоугольного сечения набольшей площади. Какие должны быть размеры сторон поперечного сечения балки?
Задача 3. Тело массой 2 кг движется прямолинейно по закону x(t)=t2+t+1. Найти действующую на тело силу F, кинетическую энергию тела через 2с после начала движения.
Задача 4. Маховик, задерживаемый тормозом, за время t поворачивается на угол φ(t)=4t-0,3t2. Найти угловую скорость ω(t) вращения маховика в момент времени 2 с.
Задача 5. Найти скорость тела, движущегося по закону s(t)=3t+5.
Задача 6. Тело движется прямолинейно по закону s(t)=2t2-t+4. Найти скорость тела в моменты времени t1=0, t2=2, t3=5 с.
Задача 7. Тело движется прямолинейно по закону s(t)=1-2t+t3. Найти скорость и ускорение в момент времени t=3с.
Задача 8. Когда скорость точки, движущейся прямолинейно по закону s(t)=t2-4t+5, равна 0?
Задача 9. Количество теплоты Q, получаемое некоторым веществом при нагревании определяется по формуле Q=10t+0,5t2. Найти теплоёмкость этого вещества при 20 К.
Задача 10. Закон изменения температуры Т тела в зависимости от времени задан уравнением T=0,3t2. С какой скоростью нагревается это тело в момент времени 10 с.
Задача 11. Температура тела изменяется по закону T(t)=0,5t2-2t. С какой скоростью нагревается тело в момент времени t=6с.
