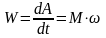- •Энергия материальной системы Работа силы
- •Потенциальная энергия
- •Кинетическая энергия
- •Кинетическая энергия твердого тела.
- •Закон сохранения энергии
- •Принцип Даламбера для материальной системы
- •Силы инерции твердого тела
- •Общие теоремы динамики для материальной точки, системы и твердого тела Количество движения
- •Элементарный и полный импульс силы
- •Теорема об изменении количества движения Теорема об изменении количества движения точки
- •Теорема об изменении количества движения механической системы
- •Законы сохранения количества движения
- •Момент количества движения (кинетический момент)
- •Момент количества движения твердого тела относительно оси вращения при вращательном движении твердого тела
- •Теорема об изменении момента количества движения точки
- •Теорема об изменении момента количества движения системы
- •Теорема об изменении момента количества движения системы относительно центра масс
- •Законы сохранения момента количества движения
- •Теорема об изменении кинетической энергии точки.
- •Теорема об изменении кинетической энергии системы.
Энергия материальной системы Работа силы
Р абота
- одна из основных характеристик силы,
оценивающих действие силы на тело при
некотором его перемещении. Если точка
приложения силы движется по прямолинейной
траектории, то работой постоянной по
величине и направлению силы
абота
- одна из основных характеристик силы,
оценивающих действие силы на тело при
некотором его перемещении. Если точка
приложения силы движется по прямолинейной
траектории, то работой постоянной по
величине и направлению силы
 на перемещении s
называется выражение
на перемещении s
называется выражение

Работу будем считать положительной, если направление силы совпадает с направлением перемещения точки приложения силы из начального положения в конечное.
П оскольку
от выбора угла α или β зависит знак
работы, то удобнее брать всегда острый
угол α между вектором силы и траекторией.
Тогда, если вектор силы перпендикулярен
траектории, работа силы равна нулю.
оскольку
от выбора угла α или β зависит знак
работы, то удобнее брать всегда острый
угол α между вектором силы и траекторией.
Тогда, если вектор силы перпендикулярен
траектории, работа силы равна нулю.
Если вектор силы изменяется и точка приложения ее движется по кривой линии, то формула неприменима. В этом случае надо сначала вычислить элементарную работу силы на перемещении ds
Элементарная работа силы - скалярная величина, равная произведению элементарного перемещения на проекцию силы на это перемещение.
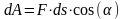 или
или
 .
,
.
,

Единицей
измерения работы в СИ является –

При
 при
при

Частные случаи: 


Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.

Если
сила
 задана своими проекциями (
задана своими проекциями (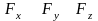 )
на оси координат и элементарное
перемещение задано своими проекциями
(
)
на оси координат и элементарное
перемещение задано своими проекциями
(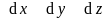 )
на оси координат, то элементарная работа
силы равна:
)
на оси координат, то элементарная работа
силы равна:
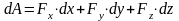 (аналитическое выражение элементарной
работы).
(аналитическое выражение элементарной
работы).
Работа силы на любом конечном перемещении
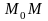 равна взятому вдоль этого перемещения
интегралу от элементарной работы.
равна взятому вдоль этого перемещения
интегралу от элементарной работы.
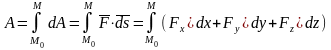
Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.
 ,
, 
Мощность равна скалярному произведению силы на скорость.
Единицей
измерения мощности в СИ является –

В технике за единицу силы принимается
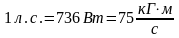 .
.
Работа веса тела (силы тяжести).
 Пусть тело перемещается вблизи
поверхности Земли из одного положения
в другое так, что центр тяжести его
движется по кривой линии.
Пусть тело перемещается вблизи
поверхности Земли из одного положения
в другое так, что центр тяжести его
движется по кривой линии.
Элементарная работа силы
 ,
постоянной и направленной вертикаль-но
вниз,
,
постоянной и направленной вертикаль-но
вниз,
dA = –Pdz . проинтегрировав выражение, получим
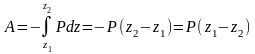
A = Ph
Следовательно работа веса тела (постоянной силы тяжести) не зависит от траектории движения центра тяжести. Определяется лишь высотой, на которую опустится или поднимется центр тяжести. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Работа силы упругости.
 Рассмотрим
материальную точку закрепленную на
упругом элементе жесткости с, которая
совершает колебания вдоль оси х. Сила
упругости (или восстанавливающая сила)
Рассмотрим
материальную точку закрепленную на
упругом элементе жесткости с, которая
совершает колебания вдоль оси х. Сила
упругости (или восстанавливающая сила)
 .
Пусть точка М, на которую действует
только сила упругости, перемещается из
положения
.
Пусть точка М, на которую действует
только сила упругости, перемещается из
положения
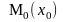 в положение
в положение
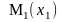 .
(
.
( ,
,
 ).
).
dA = –F∙dx = –cx∙dx
и тогда при перемещении конца пружины от положения х0 до х1 работа
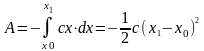 .
.
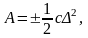
где – изменение величины деформации. Знак (–) ставится при увеличении деформации, (+) – при уменьшении.
Работа силы, приложенной к телу, вращающемуся вокруг неподвижной оси.
 точка приложения силы
движется по окружности радиуса r.
Элементарная работа
точка приложения силы
движется по окружности радиуса r.
Элементарная работа
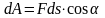 ,
где
,
где
 .
.
Поэтому
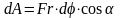 .
.
Но
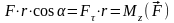 .
.
Значит,
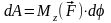
В
частности, если момент силы относительно
оси
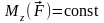 ,
работа силы при повороте тела на угол
φ равна
,
работа силы при повороте тела на угол
φ равна
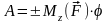 .
.
Знак работы определяется знаками момента силы и угла поворота. Если они одинаковы, работа положительная.
И з
формулы следует и правило определения
работы пары сил. Если пара с моментом m
расположена в плоскости перпендикулярной
оси вращения тела, то элементарная
работа пары сил равна
з
формулы следует и правило определения
работы пары сил. Если пара с моментом m
расположена в плоскости перпендикулярной
оси вращения тела, то элементарная
работа пары сил равна
 .
.
Полная
работа пары сил равна
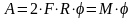
 -
угол поворота тела,
-
угол поворота тела,
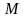 -
момент пары сил.
-
момент пары сил.
Мощность пары сил равна