Реакции связей

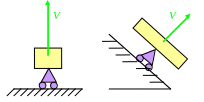
1. Идеальная (гладкая) поверхность или опора. Реакция перпендикулярна поверхности, нормальная реакция поверхности.

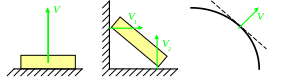
2. Идеальная нить. Реакция вдоль нити, троса.

3. Идеальный стержень. Реакция вдоль стержня.

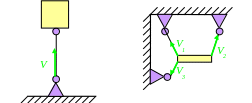
4. Шарнирно-подвижная опора – опора на катках. Реакция перпендикулярна поверхности.

5. Шарнирно - недвижимая опора. Реакция состоит из составляющих проекций на координатные оси.

6. Недвижимое закрепление – жесткая заделка. Осевые реакции и реактивный момент M.

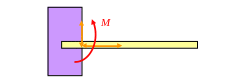
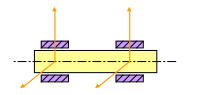
7. Цилиндрический шарнир или подшипник. Реакция из составляющих вдоль осей, перпендикулярных оси цилиндра.

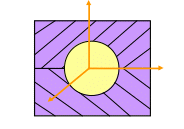
8. Сферический подшипник. Реакция из составляющих вдоль пространственных осей координат.

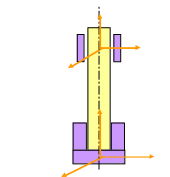
9. Упорный подшипник. Реакция из составляющих вдоль осей.

Основные гипотезы и принципы

1. Гипотеза о сплошности материала: тело, сплошное и непрерывное до деформации, остается таким же и в процессе деформации.

2. Гипотеза об однородности и изотропности: в любой точке тела и в любом направлении физико-механические свойства материала считаются одинаковыми.

3. Гипотеза о малости деформаций: по сравнению с размерами тела деформации настолько малы, что не изменяют положения внешних сил, действующих на тело.

4. Гипотеза об идеальной упругости: в заданных малых пределах деформирования все тела идеально упругие, т.е. деформации полностью исчезают после прекращения нагрузок.

5. Гипотеза плоских сечений: плоское сечение до деформирования остается плоским и после деформации.

Закон Гука и гипотеза о малости деформаций дают возможность применять принцип суперпозиции (принцип независимости или сложения сил): деформации тела, вызванные действиями нескольких сил, равняются сумме деформаций, вызванных каждой силой.

Принцип Сен-Венана: статически эквивалентные системы сил, действующие на малую, по сравнению с общими размерами тела, его часть, при достаточном отдалении от этой части вызывают одинаковые деформации тела.

Принцип затвердения: тело, испытывающее деформирование, затвердело и к нему можно применять уравнения статики.

Аксиомы статики

Аксиомы отображают свойства сил, действующих на тело.

1. Аксиома инерции (закон Галилея).

Под действием взаимно уравновешенных сил материальная точка (тело) находится в состоянии покоя или движется равномерно и прямолинейно.

2. Аксиома равновесия двух сил.

Д ве силы, приложенные к твердому телу, будут уравновешенные только в случае, когда они равны по модулю и направлены вдоль одной прямой в противоположную сторону. Эта аксиома является условием равновесия тела под действием двух сил.

3. Аксиома добавления и отбрасывания уравновешенных сил.

Д ействие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить или изъять любую уравновешенную систему сил.

Следствие: Не изменяя состояние абсолютно твердого тела, силу можно переносить вдоль ее линии действия в любую точку, сохраняя неизменными ее модуль и направление. Т.е., сила, приложенная к абсолютно твердому телу, является скользящим вектором.

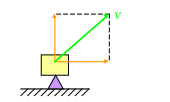
4. Аксиома параллелограмма сил.

Р авнодействующая двух сил, которые пересекаются в одной точке, приложена в точке их пересечения и определяется диагональю параллелограмма, построенного на этих силах как сторонах.

5. Аксиома действия и противодействия.

Каждому действию соответствует равное по модулю и противоположное по направлению противодействие.

6. Аксиома равновесия сил, приложенных к деформируемому телу при его затвердевании (принцип затвердевания).

Равновесие сил, приложенных к деформируемому телу (изменяемой системе), сохраняется, если тело считать затвердевшим (идеальным, неизменным).

7. Аксиома освобождения тела от связей.

Не изменяя состояния тела, любое несвободное тело, можно рассматривать как свободное, если отбросить связи, а их действие заменить реакциями.