Пример расчетов задач по теме «плоский поперечный изгиб балок»
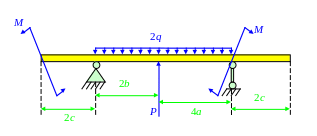
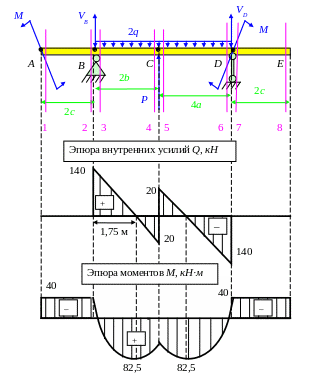
Задача 6. Балка № 5.
1. Для заданных 8 схем балок требуется построить эпюры Q и М с вычислением значений поперечных сил и изгибающих моментов в характерных сечениях балки.
2. Для схемы 5 подобрать номер указанного прокатного профиля, если [σ] = 160 МПа.
а = 0,5 м; b = 1 м; c = 0,5 м;
q = 40 кН/м; M = 40 кН·м; P = 30 кН;
[σ] = 160 МПа; I – двутавр.
1. Для заданной схемы балки построим эпюры Q и М с вычислением значений поперечных сил и изгибающих моментов в характерных сечениях балки.
а) Обозначим точки A, B, C, D, E. Отметим силы реакции опор VB и VD и определим их.
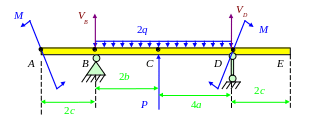
б) Сумма моментов сил относительно точки B равна нулю:
–2q · (2b + 4a) · (2b + 4a)/2 + P · 2b + M – M + VD · (4a + 2b) = 0,
VD = 140 кН.
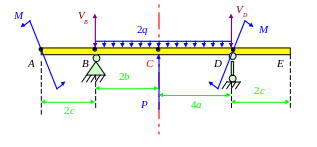
в) Сумма моментов сил относительно точки D равна нулю:
VB · (2b + 4a) + P · 4a – 2q(2b + 4a) · (2b + 4a)/2 = 0,
VB · (2 + 2) + 40 · 2 – 2 · 40 · (2 + 2) · (2 + 2)/2 = 0,
4VB = –80 + 40 · 16,
VB = –20 + 10 · 160,
VB = 140 кН.
Обратим внимание, что балка имеет ось симметрии, проходящую через точку C. Следовательно, VD = VB = 140 кН из условий симметрии. Можно было этим воспользоваться.
г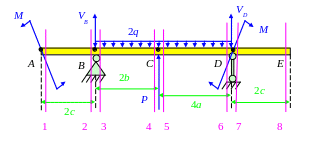
)
Построим эпюры Q
и М
методом сечений.
Q1 = Q2 = 0 кН;
Q3 = VB = 140 кН;
Q4 = VB – 2q · 2b = 140 – 80 · 2 140 – 160 = –20 кН;
Q5 = Q4 + P = –20 + 40 = 20 кН;
Q6 = Q5 – 2q · 4a = 20 – 80 · 20 = 20 – 160 = –140 кН;
Q7 = Q6 + VD = –140 + 140 = 0 кН.
Можно строить эпюру Q.
Найдем моменты в характерных поперечных сечениях:
M1 = –M = –40 кН·м;
M2 = M3 = M1 = –40 кН·м;
M4 = –M + VB · 2b – 2q · 2b · 2b/2 = –40 + 140 · 2 – 80 · 2 · 1 = 80 кН·м;
M5 = M4 = 80 кН·м;
M6 = –M + VB · (2b + 4a) – 2q · (2b + 4a) · (2b + 4a)/2 + P · 4a =
= –40 + 140 · 4 – 80 · 4 · 2 + 40 · 2 = –40 кН·м;
M7 = M8 = M6 = –40 кН·м.
На участке балки BD присутствует распределенная нагрузка, следовательно, поперечная сила меняется по линейному закону, а изгибающий момент – по закону квадратичной параболы, обращенной выпуклостью в сторону действия нагрузки, т.е. вниз. Найдем максимум изгибающего момента на участке BС. Для этого найдем координату x, в которой поперечная сила Q = 0.
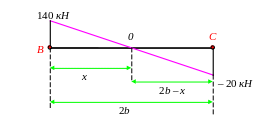
Из подобия треугольников:
x = 14 – 7x,
8x = 14,
x = 1,75 м.
Изгибающий момент найдем по площади под эпюрой Q. В данном случае находим площадь треугольника:
Mmax = 122,5 – 40 = +82,5 кН·м, на эпюре положительные значения моментов откладываем вниз.
Эпюра моментов должна быть симметрична, на участке балки CD также Mmax = 82,5 кН·м.
Можно строить эпюру M.
2. Подберем номер двутавра, если [σ] = 160 МПа.
Wz ≥ 5,156 · 10-4 м3 = 5,156 · 10-4 · 106 см3 = 515, 6 см3.
Из сортамента выбираем двутавр:
№ 33 (Wz = 597 см3);
№ 30 (Wz = 472 см3);
№ 30а (Wz = 518 см3).