Моменты сопротивления
1) Осевой момент сопротивления – это отношение осевого момента инерции относительно данной оси к расстоянию до точки поперечного сечения, наиболее удаленной от этой оси:
ymax и zmax – расстояния от главных осей Z и Y до точек, наиболее удаленных от них, Iz и Iy – главные центральные моменты инерции.
а
)
Прямоугольник.
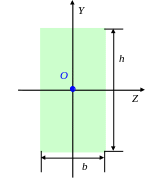
Аналогично,
б) Круг.
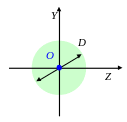
в) Кольцо.
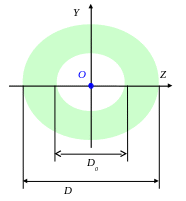
г) Для прокатных профилей моменты сопротивления приводятся в таблицах сортамента и в их определении нет необходимости.
2) Полярный момент сопротивления – это отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки поперечного сечения:
В качестве полюса обычно принимается центр тяжести сечения.
Д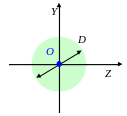
ля
круга:
Осевые моменты сопротивления Wz и Wy характеризуют чисто с геометрической стороны сопротивляемость стержня деформации изгиба, а полярный момент сопротивления Wρ – сопротивляемость кручению.
Пример расчетов задач по теме «геометрические характеристики плоских сечений»
Задача 4.
Для сечения, составленного из прокатных профилей, требуется:
1) вычертить сечение в масштабе на листах формата А4 и показать основные размеры;
2) определить положение центра тяжести и показать на чертеже положение горизонтальной и вертикальной центральных осей;
3) определить осевые и центробежный моменты инерции относительно центральных осей;
4) определить положение главных осей инерции и показать их на чертеже;
5) определить главные моменты инерции;
6) определить главные радиусы инерции.
1) вычертить сечение в масштабе на листах формата А4 и показать основные размеры.
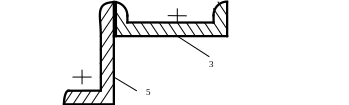
На схеме две цифры. Из таблицы на стр. 25 выписываем значения в столбцах только с этими номерами.
1, 2 |
|
Двутавры стальные горячекатаные
|
ГОСТ 8239-89
|
3, 4 |
|
Швеллеры стальные горячекатаные
|
ГОСТ 8340-97
|
9 |
|
Пластина
|
|
5, 6, 7, 8 |
|
Уголки стальные горячекатаные неравнополочные |
ГОСТ 8510-86 |
Данная схема состоит из уголка (5) и швеллера (3).
а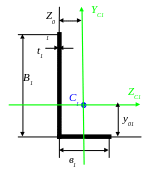
)
Уголок 180х110х10 мм3.
Из таблиц сортамента ГОСТ 8510-86 выписываем
исходные данные с индексами 1:
B1 = 90 мм = 9 см;
в1 = 56 мм = 5,6 см;
t1 = 8 мм = 0,8 см;
А1 = 11,18 см2;
Iz1 = 90,87 см4;
Iy1 = 27,08 см4;
z01 = 1,36 см;
y01 = 3,04 см;
Izy1 = 90,87 см4.
б) Швеллер №20. Из таблиц сортамента ГОСТ 8340-97 выписываем исходные данные с индексами 2:
h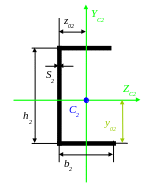
2
= 200 мм
= 20 см;
b2 = 76 мм = 7,6 см;
А2 = 23,4 см2;
S2 = 0,52 см;
Iz2 = 1520 см4;
Iy2 = 113 см4;
z02 = 2,07 см.
Из рисунка
в) Чертим сечение в масштабе на листах формата А4 и показываем основные размеры:
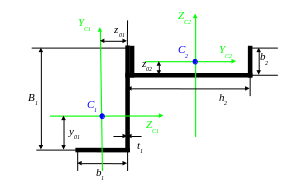
2) Определяем положение центра тяжести и показываем на чертеже положение горизонтальной и вертикальной центральных осей.
а) Выбираем оси и так, чтобы начало координат оказалось в левой нижней точке чертежа.
б) Найдем координаты центра уголка и швеллера.
Для уголка:
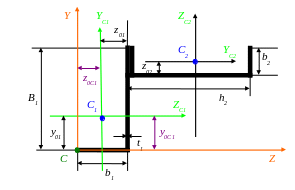
z0C1 = b1 – z01 = 5,6 – 1,36 = 4,24 см;
y0C1 = y01 = 3,04 см;
Для швеллера:
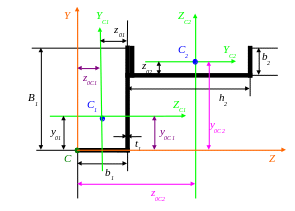
z0C2 = b1 + h2/2 = 5,6 + 20/2 = 15,6 см;
y0C2 = B1 – b2 + z02 = 9 – 7,6 + 2,07 = 3,47 см.
в) Координаты центра тяжести составного сечения (zc,yc):
Изобразим точку центра тяжести C(zC,yC) составного сечения и покажем положение горизонтальной ZC и вертикальной YC центральных осей на чертеже.
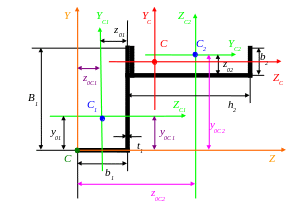
3) Определим осевые IzC и IyC моменты инерции относительно центральных осей YC и ZC, а также центробежный момент инерции IzуC.
Ось Z: IzC = IСz1 + IСz2
IСz1 – осевой момент инерции уголка относительно оси Z,
IСz2 – осевой момент инерции швеллера относительно оси Z.
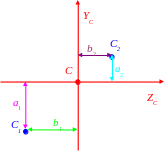
Для уголка:
IСz1 = Iz1 + a12 · А1.
Для швеллера:
IСz2 = Iz2 + a22 · А2.
Для составного сечения:
IzC = IСz1 + IСz2 =
= Iz1 + a12 · А1 + Iz2 + a22 · А2;
IzC = 90,87 + (3,04 – 3,331)2 · 11,18 +
+ 113 + (3,47 – 3.331)2 · 23,4;
IzC = 205,269 см4.
Аналогично, ось Y:
IСy1 – осевой момент инерции уголка относительно оси Y,
IСy2 – осевой момент инерции швеллера относительно оси Y.
IyC = IСy1 + IСy2 = Iy1 + (b1)2 · А1 + Iy2 + (b2)2 · А2;
IyC = 27,08 + (4,24 – 11,9272)2 · 11,18 + 1520 + (15,6 – 11,9272)2 · 23,4;
IyC = 2523, 394 см4.
Центробежный момент инерции составного сечения:
IzуC = IzC1yC1 + a1 ∙ b1 · А1 + IzC2yC2 + a2 · b2 · А2;
IzуC = 28,33 + (3,04 – 3,331)(4,24 – 11,9272) · 11,18 +
+ 0 + (3,47 – 3,331)(15,6 – 11,9272) · 23,4;
IzуC = 65,2855 см4.
4) Определим положение главных осей инерции. Для этого найдем угол φ0 наклона главных осей по отношению к центральным осям.
Покажем главные оси на чертеже:
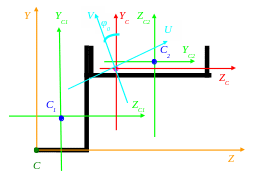
5) Найдем главные моменты инерции:
a
)
б) Iz(U) = IzC cos2φ0 + IyC sin2φ0 - IzCyC sin 2φ0 = 203,4316 см4,
Iy(V) = IyC cos2φ0 + IzC sin2φ0 + IzCyC sin 2φ0 =2525,231 см4.
6) Определим главные радиусы инерции.
