З адания для самостоятельного решения

1. Найти уравнение прямой:

а) образующей с осью Ох угол ^/₃ и пересекающей ось Оу в точке ( 0, - 6 );

б) параллельной оси Ох и отсекающей на оси Оу отрезок, равный 2;

с) отсекающей на осях координат, отрезки, равные 3 и 4.

Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых

Под углом между прямыми l₁ и l₂ плоскости

понимается наименьший (острый) из двух смежных

углов, образованных этими прямыми.

Если прямые заданы уравнениями с угловым коэф-

ф ициентом y = k₁x + b₁ и y = k₂x + b₂,

то угол φ между ними равен: tg φ = .

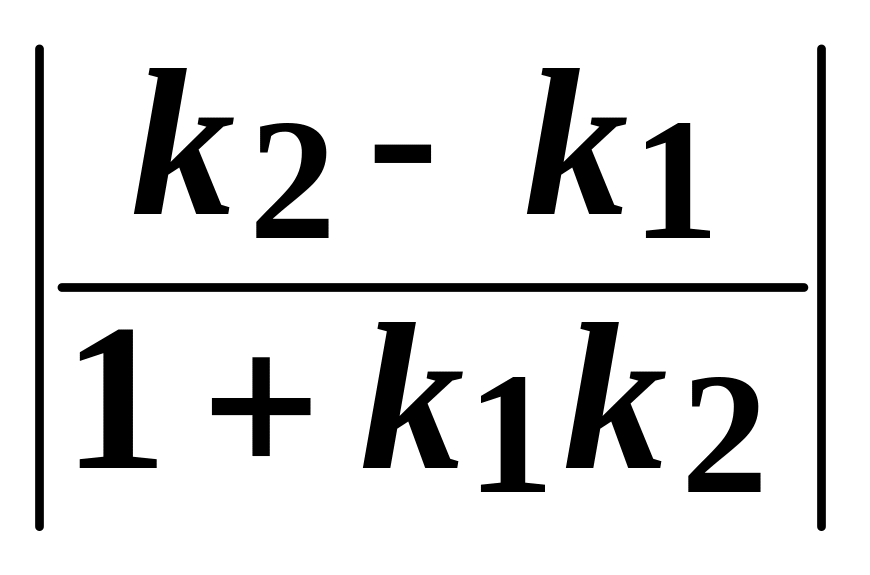Условие параллельности прямых l₁ и l₂: k₁ = k₂ .

Условие перпендикулярности прямых l₁ и l₂: k₁ = – (или k₁ k₂ = –1).

Если прямые l₁ и l₂ заданы общими уравнениями А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0,

то угол φ между ними равен углу между их нормальными векторами = {A₁; B₁} и

= {A₂; B₂}:

tg φ = .

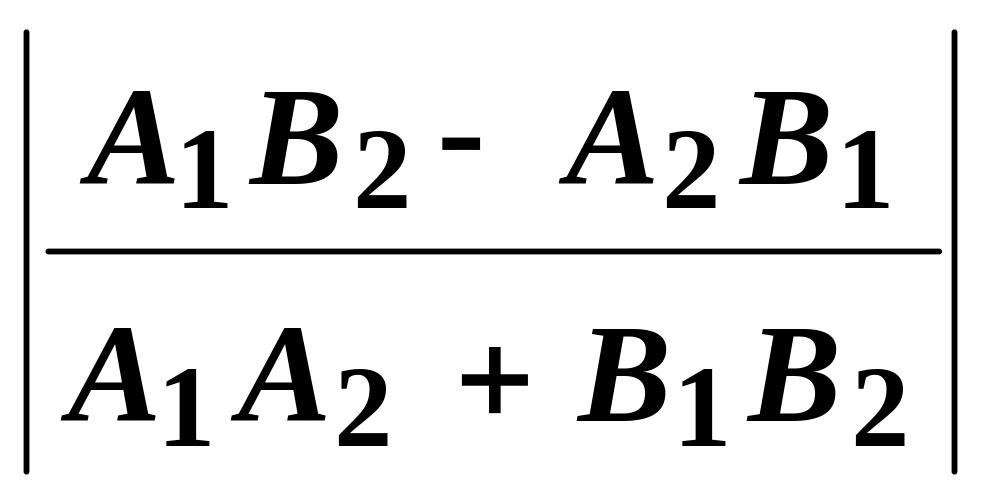Условие параллельности прямых l₁ и l₂: (или A₁ B₂ – А₂B₁ = 0).

Условие перпендикулярности прямых l₁ и l₂: A₁ А₂ + B₁B₂ = 0.

Для нахождения общих точек прямых l₁ и l₂ необходимо решить систему уравнений

или

При этом:

если , то имеется единственная точка пересечения прямых;

если , прямые не имеют общей точки, т.е. параллельны;

если , прямые совпадают.

Расстояние от данной точки до данной прямой

Расстоянием d от точки М₀ (x₀; у₀) до прямой Ах + Ву + С = 0 называется длина перпендикуляра, опущенного из этой точки на прямую:

d = .

Расстояние d от точки М₀ (x₀; у₀) до прямой х cos α + у sin α – p = 0:

d = | х₀ cos α + у₀ sin α – p |.

Пример 1. Найти угол между прямыми:

1) у = 2х – 3 и у = ^_ х + 5; 2) 2х – 3у + 10 = 0 и 5х – у + 4 = 0; 3) у = ³₄ х – 2 и 8х + 6у + 5 = 0.

1) Имеем: tg φ = = =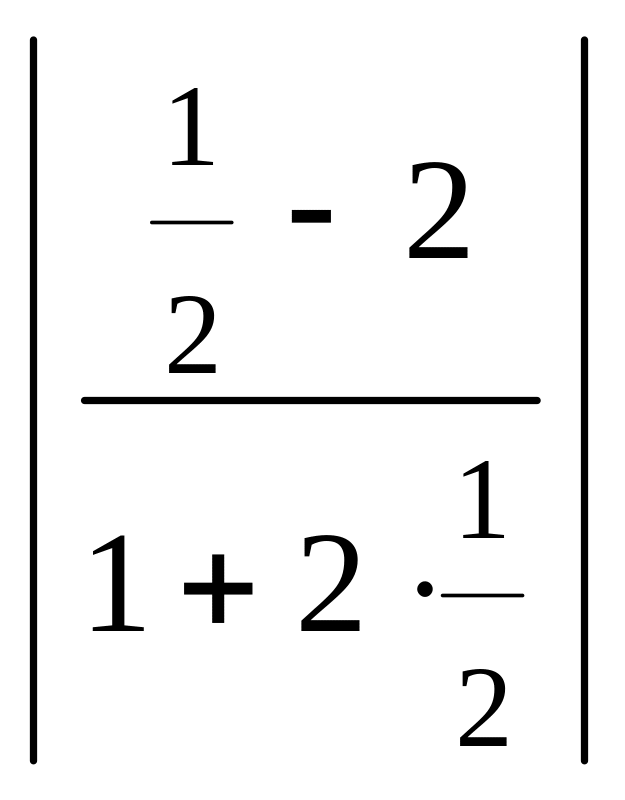 = , φ = arctg (φ ≈ 37º);

2) tg φ = = = = 1, φ = .

3) Здесь k₁ = , найдем k₂ . Для этого перейдем от 6у = –8х – 5 к эквивалентному равенству

у = – х – . Здесь k₂ = – . Т.к. k₁ · k₂ = –1, то данные прямые перпендикулярны.

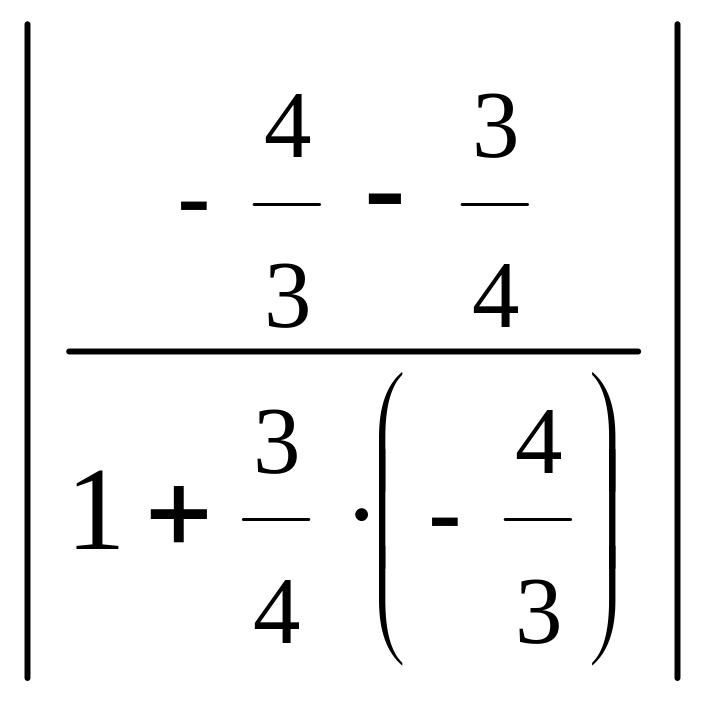Можно воспользоваться формулой: tg φ = = = ∞, φ = .

Задания для самостоятельного решения

1. Найти угол между прямыми: а) 3х + 2у – 1 = 0 и 5х – у + 4 = 0; б) у = 3,5х – 3 и 7х – 2у + 2 = 0;

в) х + 4у + 10 = 0 и 5у – 3 = 0.

2. Исследовать взаимное расположение следующих пар прямых:

а) 3х + 5у – 9 = 0 и 10х – 6у + 4 = 0; б) 2у = х – 1 и 4у – 2х + 2 = 0; в) х + у = 0 и х – у = 0;

г) 2х + 3у = 8 и х + у – 3 = 0.

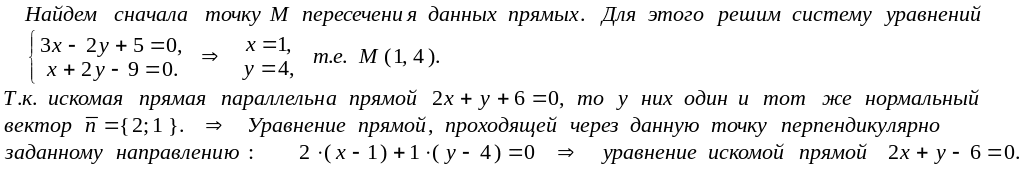Пример 2. Через точку пересечения 3х – 2у + 5 = 0, х + 2у – 9 = 0 проведена прямая, параллельная прямой 2х + у + 6 = 0. Составить ее уравнение.

Задания для самостоятельного решения

1. Найти уравнение прямой, проходящей через точку А ( -1, 2 ):

а) параллельно прямой у = 2х – 7; б) перпендикулярно прямой х + 3у - 2 = 0.

2. Найти уравнение прямой, проходящей через точку В ( 2, -3 ):

а) параллельно прямой, соединяющей точки М₁ ( - 4, 0 ) и М₂ ( 2, 2 );

б) перпендикулярно прямой х – у = 0.

Пример 3. Найти координаты точки М_2, симметричной точке М₁ ( - 3, 4 ) относительно

прямой 4х – у – 1 = 0.

Задания для самостоятельного решения

1. Точка А ( 2, -5 ) является вершиной квадрата, одна из сторон которого лежит на прямой

х – 2у – 7 = 0. Найти площадь этого квадрата.

2. Две стороны квадрата лежат на прямых 5х – 12у – 65 = 0 и 5х – 12у + 26 = 0. Найти площадь квадрата.

2. Найти уравнение прямой, проходящей через точку А ( 1, 2 ) так, чтобы расстояние от этой прямой до точек М₁ ( 2, 3 ) и М₂ ( 4, -5 ) были бы равны.

Пример 4. Написать уравнение прямой l ₂, проходящей через точку А ( 0, 2 ) под углом ^/₄ к

прямой l ₁: х – 2у + 3 = 0.

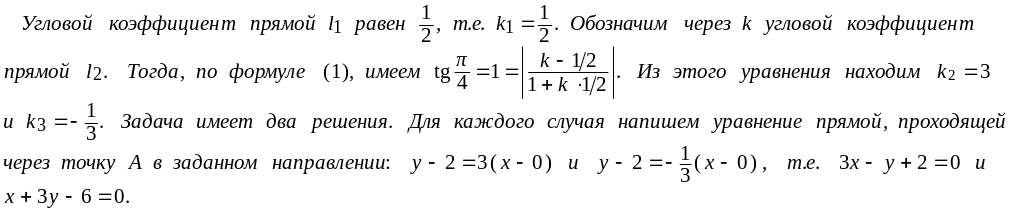
Смешанные задачи на прямую

Задания для самостоятельного решения

1. Найти площадь треугольника, образованного прямыми 2х + у + 4 = 0, х + 7у – 11 = 0 и

3х – 5у – 7 = 0 .

2. Составить уравнение прямой, проходящей через точку А ( - 2, 1 ):

а) параллельно оси Оу;

б) образующей с осью Ох угол ³/ ₄ ;

в) перпендикулярно вектору а = { 4; 2 };

г) параллельно биссектрисе первого координатного угла;

д) перпендикулярно прямой 6х – у + 2 = 0;

е) отсекающей на оси Оу отрезок длиной 5.

3. Дан четырехугольник ABCD с вершинами А ( 3, 5 ), B ( 6, 6 ), C ( 5, 3 ), D ( 1, 1 ). Найти:

а) координаты точки пересечения диагоналей;

б) угол между диагоналями.

3. Луч света, пройдя через точки А ( 4, 6 ) и B ( 5, 8 ), упал на прямую х – 2у + 2 = 0 и отразился от нее. Составить уравнение прямой, по которой направлен отраженный луч.

3. Известны вершины треугольника А ( -4, -2 ), B ( 0, 1 ), C ( 2, -1 ). Найти расстояние от начала координат до точки пересечения медианы, проведенной из вершины А, с высотой, проведенной из вершины В.

3. Найти координаты основания перпендикуляра, опущенного из точки А ( -1, 2 ) на прямую

3х – 5у – 21 = 0 .

7. Дан треугольник с вершинами в точках А ( 2, 5 ), B ( 5, -1 ), C ( 8, 3 ). Составить уравнение прямой, проходящей через точку пересечения медиан треугольника перпендикулярно к прямой х + у + 4 = 0.

8. Известны уравнения прямых, на которых лежат две стороны ромба: х + 2у – 4 = 0,

х + 2у – 10 = 0 и уравнение одной из его диагоналей х – у + 2 = 0. Найти координаты

вершин ромба.

9. Дан треугольник ABC с вершинами в точках А ( 2, 5 ), B ( 5, -1 ), C ( 8, 3 ). Найти координаты центра описанной около треугольника окружности.

10. Даны две вершины равносторонненго треугольника ABC : А ( -6, 0 ), B ( 0, 0 ). Найти

координаты третьей вершины С.

11. Даны вершины треугольника ABC : А ( 2, -2 ), B ( 3, 5 ), C ( 6, 1). Найти:

а) длины сторон АС и ВС;

б) уравнения прямых, на которых лежат стороны АС и ВС;

в) уравнение прямой, на которой лежит высота, проведенная из точки В;

г) длину этой высоты;

д) уравнение прямой, на которой лежит медиана, проведенная из точки А;

е) длину этой медианы;

ж) уравнение прямой, на которой лежит биссектриса угла С;

з) центр тяжести треугольника;

и) площадь треугольника;

к) угол С.