31

Аналитическая геометрия (семинары)

1. Прямоугольная система координат

Расстояние между двумя точками А(x₁, y₁) и В(x₂, y₂) на плоскости:

.

Расстояние между двумя точками А(x₁, y₁, z₁) и В(x₂, y₂, z₂) в пространстве:

.

Координаты (x, y) точки М, делящей в заданном отношении λ₁ : λ ₂ отрезок АВ, где А(x₁, y₁) и В(x₂, y₂) : .

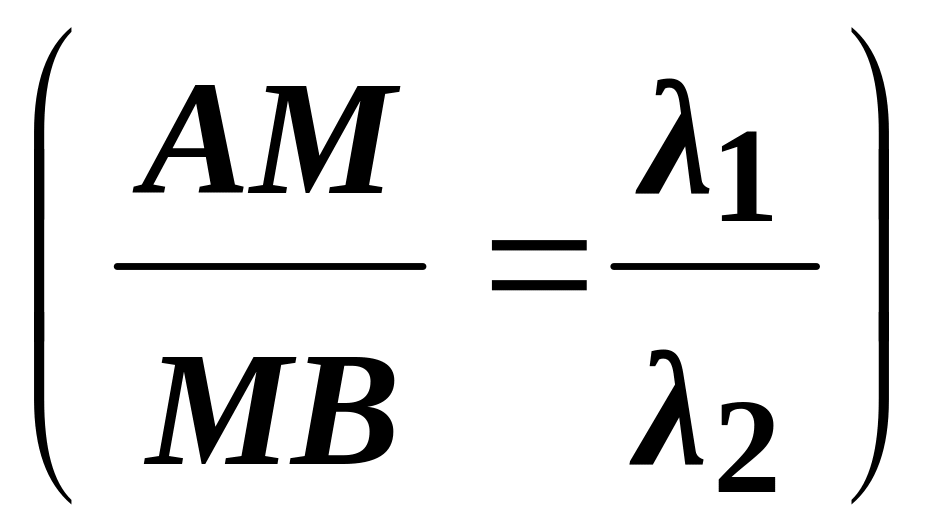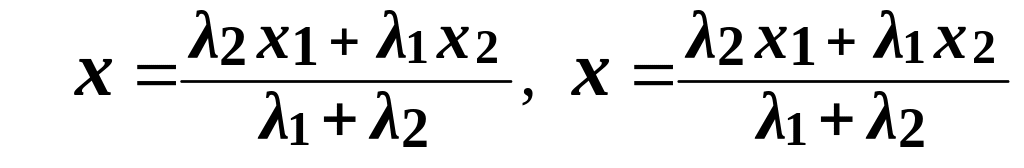Координаты (x, y) точки М, делящей в заданном отношении λ₁ : λ ₂ отрезок АВ, где А(x₁, y₁, z₁) и В(x₂, y₂, z₂) : .

В частности, при λ₁ = λ ₂ (точка М делит отрезок АВ пополам) :

.

2. Полярная система координат

П олярная система координат задается

точкой О, называемой полюсом, лучом Ор,

называемым полярной осью, и единичным

в ектором ē того же направления, что и луч Ор.

Положение точки М на плоскости определяется

д вумя числами: ее расстоянием r от полюса О и

углом φ, образованном отрезком ОМ с полярной осью

и отсчитываемым в положительном направлении.

Числа r и φ называются полярными координа-

тами точки М: r называют полярным радиусом,

φ – полярным углом (0 ≤ r ≤ +∞, 0 ≤ φ ≤ 2π).

Связь между полярными и прямоугольными координатами:

Определяя величину φ следует (по знакам х и у) определить четверть, в

которой лежит точка М, и учитывать, что -π < φ ≤ π.

2. Прямая на плоскости Различные виды уравнения прямой

Каждая прямая на плоскости Оху определяется линейным уравнением первой степени с

двумя неизвестными. Обратно, каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.

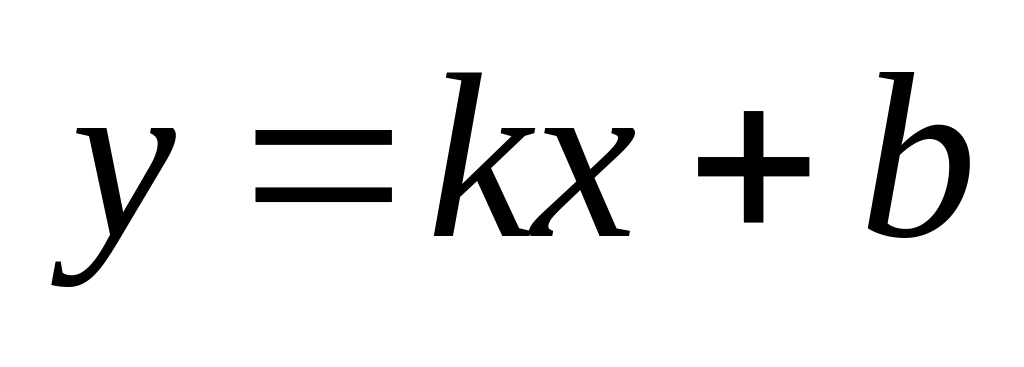1. У равнение прямой с угловым коэффициентом:

y = kx + b.

З десь: k – угловой коэффициент прямой (тангенс угла α,

который прямая образует с положительным направлением

оси Ох, k = tg α), b – ордината точки пересечения прямой с осью Оу.

2. О 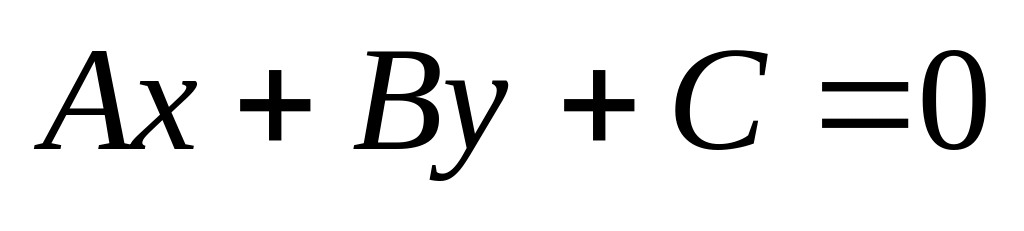бщее уравнение прямой:

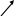
Ах + Ву + С = 0.

Вектор = {A; B} – нормальный вектор прямой (

п ерпендикулярен прямой).

Частные случая уравнения:

Ах + Ву = 0 (С = 0) – прямая проходит через начало координат;

Ах + С = 0 (В = 0) – прямая параллельна оси Оу;

Ву + С = 0 (А = 0) – прямая параллельна оси Ох;

А х = 0 (В = С = 0) – прямая совпадает с осью Оу;

В у = 0 (А = С = 0) – прямая совпадает с осью Ох.

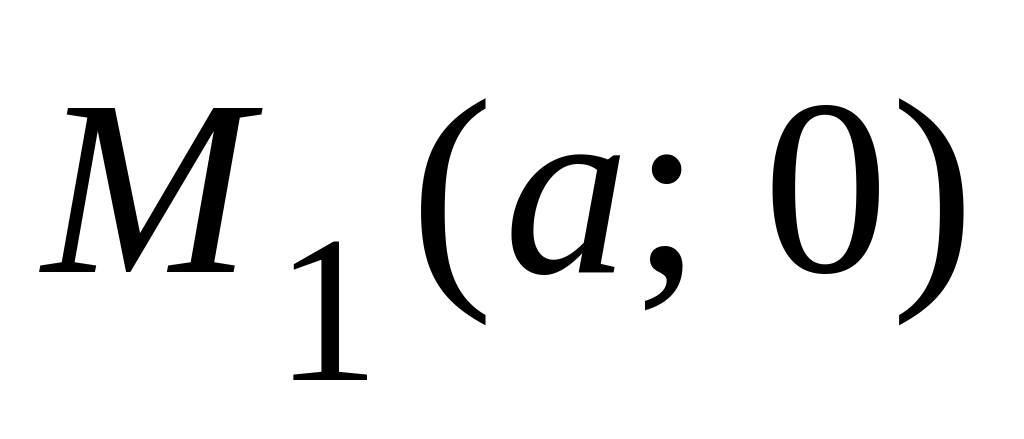3. У равнение прямой в отрезках: 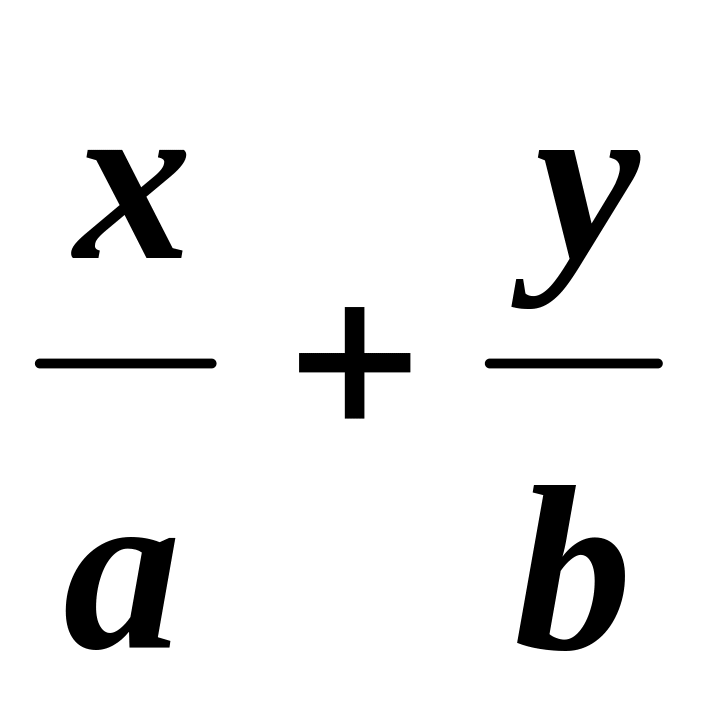= 1.

а и b – длины отрезков (с учетом знаков), отсекаемых прямой на осях Ох и Оу соответственно.

4. Уравнение прямой, проходящей через данную точку в данном направлении:

y – y₀ = k (x – x₀)

k = tg α (α – угол, образуемый прямой с осью Ох); (x₀; у₀) – координаты данной точки.

5. Уравнение y – y₀ = k (x – x₀) называют также уравнением пучка прямых с центром в точке (x₀; у₀).

Уравнение пучка прямых, проходящих через точку пересечения двух прямых А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0 имеет вид:

А₁х + В₁у + С₁ + λ ( А₂х + В₂у + С₂ ) = 0,

где λ – числовой множитель.