Государственный комитет российской федерации

ПО ВЫСШЕМУ ОБРАЗОВАНИЮ

Липецкий Государственный Технический Университет

Кафедра Электропривода

Лабораторная работа № 23

«ИЗМЕРЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЕМКОСТИ С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО ГАЛЬВАНОМЕТРА»

Выполнил студент 2 курса

гр. ЭП-99-1 ______________

_________________________

Преподаватель:

_________________________

Липецк 2000 г.

Цель работы: определение емкости испытуемых конденсаторов; изучение устройства и принципа действия баллистического гальва­нометра.

Приборы и принадлежности: баллистический гальванометр; источник тока (батарея элементов); вольтметр делитель напряже­ния, переключатели; эталонный конденсатор (известной емкости); испытуемые конденсаторы (неизвестной емкости); соединительные провода.

МЕТОДИКА ИССЛЕДОВАНИЯ

Определяемая в работе электрическая емкость характеризует способность проводника (или системы проводников) накапливать электрический заряд и энергию электрического поля. Из опыта из­вестно, что при изменении заряда проводника на величину q потенциал его изменяется пропорционально заряду на величину :

или (I)

Коэффициент пропорциональности С между зарядом и потенциалом называют электрической емкостью данного проводника (или системы проводников ).Электрическая емкость проводника зависит от его размеров, формы, свойств окружающей среда (диэлектрика) и расположения проводника относительно других проводников.

Формула (I) выражает физический смысл электрической емкости уединенного проводника: емкость численно равна количеству электри­чества, изменявшему потенциал проводника на единицу. За единицу измерения емкости в СИ принят фарад (Ф). Из формулы (I) следует, что

Так как фарад — слишком большая величина, для проводников, встречающихся на практике, используют дольные единицы емкости (микрофарад, мкФ , и пикофарад, пФ);

1 мкФ = 10^-6Ф ; 1 пФ = 10^-12 Ф

М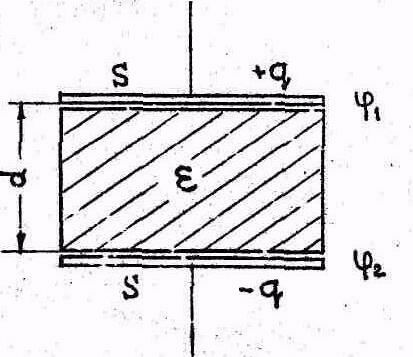ожно осуществить систему проводников, емкость которой практи­чески не зависит от окружающих тел, т.к. электрическое поле заря­женных проводников сосредоточено внутри системы. Примером таких систем являются конденсаторы - приборы, предназначенные для на­копления зарядов. В данной работе мы имеем дело с носкими кон­денсаторами, состоящими из двух или более плоских проводников (обкладок) и слоя диэлектрика между ними (рис.1).

В отличие от уединенного проводника, у которого при изменении заряда меняется потенциал относительно Земли ( _земли = 0), у конденсатора происходит изменение потенциала обкладок относительно друг друга, т.е. изменение разности потенциалов  = ₂ - ₁. Найдем коэффициент пропорциональности между разностью потенциалов  и зарядом на обкладках q , т.е. емкость конденсатора.

Разность потенциалов связана с напряженностью поля Е между обкладками:

 = E  d (2)

гдеd - расстояние между обкладками. Величина напряженности зависит от заряда на обкладках q

Здесь  - поверхностная плотность заряда;

 - диэлектрическая проницаемость среды между обкладками ;

₀ - электрическая постоянная;

S - площадь обкладок.

Подставляя (3) в (2), найдем связь заряда и потенциала для плоско­го конденсатора:

(4)

Сравнивая (4) с формулой (I), видим, что для плоского конденсатора электрическая емкость С равна

(5)

Если конденсатор заряжать от источника тока при напряжении U , то разность потенциалов пластин будет равна напряжению на конденсаторе:

₂ - ₁=  = U (6)

С учетом формул (4), (5) и (6) заряд на пластинах конденсатора при напряжении U равен

q = C  U (7)

Если напряжение на конденсаторе сделать больше определенного для данного конденсатора значения (напряжение "пробоя"), то между обкладками под действием сильного электрического поля возникает электрический разряд, создающий в диэлектрике проводящий канал. В результате конденсатор "пробивается", т.е. портится, и на его обкладках (из-за нарушения изоляции между ними) нельзя накапливать заряди. Поэтому каждый конденсатор характеризуется не только своей ёмкостью, но еще и максимальным рабочим напряжением.

Для того, чтобы в электрической цепи получить желаемую емкость при нужном рабочем напряжении, конденсаторы соединяют в батареи (рис.2).

П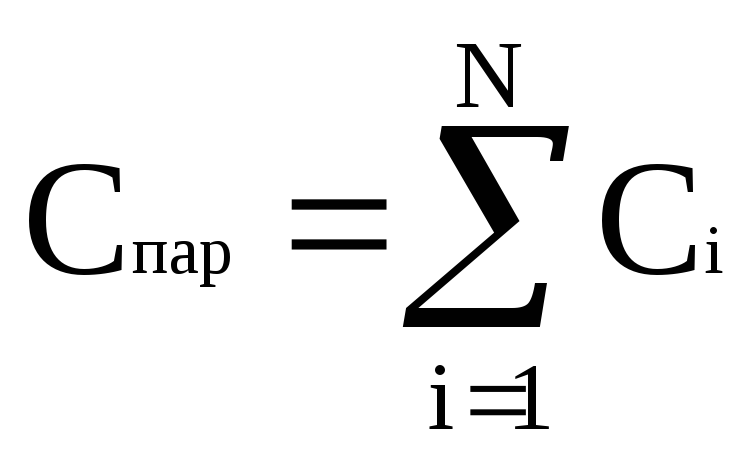ри параллельном соединении напряжение на всех конденсаторах одинаковое ( U_i = const ), а заряд батареи из N конденсатоpoв суммируется. С учетом (7) можно получить формулу емкости для батареи параллельно соединенных конденсаторов:

(8)

При последовательном соединении заряд на всех конденсаторах одинаковый (q_i =const), т.е. напряжение батареи суммируется. С учетом (7) можно получить формулу ёмкости для батареи последова­тельно соединенных конденсаторов:

(9)

Из формулы (7) следует, что емкость неизвестного конденса­тора (или батареи конденсаторов) С_х можно определить по вели­чине заряда q_x полученного конденсатором от источника тока

при постоянном напряжении:

(10)

Для определения заряда q_x в работе применяется баллистичес­кий гальванометр.