Лабораторная работа №28. Изучение процессов зарядки и разрядки конденсатора. Методичка + результаты измерений + расчеты

Цель работы: изучение процессов зарядки и разрядки конденсатора, определение

неизвестного сопротивления (или электроемкости).

Приборы и принадлежности: источник напряжения, вольтметр, микро-

амперметр, набор конденсаторов и сопротивлений, переключатель и соединительные провода.

Методика измерений:

Работа проводится на установке, схема которой представлена на рисунке.

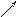
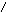
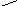
При замыкании ключа К в положение 1 происходит зарядка конденсатора С, в процессе которой пластинам конденсатора сообщаются заряды разных знаков.

При этом между пластинами конденсатора возникает электрическое поле, имеющее определенную энергию. Это поле появляется в результате действия источника тока ε, в котором сторонние силы (силы не электростатического происхождения) совершают работу по переносу зарядов против действия сил электрического поля. Количественно эта работа характеризуется электродвижущей силой.

Количество эдс - это физическая величина, численно равная работе, совершаемой сторонними силами по перемещению единичного положительного заряда по всей замкнутой цепи. Простейший способ измерения ЭДС - по напряжению на концах разомкнутого источника, то есть по показанию вольтметра, сопротивление которого намного больше, чем сопротивление источника.

В начальный момент ( t=0 ) напряжение на пластинах конденсатора отсутствует (Uc=0), и сила тока в цепи определяется равенством:

В нашем случае Rоб = R,( Rоб - общее сопротивление цепи).

П осле появления на пластинах конденсатора заряда q, сила тока в цепи уменьшается по сравнению с первоначальной, так как ЭДС частично компенсируется падением напряжения в конденсаторе. В этом случае справедливо равенство:

Г де I - мгновенное значение силы тока, Uc - мгновенное значение напряжения на конденсаторе. Учитывая, что Uc = q/C, I=dq/dt, формулу (2) можно представить в виде:

После интегрирования получим:

Из начальных условий (t=0, Uc=0) находим, что constII = - ε, откуда

И спользуя формулу (5) с формулой (2), получим зависимость разрядного тока от времени:

Сила тока имеет наибольшее значение в начальный момент времени и ассимптотически стремится к нулю в процессе зарядки. Находящаяся в цепи электрическая емкость характеризует способность проводника накапливать заряд и энергию электрического поля. Из опыта известно, что при изменении заряда проводника на величину ∆q потенциал его изменяется пропорционально заряду на величину ∆φ при этом ∆q=C∆φ (7) (С - емкость конденсатора).

Д ля того, чтобы в электрической цепи получить желаемую емкость при нужном рабочем напряжении, конденсаторы соединяют в батареи:

При параллельном соединении конденсаторов:

q=q1+q2 U=const C=C1+C2

При последовательном соединении проводников:

U=U1+U2 q=const 1/C=1/C1 + 1/C2 (10)

П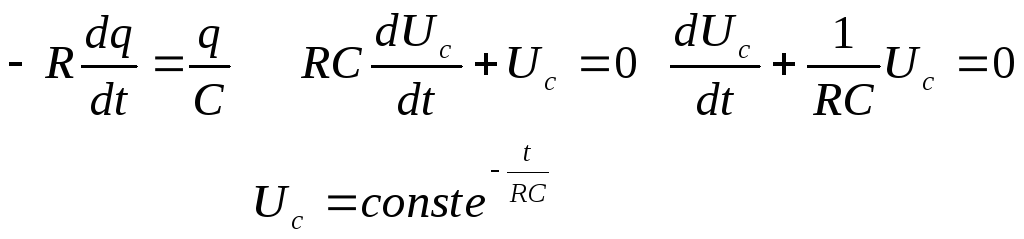 ри переброске ключа в положение 2 происходит разрядка конденсатора. Поскольку заряд конденсатора уменьшается (dq<0):

И з начальных условий (t=0, Uc=ε) находим const = ε, откуда

Разделив полученное равенство на R, получим выражение, аналогичное (6).

Величина τ = RC называется временем релаксации, по своему смыслу это интервал времени, в течение которого сила тока уменьшается в е раз.

С учетом этого зависимость силы тока от времени имеет вид:

Таблица: I x 10^-3 A [mA]

T, c	0	10	20	30	40	50	60	70	80
За рядка , I	70	66	50	36	26	20	16	12	10
	74	64	48	34	26	20	16	12	10
	72	62	46	32	24	20	14	12	8
Icp	72	64	48	34	24,6	20	15,3	12	9,3
Ln I0/I	0	0,12	0,41	0,75	1,07	1,28	1,55	1,79	2,05
Разрядка , I	68	62	48	32	26	18	14	10	8
	70	60	44	30	22	16	12	10	6
	70	60	44	30	22	16	12	10	8
Icp	69,3	60,6	45,3	30,6	23,3	16,6	12,6	10	7,3
LnI0/I	0	0,13	0,43	0,82	1,09	1,43	1,70	1,94	2,25

Графики:

<<1>> - график зависимости тока зарядки от времени.

<<2>> - график зависимости тока разрядки от времени.

<<3>> - график зависимости ln J0/Jt для тока зарядки.

<<4>> - график зависимости ln J0/Jt для тока разрядки.

Определим J0:

J0ср = (72+69.3)/2=70.65 * 10 ^-3 A

ΔJ0 = 1.35 *10^-3 A

В итоге получаем: J0 = (70.65 + - 1.35) * 10 ^ -3 A

Определим τ: - абсциссу точки, для которой значение ординаты на графиках 3) и 4) равно 1.

График <<3>>: 41,5 c График <<4>>: 39.5 c

Т.е τср = (40.5 + -1) с

Кроме того, ε = 10 В.

Зная ε и J0 определим сопротивление R: ;

R = 10 / 70.65 * 10^-3 = 141.54 Ом

; т.е. δR = 0.2/10 + 1.35/70.65 = 0.02 + 0.02 = 0.04

Т.е. ΔR = 0.04 * 141.54 = 5.66 Ом

Получаем:

R=141.54 + - 5.66 Oм

Определим емкость конденсатора и погрешность ее определения:

Т.к. , то .

С = 40.5 / 141.54 = 0.29 Ф

;

ΔC=0.06 * 0.29 = 0.02 Ф

Получаем:

С=0.29 + - 0.02 Oм

Вывод: в результате проделанной работы установили механизм протекания

процессов зарядки и разрядки конденсаторов. Используя экспериментальные данные , установили сопротивление и емкость неизвестного

конденсатора.