Занятие 6. Дифференциальные уравнения, не разрешенные относительно производной. Уравнения Лагранжа и Клеро

Цель занятия - развитие у обучающихся личностных качеств, а также направлено на овладение следующими общекультурными компетенциями:

• навыками межличностных отношений; готовностью к работе в команде;

• знаниями этических норм и использованием их в профессиональной деятельности;

• принятием различий и мультикультурности;

• способностью применять знания на практике;

• способностью приобретать новые знания, используя современные образовательные и информационные технологии;

• фундаментальной подготовкой по основам профессиональных знаний и готовностью к использованию их в профессиональной деятельности;

• навыками работы с компьютером;

• способностью к анализу и синтезу;

профессиональными компетенциями:

1) в сфере научно-исследовательской деятельности:

• умением понять поставленную задачу;

• пониманием корректности постановок задач;

• глубоким пониманием сути точности фундаментального знания;

• способностью передавать результат проведенных физико-математических и прикладных исследований в виде конкретных рекомендаций, выраженных в терминах предметной области изучавшегося явления;

• умением публично представить собственные и известные научные результаты;

• владением проблемно-задачной формой представления математических знаний;

2. в сфере проектной и производственно-технологической деятельности:

• способностью осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников;

• знанием и следование в жизни кодексу профессиональной этики;

• способностью формировать суждения о значении и последствиях своей профессиональной деятельности с учетом социальных, профессиональных и этических позиций;

• пониманием сущности и значения информации в развитии современного общества; владение основными методами, способами и средствами получения и переработки информации.

Проверка теоретических знаний

1. Дать определение изоклин для уравнения, не разрешенные относительно производной : .

(Каждая линия Ф(х, у, С) = 0 семейства есть геометрическое место точек плоскости, которым отвечает одно и то же направление касательной к интегральным кривым. Это семейство называется семейством изоклин, или семейством линий равного уклона поля направлений, определяемого исходным дифференциальным уравнением.)

2. В каком случае изоклины являются решением дифференциального уравнения?

(Если взять какую-нибудь изоклину, то в каждой ее точке дифференциальное уравнение дает одно и то же направление касательной, а именно, выбранное значение С. Для того, чтобы изоклина была решением, необходимо и достаточно, чтобы угловой коэффициент касательной к изоклине был во всех точках постоянным и равным С. Следовательно, изоклина должна быть прямой с угловым коэффициентом С, которая определяется дифференциальным уравнением в точках этой изоклины.)

3. Приведите пример уравнения, у которого изоклины являются решением.

(Примером уравнения не разрешенного относительно производной является уравнение Клеро . Семейство изоклин этого уравнения есть прямые с угловым коэффициентом С: , где С - постоянная, которая заменила у'.)

4. Существуют ли у уравнения Клеро другие решения.

(Уравнение Клеро обладает еще частным решением.)

5. Какой осуществляется подход, чтобы найти другие решения уравнения Клеро.

(Вводится замена у' = р(х).)

6. Опишите процедуру построения частного решения.

(После подстановки у' = р(х), уравнение примет вид

. (1)

Возьмем дифференциалы от обеих частей равенства

, .

Приравнивая к нулю каждый сомножитель, получаем два решения: первое - dp = 0, что дает p = C, и тем самым получаем семейство изоклин; второе определяется равенством

. (2)

Система (1), (2) дает параметрическую запись второго решения (р - параметр)

Полученное решение уравнения, не содержит произвольной постоянной, поэтому является частным решением.)

7. Дать определение особого решения.

(Решение уравнения называется особым решением, если через каждую его точку кроме этого решения проходит и другое решение, имеющее в этой точке ту же касательную, и отличное от него в любой окрестности этой точки.)

8. Дать определение огибающей семейства линий.

(Гладкая кривая называется огибающей семейства линий, если в каждой своей точке она касается кривой семейства и отлична от нее в любой окрестности этой точки, т.е. имеет в каждой своей точке касательную, общую с линией семейства, проходящей через эту же точку.)

9. В каком случае огибающая есть особая интегральная кривая уравнения.

(По теореме: если семейство решений некоторого уравнения имеет огибающую, то эта огибающая есть особая интегральная кривая уравнения.)

10. Как найти огибающую семейства решений Ф(х, у, С) = 0.

(Чтобы найти огибающую семейства решений Ф(х, у, С) = 0 некоторого уравнения необходимо найти угловой коэффициент касательной к линии семейства. Если продифференцировать Ф(х, у, С) = 0, принимая во внимание, что у есть функция от х, а С - постоянная

,

то угловой коэффициент касательной к интегральной кривой примет вид

. (3)

Так как каждая точка огибающей удовлетворяет одной из кривых семейства, то ее вид можно считать совпадающим с формулой Ф(х, у, С) = 0, считая только С не постоянной, а некоторой искомой функцией от х и у. Дифференциал от Ф(х, у, С) = 0, с учетом сказанного выше, определим формулой

. (4)

По определению угловой коэффициент касательной к огибающей должен совпадать с (3). В силу этого первые два слагаемых уничтожаются, тогда третье слагаемое левой части (4) будет равно нулю

.

Так как С - функция от х и у, то dC  0, а следовательно

, (5)

это уравнение определяет С как функцию переменных х, у. Подставляя найденное С(х, у) из (5) в Ф(х, у, С) = 0, получим уравнение огибающей.

Итак, уравнение огибающей семейства можно получить исключением С из системы двух уравнений:

(6)

Полученный результат становится понятным, так как двигаясь по огибающей мы все время касаемся различных линий семейства, каждая из которых определяется своим значением С.)

11. Если для уравнения неизвестно семейство общего решения, можно ли тогда найти огибающую.

(Используя тот подход, что когда от самого уравнения мы переходили к семейству изоклин, т.е. полагали замену , в результате рассуждений пришли к необходимости решить систему (6). Выполним в (6) обратный переход, тогда огибающую для решений данного уравнения можно получить непосредственно из самого уравнение, решив систему:

) (7)

12. Какое уравнение называется уравнением Лагранжа.

(Уравнением Лагранжа называется уравнение вида , где функции (y') и (y') непрерывно дифференцируемы.)

13. К какому классу уравнение относится уравнение Лагранжа.

(Уравнение первого порядка не разрешенное относительно производной)

14. Какой метод применяется для нахождения решения уравнения Лагранжа.

(Решение этого уравнения можно найти, используя подход, примененный к уравнению Клеро. Вводя новую независимую переменную р = y'.)

15. Сколько переменных будет в равенстве после введенной подстановки.

(После подстановки будет три переменные: х, у и р.)

16. Как избавиться от одной из переменных.

(Продифференцировать равенство и сделать замену , получим

.)

17. К какому уравнению можно свести полученное уравнение.

(К линейному дифференциальному уравнению относительно функции х от аргумента р: .)

18. Если линейное уравнение решено х = f (р,С), то как запишется общее решение уравнения Лагранжа.

(Общее решение уравнения Лагранжа найдено в виде однопараметрического семейства кривых, записанное системой:

р – параметр.)

Практические задания

Пример 1. Доказать, что частное решение уравнения Клеро есть огибающая для семейства изоклин.

Решение: Нетрудно проверить, что полученное решение

уравнения Клеро является огибающей для однопараметрического семейства прямых . Проделаем процедуру, описанную в пункте 10:

1. Так как общее решение уравнения Клеро – прямые, то угловой коэффициент примет вид , откуда .

2. Найдем полный дифференциал семейства прямых: , с учетом что С – функция: .

3. Подставим в полученное равенство 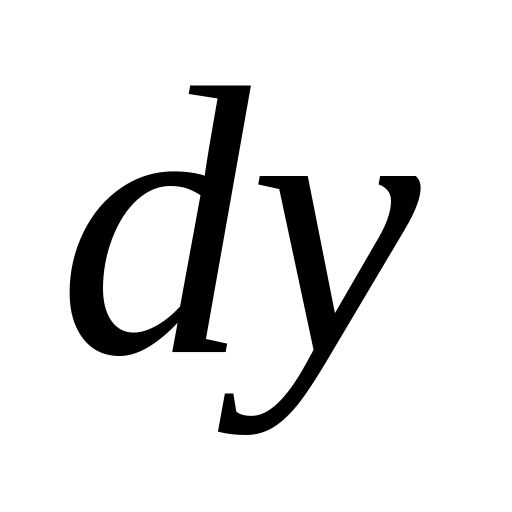: 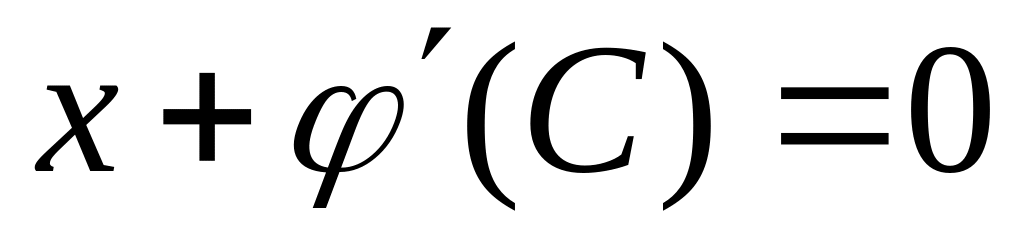или .

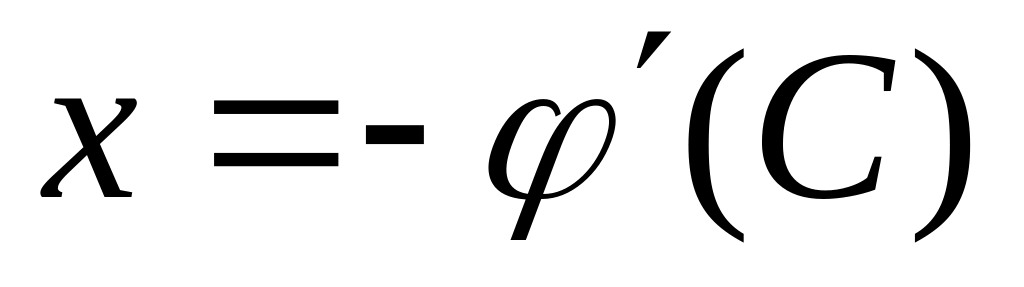4. Выражаем С и подставляем в семейство интегральных прямых, т.е. исключаем С из системы

По теореме это решение является также особым решением.

Пример 2. Найдем общее и особое решение уравнения

.

Решение: Выразим в явном виде функцию у через х и у'

.

Полагая у' = р, после подстановки в уравнение, получим и однократного дифференцирования, связь примет вид:

или

. (8)

Общий интеграл получается из , т.е.

.

Особое решение дает другая скобка равенства (8) .

Ответ: .

Пример 3. Найти огибающую семейства решений уравнения

.

Решение: Огибающая семейства решений может быть найдена из системы уравнений (7). Для этого продифференцируем исходное уравнение по

или .

Подставляя в исходное уравнение найденное значение производной, получаем параболу

у = -х²/4,

которая является решением системы (7), а следовательно огибающей для семейства решений.