2.5. Кинематический анализ механизмов с использованием графических методов.

При отыскании положений механизма графическим методом его кинематическая схема вычерчивается в выбранном масштабе К_L , в каком-либо положении начального звена.

Масштаб длин (точнее масштабный коэффициент):

Например, М 1:5 соответствует К_L=0,005 м/мм. Это значит, что 1мм на схеме соответствует 0,005 м натуральной величины.

Построение кинематических схем механизмов методом засечек, который выполняется с помощью элементарных геометрических операций.

Пример: Требуется построить план шарнирного четырёхзвенника, если заданы l_OA, l_AB, l_BC, l_OC, ω = const.

Планом механизма называется графическое изображение взаимного поло­жения звеньев, соответствующее выбранному моменту времени. Ряд следую­щих друг за другом планов позволяет наглядно проследить за движением звеньев и перемещением точек по траекториям.

Решение: Сначала показываем на чертеже положение неподвижных элементов кинематических пар: точек О и С.

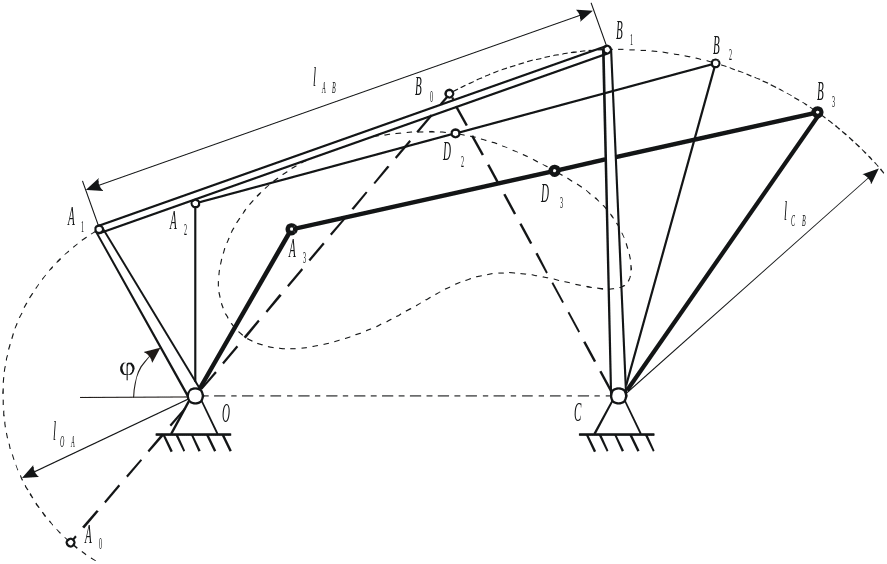
Рис 2.6. Шарнирный четырёхзвенник в нулевом, первом, втором и третьем положениях.

Затем в заданном положении изображаем начальное звено. Радиусом l_ОА вычерчиваем окружность, по которой перемещается точка А. Окружность может быть разделена на любое число равных или неравных частей. При равномерном вращении начального звена целесообразно разделить окружность на равные части, чаще всего на 8 или 12. Каждое положение точки А обозначается опре­делённым номером, который в дальнейшем присваивают плану всего механиз­ма. За нулевое положение предпочтительно принять то, при котором кривошип А₀О и шатун А₀В₀ будут лежать на одной, прямой. Это обеспечит крайнее (в нашем случае левое) положение коромысла B₀С (ведомого звена).

После этого определяем остальные положения звеньев структурной группы АВ-ВС, в частности точки B_i, делая засечки радиусом АВ из каждой точки A_i на траектории точки В. Соединив точки О, A_i, B_i, и С, получим i-ый план ме­ханизма.

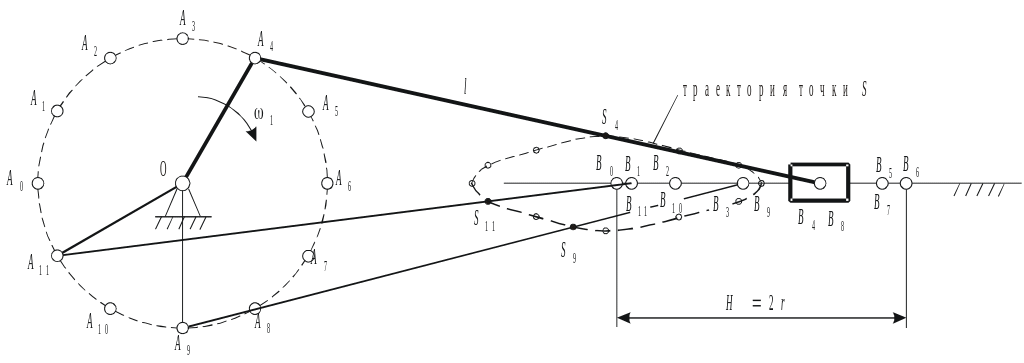
На рис. 2.3 представлена схема построения двенадцати планов кривошипно-ползунного механизма, из которых выделено три, и траектория точки S.

Рис 2.7. Кривошипно-ползунный механизм в четвертом, девятом и одиннадцатом положениях.

2.6. Распределение скоростей и ускорений в твердом

теле при плоском движении

Значительная доля механизмов, применяемых в технике относится к пло­ским. Анализ их кинематики основывается на результатах, которые получены при изучении плоскопараллельного движения.

Как известно, плоскопараллельным называется такое движение твердого тела (звена), при котором каждая его точка все время движется в одной и той же плоскости. Положение звена на плоскости (для определенности возьмем плоскость XOY) задается положением какого-либо проведенного на этом звене отрезка АВ. В свою очередь положение отрезка АВ можно определить, зная координаты x_A и y_B точки А и угол φ, который отрезок АВ образует с осью Оx . Точку А, выбранную для определения положения звена 3, будем в дальнейшем называть полюсом.

При движении звена величины x_A, y_A и φ будут изменяться. Уравнения движения звена

x_A=f₁(t), y_A=f₂(t), φ=f₃(t).

Л

Рис 2.8. Параметры, определяющие положение звена 3 на плоскости

юбое движение твердого тела c бесчисленным множеством способов можно разложить на два движения: одно переносное, другое относительное. Первые два уравнения определяют поступательное движение, при котором все точки звена движ

утся так же, как полюс А. То есть движение, которое звено совершало бы при φ=const. Его примем за переносное движение.

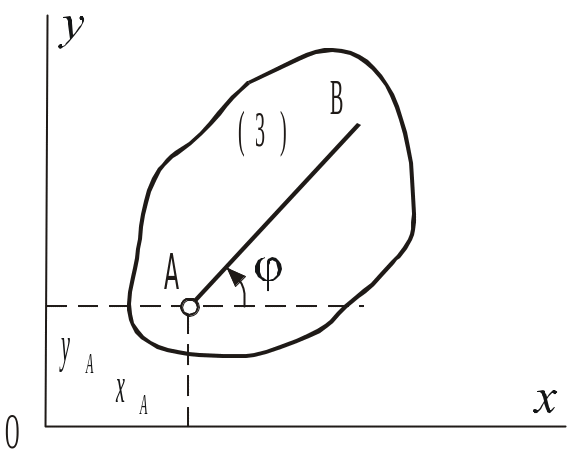
Третье уравнение определяет движение, которое звено совершало бы при x_A=const и y_A =const. Это будет вращение звена вокруг неподвижно- го полюса А.. Его примем за относительное движение.

Таким образом, в общем случае движения звена в плоскости можно рассматривать как состоящее из поступательного движения, при котором все его точки движутся так же, как и полюс А, и вращательного вокруг этого полюса. При изучении движения можно в качестве полюса выбрать любую точку звена.

Характеристики поступательного перемещения , от выбора полюса зависят. В то же время вращательная часть движения угловая скорость ω и угловое ускорение ε не зависят от выбора полюса.

Рассмотрим три ситуации, связанные с отысканием кинематических параметров подвижных звеньев механизмов.

Случай 1. Две точки принадлежат одному звену

Пусть имеется звено, на котором расположены точки А и В. Абсолютную скорость точки В представим как геометрическую сумму скоростей переносного (скорости полюса ) и относительного (скорости вращения точек вокруг полюса А - ) движений.

Р

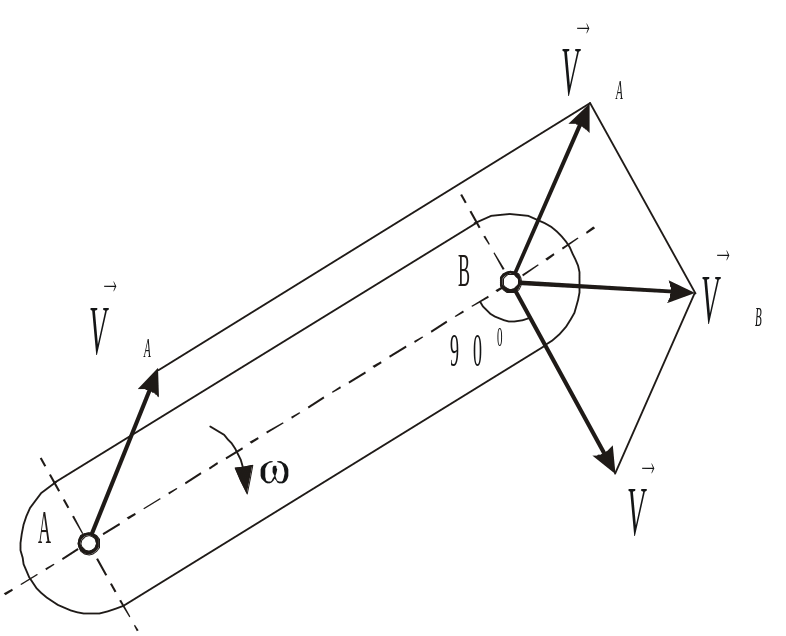
Рис 2.9. Скорости точек жесткого звена.

ешение векторного уравнения представлено на рис. 2.9. Следует иметь в виду, что и модуль этого вектора определяется по формуле , где ω - угловая скорость звена. Направление ω можно определить по направлению и наоборот. Например, когда известно направление , то следует мысленно перенести вектор в точку В и посмотреть, куда стремиться переместиться точка В вокруг точки А.

Изображение скоростей в виде пучка векторов, при котором абсолютные скорости точек звеньев выходят из одной точки, а относительные скорости соединяют концы лучей, называют планом скоростей.

Поскольку переносное движение выбрано поступательным, то ускорение точки В можно представить в виде геометрической суммы двух ускорений .

У скорение разложим на два: нормальное направленное от точки В к точке А, и тангенциальное, направленное перпендикулярно линии АВ.

Окончательно получаем следующее векторное уравнение для отыскания ускорения точки В:

Рис 2.10. Ускорение точек жесткого звена.

.

Величина ускорения и определим по формулам:

и ,

где ε - угловое ускорение звена. Направление ε можно определить по направлению, а ^τ_ВА и наоборот.

Случай 2. Теоремы подобия для планов скоростей и ускорения

2.1. Дано. 1. Линейные размеры звена CDE.

a)

б)

2. и скорости точек C и D.

План скоростей

б)

а)

а

б

Требуется определить .

С

Рис 2.11. Определение скоростей точек одного звена.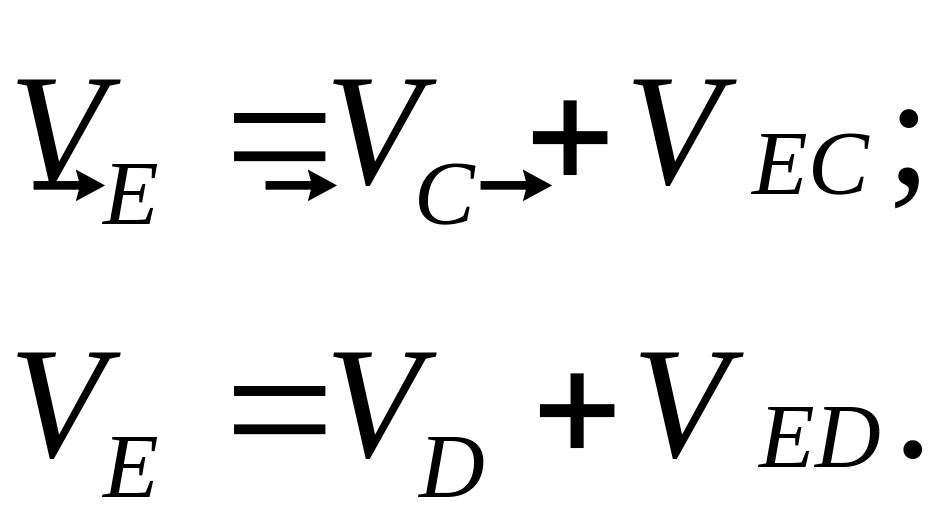

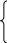
корость связана со скоростями и уравнениями:

Строим план скоростей. Треугольник CDE подобен треугольнику cde

, поскольку и .

Это свойство позволяет сформулировать теорему подобия для плана скоростей: относительные скорости точек жесткого звена образуют на плане скоростей фигуру подобную самому звену и повернутую на 90 ° в направлении его угловой скорости. В подобных фигурах соответствующие стороны пропорциональны

.

В случаях, когда известны скорости двух точек звена, скорости всех остальных точек звена следует искать с помощью теоремы подобия. Необходимо иметь в виду, что при обходе вершин углов подобных фигур на звене и на плане скоростей в одном и том же направлении, например по часовой стрелке, последовательность расположения букв должна быть одинаковой.

2.2. Дано: 1. Линейные размеры звена CDE,

2. и ускорения точек С и D.

План ускорений.

Требуется определить: .

a)

б)

Рис. 2.12. Определение ускорений точек одного звена.

При решении задач на отыскание ускорений предполагаем, что все скорости известны. Ускорение связано с ускорением и зависимостями:

,

где ; .

,

где ; .

Строим план ускорений. Полные относительные ускорения могут быть найдены по известным из механики формулам:

, поскольку их соответствующие стороны пропорциональны.

Это свойство позволяет сформулировать теорему подобия для плана ускорений: полные относительные ускорения точек жесткого звена образуют на плане ускорений фигуру подобную самому звену (при одинаковом направлении обхода фигур чередование букв при вершинах должно быть одинаковым).

.

Случай 3. Две точки совпадают в данный момент времени, но принадлежат различным звеньям, которые образуют между собой поступательную пару.

П

Рис 2.13. Кинематика звеньев, образующих между собой поступательную пару.

a)

б) план скоростей

в) план ускорений

г)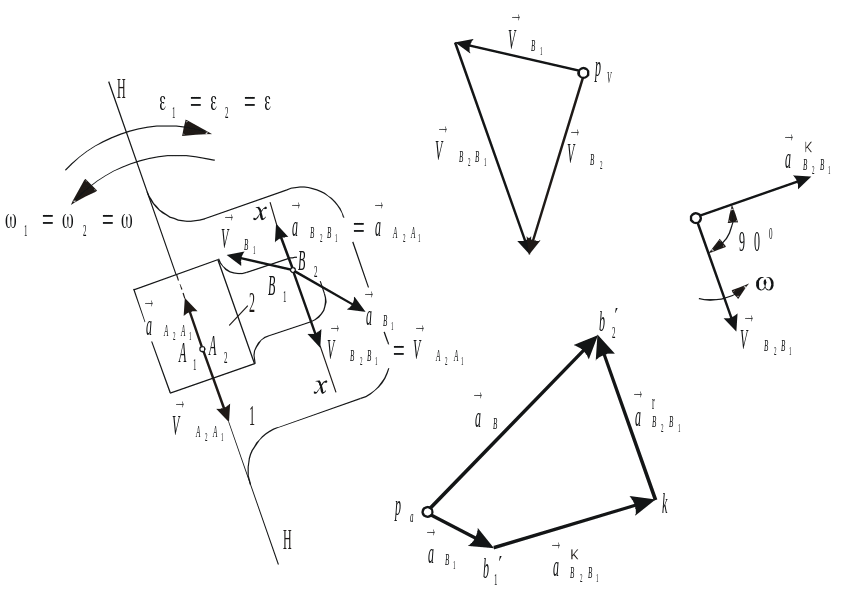

усть звенья 1 и 2 образуют поступательную пару с направляющей "НН". Произвольно выбранные точки A₁ и B₁ принадлежат звену 1 и в

данный момент совпадают соответственно с точками А₂ и В₂ расположенными на звене 2. В нашем случае точка А₂ расположена над точкой А₁, и точка В₂ над B₁.При составлении векторных уравнений будем основываться на следующих соображениях:

3.1. Без ущерба для общности за переносное движение принимаем движение звена 1. Заметим, что с равным успехом можно было бы за переносное принять движение звена 2. Для точки А переносной будет скорость , для точки В - . В общем случае .Но относительные скорости точек А₂ и В₂ при движении звена 2 по направляющей "HH" совпадают , поскольку точка B₂ перемещается по прямой линии "XX" ||"HH". Следовательно ;

3.2. Так как звенья 1 и 2 образуют поступательную пару, то относительное вращение между ними отсутствует. Поэтому: и .

3.3 Переносные ускорения точек А и В в общем случае не совпадают , но относительные ускорения равны по величине и направлению .Абсолютное ускорение точки В₂ может быть найдено из уравнения:

,

где - кориолисово (поворотное) ускорение. Оно появляется в результате изменения направления относительной скорости и определяется в плоском движении по формуле: , где ω=ω₁=ω₂ угловая скорость переносного движения, - относительная скорость.

Направление ускорения можно получить по правилу Н.Е. Жуковского. Для этого следует вектор относительной скорости повернуть на 90° вокруг оси, параллельной оси переносного вращения в сторону вращения, обусловленного угловой скоростью ω.

2.3. Определение скоростей и ускорений групп 2-го класса методом планов. Смотри таблицу 2.1.