Глава 2. Кинематический анализ плоских рычажных механизмов

Лекция 3-4

Кинематическое исследование состоит в изучении движения звеньев механизма с геометрической точки зрения, то есть без учета их инертности (массы) и действующих на них сил.

При анализе решаются три основные задачи:

1. определение положений звеньев и траекторий, описываемых отдельными точками звеньев;

2. определение линейных скоростей отдельных точек и угловых скоростей звеньев;

3. определение линейных ускорений отдельных точек и угловых ускорений звеньев.

Здесь считаются известными (заданными) кинематическая схема механизма, размеры звеньев и законы движения начальных звеньев.

Методы кинематического исследования:

графический (построение планов скоростей и ускорений или кинематических диаграмм) и аналитический. Графические методы исследования универсальны, давая достаточную для инженерной практики точность, оказываются нагляднее и проще аналитических. Однако графические методы не всегда обеспечивают достижение достаточного уровня удобств при углублённом всестороннем исследовании параметров механизма.

Рис. 2.1. Законы движения начальных звеньев, заданных в форме функций перемещения.

Начальное звено может образовывать со стойкой вращательную или посту­пательную кинематические пары, следовательно, закон движения начального звена может быть задан в виде функции ω=ω(t) или s=s(t). Обычно на практике в нулевом приближении считают движение начального звена равномерным.

2.1. Задача о положениях

Является первой при анализе кинематики механизма.

Линейные и угловые размеры звеньев кинематической схемы отнесём к постоянным параметрам, к переменным параметрам — линейные и угловые величины, определяющие положения подвижных звеньев относительно стойки и относительно других подвижных звеньев. Конкретный выбор параметров и их число зависят с одной стороны от принятого способа параметризации, а с другой от содержания задачи его кинематического анализа.

В качестве примера рассмотрим постоянные и переменные параметры двух плоских механизмов: шарнирного четырёхзвенника и кривошипно-ползунного (см. рис. 2.2).

а)

б)))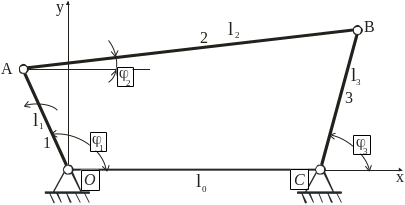

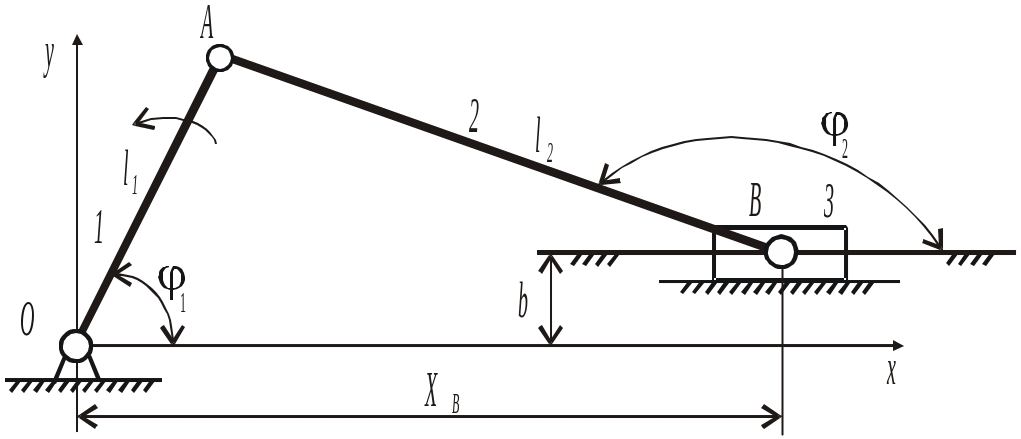
Рис. 2.2. Шарнирный четырёхзвенник (а) и кривошипно-шатунный механизм (б)

Механизм	Постоянные параметры	Переменные параметры
Шарнирный четырёхзвенник	l0, l1, l2, l3	, ,
Кривошипно-ползунный	l1, l2, b	, , Xb

Функцией положения механизма называют зависимость координаты выходного звена от обобщённых координат механизма. Для определённости примем, что звено i совершает вращательное или поступательное движение, описываемое одной координатой

,

где - функция положения звена i; - обобщенная координата механизма (координата начального звена).

Очевидно, что размерность функции положения совпадает с размерностью координаты  .

Если положение звена относительно стойки определяется k координатами (параметрами), то вводится k функций положения.

Функции положения можно ввести для каждого подвижного звена.

Например, для механизма на рис. 2.2 (а) W=1, обобщённая координата .

Если рассматривать звено 3 (k = 1), функция положения ; если рассматривать звено 2 (k = 3), функция положения .

Для механизма на рис. 2.2 (б) W=1, обобщённая координата . Если рассматривать звено 3 (k = 1), то .