6.3 Кратчайший путь. Алгоритм Дейкстры

6.3.1. Алгоритм Дейкстры

Этот алгоритм применяют для графов с неотрицательными весами, т.е. W(l),l– ребро(дуга).

Весовая матрица

Пусть UиV- вершины графа, тогда:

W(U,V)=(6.4)

Пусть S– начальная вершина,t– конечная вершина.

В течении работы алгоритма каждой вершине Vприсваивается значениеd(V) равное расстоянию от вершиныSдоV.

Перед началом работы алгоритма строится весовая матрица и значение d(V) совпадает с весом дуги (S,V) если такая существует или равнав противном случае.

Мы будем проходить вершины орграфа и уточнять значение d(V). На каждом шаге алгоритма отмечается одна вершинаU, до которой уже найден кратчайший путь отSи расстояниеd(U) до неё. Далее полученное значениеd(U) отмеченной вершины не меняется.

Для оставшихся неотмеченных вершин Vчислоd(V) будет меняться с учетом того, что искомый кратчайший путь до них от вершиныSбудет проходить через последнюю отмеченную вершинуU. Алгоритм завершается в тот момент, когда все возможные вершины будут отмечены и получат свои окончательные значенияd(V).

Пример 7.

Рис.14

Весовая матрица:

	S	A	B	C	D	E	F	T
S	0	5	10	4	∞	∞	∞	∞
A	∞	0	4	∞	10	∞	13	∞
B	∞	∞	0	∞	∞	∞	8	∞
C	∞	∞	6	0	10	18	14	∞
D	∞	∞	∞	∞	0	6	∞	12
E	∞	∞	∞	∞	∞	0	∞	5
F	∞	∞	∞	∞	∞	3	0	9
T	∞	∞	∞	∞	∞	∞	∞	0

Решение:

Шаг	Отмеч.вершины	Расстояние до вершин								Неотм.вершины
		S	A	B	C	D	E	F	T
0	S	0	5	10	4	∞	∞	∞	∞	A,B,C,D,E,F,T
1	C	0	5	10	4	14	22	18	∞	A,B,D,E,F,T
2	A	0	5	9	4	14	22	18	∞	B,D,E,F,T
3	B	0	5	9	4	14	22	17	∞	D,E,F,T
4	D	0	5	9	4	14	20	17	26	E,F,T
5	F	0	5	9	4	14	20	17	26	E,T
6	E	0	5	9	4	14	20	17	25	T
7	T	0	5	9	4	14	20	17	25	-

Шаг 0: отмечаем начальную вершину и в поле «Расстояние до вершин» переписываем первую строку весовой матрицы. В поле «Неотмеченные вершины» записываем оставшиеся вершины. Затем ищем в поле «Расстояние до вершин» минимальное число, в данном примере 4, соответственно помечаем вершину С и больше не изменяем в данном столбце значение.

Шаг 1. В поле «Отмеченные вершины» записываем вершину С. Из вершины С в вершину А нет пути, поэтому оставляем значение 5 в столбце А без изменения, из вер.С в вершину В есть путь, равные 6, но т.к. на предыдущем шаге мы отметили вершину С и длину пути 4, то искомое значение в столбце В будет получено следующим образом –(6+4)=10.

Из вершины С в вершину Dсуществует путь равный 10, соответственно искомое значение равно (10+4)=14 и т.к. оно меньше, чем ∞, то заносим его в таблицу. Аналогично для других вершин. Теперь ищем минимальное значение в строке С и подчеркиваем его(в примере – 5). В поле «Неотмеченные вершины» записываем все вершины, кроме тех, которые находятся в поле «Отмеченные вершины». Теперь помечаем вершину А.

Шаг 2,3,4,5,6,7 аналогичны шагу 1.

Затем получен кратчайший путь, соответвующий:

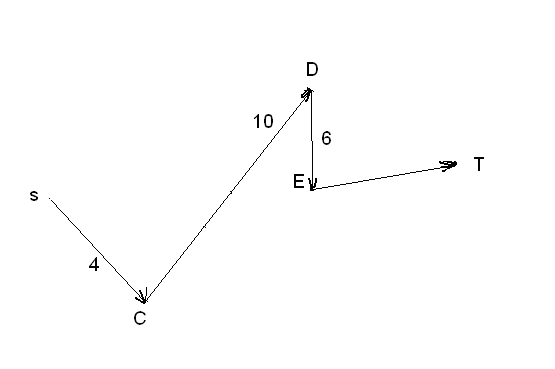
Рис.15

или:

Рис.16