
- •6. Методы решения задачи поиска кратчайшего пути
- •6.1. Нахождение кратчайшего пути
- •6.1.1. Прямой симметричный алгоритм
- •6.1.2. Задача коммивояжера
- •6.1.3. Прямой алгоритм (перебор с возвратом).
- •6.1.4. Алгоритм Дейкстры.
- •6.1.5. Алгоритм Литтла.
- •1) Зануление по строкам
- •2) Зануление по столбцам
- •6.2. Основные понятия и определения динамического программирования
- •6.2.1. Жадный алгоритм.
- •6.3 Кратчайший путь. Алгоритм Дейкстры
- •6.3.1. Алгоритм Дейкстры
- •6.4. Сетевое планирование
- •6.4.1. Правила построения сетевого графика
- •6.4.2. Алгоритм построения сетевого графика
- •6.4.3. Метод Фалкерсона
- •6.4.4. Временные параметры сетевых графиков
- •6.4.5. Пример построения сетевого графика
- •6.4.6. Пример расчета временных характеристик
- •Оглавление
6. Методы решения задачи поиска кратчайшего пути
6.1. Нахождение кратчайшего пути
Задача нахождения кратчайшего пути имеет две формулировки:
• найти кратчайший разомкнутый путь;
• найти кратчайший замкнутый путь.
Для решения каждого варианта задачи созданы специальные алгоритмы. Наибольший интерес представляет задача о поиске кратчайшего замкнутого пути, при условии, что требуется посетить все указанные пункты маршрута хотя бы по 1 разу.
6.1.1. Прямой симметричный алгоритм
Этот алгоритм применяется для нахождения кратчайшего разомкнутого пути. Суть алгоритма состоит в том, что, начиная от стартовой вершины рассматриваются альтернативные пути движения к вершине финиша. Если при рассмотрении альтернативных путей нарушается принцип симметричности, то «несимметричный» путь отбрасывается (далее не анализируется). С помощью этого алгоритма решают некоторые задачи оптимального планирования по одному параметру без вычисления временных Параметров сетевого графика. Подробно работу алгоритма рассмотрим на примере.
Пример 1. Проложить водопроводные трубы между девятью объекта кратчайшим (в экономическом смысле) путем. Объект 0 — водонапорная башня. Данные приведены на рисунке, где на ребрах графа — стоимость работ по прокладке водопровода на данном участке (ребре).

Рис.1
Введем следующие обозначения.
dj — стоимость работ по прокладке водопровода между объетами i и j.
Qj — минимальная стоимость работ от объекта 0 до объекта, т.е. Qо = 0.
Тогда Qj = min(Qj + cij).
Будем иметь:

Минимальная стоимость прокладки водопровода между пунктами
0 и 8 составит 2 + 2 + 4 = 8 и пройдет по маршруту 0-1-4-8
![]()
Рис.2
Минимальная стоимость прокладки водопровода между всеми пунктами составит: 2 + 2 + 4 + 3 + 2 + 3 + 2 + 3 = 21. Схема прокладки водопровода, соединяющего все пункты, представлена.
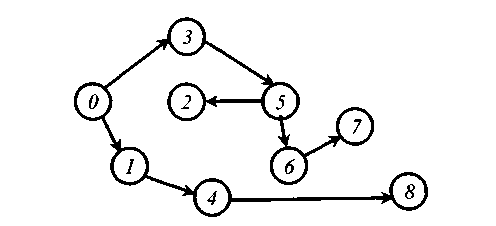
Рис.3
6.1.2. Задача коммивояжера
Задача коммивояжера имеет длинную историю. Во времена расцвета Британской империи (захвата колоний и географических открытий) англичанин У. Гамильтон придумал новую игру, суть которой состоит в том, что необходимо посетить все указанные города и вернуться назад. Такой замкнутый цикл (точка старта является и точкой финиша) называют гамильтоновым циклом. Впоследствии задача Гамильтона была уточнена и указаны пути ее решения математиками Г. Лейбницем и Я. Бернулли.
В современной интерпретации задача коммивояжера формулируется так:
В произвольном порядке обойти все вершины замкнутого графа по кратчайшему пути и вернуться в исходную вершину, причем каждая вершина проходится один раз.
В настоящее время известно несколько алгоритмов решения задачи коммивояжера, отличающиеся друг от друга эффективностью. Под эффективностью будем понимать или наименьший пройденный путь, или наименьшие затраты ресурсов (при решении экономических задач, сводимых к задаче коммивояжера).
Математическая модель задачи коммивояжера имеет вид:
![]() (6.1)
(6.1)
где п - количество вершин замкнутого графа;
Сij расстояние между городами (затраты ресурса между
работами) при наложенных ограничениях:
Cij> 0 — расстояния (ресурсы) не отрицательны;
Cjj = °° — запрет на петли внутри маршрута;
Cij = Cji —принцип симметричности (расстояние между городами одинаковое);
Cij + Cjk≥Cik —принцип треугольника (в город короче проехать напрямую, чем через третий город).
Существует масса разновидностей обобщённой постановки задачи, в частности геометрическая задача коммивояжёра (когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра.
Простейшие методы решения задачи коммивояжёра: полный лексический перебор, жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешёвого включения), метод минимального остовного дерева. На практике применяются различные модификации более эффективных методов: метод ветвей и границ и метод генетических алгоритмов.
Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time алгоритмы, то есть постепенно улучшающие некоторое текущее приближенное решение.
Задача коммивояжёра есть NP-полная задача. Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.
Класс задач NP (от Nondeterminictic Polinomial) — это класс задач, для решения которых полиномиального алгоритма может и не существовать, но если решение нам известно (например, мы его угадали), то проверить его правильность за полиномиальное время возможно (полиномиальные алгоритмы проходят за O(Nk) число операций).
Внутри этого класса принято выделять так называемые NP-полные задачи. Полиномиальные алгоритмы решения этих задач пока не найдены. Но все задачи из этого класса можно свести друг к другу. То есть, если окажется, что какая-либо из NP-полных задач решается за полиномиальное время, то это будет означать, что и все остальные задачи из этого класса эффективно разрешимы.
Острая практическая необходимость в решении NP-полных задач заставляет искать пути преодоления сложностей, связанных с их решением. В качестве таких путей можно отметить следующие: нахождение эвристических (приближенных) решений, улучшение переборных алгоритмов, динамическое программирование, использующее таблицы, размер которых экспоненциально зависит от размерности задачи. Очевидно, что последнее возможно лишь при наличии необходимого количества компьютерной памяти.
