Содержание работы

В основе метода лежит кажущееся уменьшение толщины пластинки из стекла вследствие преломления световых лучей, проходящих в стекле при рассматривании пластинки нормально к ее поверхности. В точку А, находящуюся на нижней грани пластинки, падает луч света ОА, под углом i к нормали.

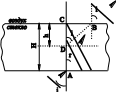
Рис. 3.1.5.

Преломившись в точке А, а затем в точке В, он выходит из пластинки под тем же углом i. Наблюдателю кажется, что рассматриваемый луч исходит не из точки А, а из точки D, т.е. толщина пластинки кажется равной СD. Из рис. 3.1.5 видно, что кажущаяся толщина СD = h меньше истинной, т.е. действительной ее толщины АС=H.

Установим связь между показателем преломления стекла n, толщиной стеклянной пластинки H и величиной кажущейся толщины пластинки h.

Показатель преломления стекла относительно воздуха

. (3.1.12)

Для лучей, близких к нормально падающим, углы падения и преломления малы, тогда синусы можно заменить тангенсами и (6) переписать:

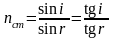. (3.1.13)

Из треугольников AВC и DBC следует

. (3.1.14)

Подставив (8) в (7), получим:

или (3.1.15)

Т.о., зная толщину пластинки H и ее кажущуюся толщину, можно определить показатель преломления стекла.

Описание оборудования

Микроскоп с микрометрическим винтом, стеклянные пластинки со штрихами на обеих поверхностях.

Порядок работы

Рис. 3.1.6

Определение кажущейся толщины пластинки производится с помощью микроскопа, снабженного микрометрическим винтом для точного измерения перемещения тубуса.

1. Устанавливают осветительное зеркальце 3 микроскопа так, чтобы поле зрения было хорошо освещено.

1. На предметный столик 1 кладется пластинка 2, на верхней и нижней поверхности которой нанесены параллельные метки, расположенные взаимно перпендикулярно.

2. Сначала микроскоп фокусируется на верхние метки, после чего записывается показание индикатора микрометрического винта. Затем микроскоп фокусируется на нижние метки и записывается новое показание индикатора. Разность показаний индикатора равна кажущейся толщине h.

3. Измеряется при помощи микрометрического винта истинная толщина стекла H.

4. По формуле: вычисляется показатель преломления стекла.

№ п/п	Толщина Н, мм	Перемещение h, мм	Показатель преломления n	Δn
1.
2.
3.
Средн.

Контрольные вопросы

1. Сформулируйте законы преломления и отражения света.

2. В чем состоит принцип Гюйгенса?

3. Выведите законы преломления и отражения света из волновых представлений.

4. В чем состоит физический смысл абсолютного и относительного показателей преломления?

5. Какая рабочая формула используется в работе?

6. Какова методика выполнения работы?

Литература

1. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. –М.: КНОРУС, 2009, 576 с.

2. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.-15-е изд., стереотип. –М.: Издательский центр «Академия», 2007. –560 с.

3. Детлаф А.А., Яворский Б.М. Курс физики. Учеб пособие для втузов. –М: Высш. Шк., 1989. –608 с.

ЛАБОРАТОРНАЯ РАБОТА № 3.4

ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ

С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА

Цель работы: изучение интерференции в тонких пленках и определение радиуса кривизны линзы.

Теоретические положения

Интерференция света

Интерференцией света называется явление такого наложения двух, или нескольких волн, в результате которого происходит перераспределение энергии волн, приводящее к усилению интенсивности света в одних местах пространства и уменьшению в других.

Рис. 3.4.1

Из электромагнитной теории Максвелла следует, что свет распространяется в виде электромагнитных волн. Как показал опыт, физиологическое, фотоэлектрическое и др. действия света вызываются колебаниями вектора напряженности электрического поля волны. Поэтому при характеристике световых колебаний пользуются только вектором .

Согласно принципу суперпозиции, световые волны, распространяющиеся от разных источников и перекрывающиеся в каком- либо месте пространства, не оказывают влияния друг на друга и напряженность результирующего колебания равна векторной сумме напряженностей складываемых колебаний.

Рассмотрим два гармонических колебания одинаковой частоты, распространяющихся от источников S₁ и S₂ и складывающихся в точке А.

; . (3.4.1)

В результате сложения возникает гармоническое колебание с амплитудой

_. (3.4.2)

Интерференция имеет место, если разность фаз  остается постоянной. Такие волны, разность фаз которых в течение времени, достаточного для наблюдения, остается постоянной, называются когерентными. Для когерентности необходимо, чтобы волны были монохроматическими, т.е. имеющими одинаковую строго определенную частоту.

Установлено, что интенсивность света I пропорциональна квадрату амплитуды световой волны:

I ~ . (3.4.3)

При сложении когерентных колебаний интенсивность результирующего колебания, исходя из (3.4.1) и (3.4.2), выразится:

, (3.4.4)

то есть результирующая интенсивность отличается от суммы интенсивностей отдельных колебаний: . Интерференция обусловлена наличием третьего члена в выражении (3.4.4), который называется интерференционным членом. Он характеризует взаимосвязь складываемых колебаний. Особенно четкой интерференционная картина будет при . Таким образом, при наложении когерентных колебаний происходит перераспределение энергии светового потока в пространстве, т.е. интерференция света.

Разность расстояний от источников колебаний до рассматриваемой точки экрана 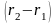называется геометрической разностью хода интерферирующих волн. Величина

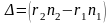(3.4.5)

называется оптической разностью хода интерферирующих волн ( и 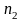- показатели преломления сред, в которых распространяются волны).

Разность фаз и оптическая разность хода интерферирующих волн связаны соотношением:

. (3.4.6)

Из (3.4.6) следует, что если  равно целому числу длин волн в вакууме:

, (k=0,1,2,3,...) (3.4.7)

то разность фаз оказывается кратной:

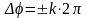. (3.4.8)

Колебания, возбуждаемые в интересующей точке экрана, происходят в одинаковых фазах, и наблюдаются максимумы результирующей интенсивности. Следовательно, (3.4.7) – условие интерференционного максимума.

Если же  равна полуцелому числу длин волн в вакууме

, (3.4.9)

,

то в точках, где разность хода слагаемых волн равна нечетному числу половин длин волн, возникающие колебания происходят в противофазе и наблюдаются минимумы результирующей интенсивности. Условие (3.4.9) – условие интерференционного минимума.

Реальные светящиеся тела испускают некогерентные волны, т.к. поверхность любого светящегося тела состоит из множества атомов, автономно излучающих цуги волн в течение времени 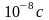, которые не связаны друг с другом фазой и направлением. При этом 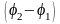непрерывно меняется, принимая с равной вероятностью любые значения. Поэтому среднее значение по времени , а результирующая интенсивность:

, (3.4.10)

т.е. при хаотическом изменении разности фаз происходит простое сложение интенсивностей, и явление интерференции не наблюдается. Только когерентные световые волны могут дать устойчивую во времени интерференционную картину.

Ограничение, налагаемое на интерференцию разностью хода, связано с длиной когерентности. Электромагнитные волны, испускаемые атомами, сохраняют постоянство амплитуды и фазы в течение ограниченного интервала времени, который называется временем когерентности . Расстояние

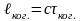, (3.4.11)

Рис. 3.4.2.

на которое распространи­лась волна за время, пока ее фаза и амплитуда оставались в среднем постоянными (~ τ_ког.), на­зывается длиной коге­рентности .

Оказалось, что если 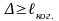, то интерференционный эффект не наблюдается, т.к. при этом соответствующие цуги не наложатся друг на друга вследствие отставания одного из них на расстояние больше . Стационарная контрастная интерференционная картина получается только при соблюдении условия

, (3.4.12)

называемого условием временной когерентности, которая обусловлена степенью монохроматичности исследуемых колебаний.

Наибольшей когерентностью обладает излучение лазера. Практически когерентные колебания можно получить делением светового пучка путем прохождения и отражения от поверхности (зеркало Френеля, бипризма Френеля, щели Юнга).