2 Фильтры с положительной ос

Ф ильтр низких частот.

Для фильтра НЧ

Частотная характеристика

Кп = F(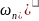

Полосовой фильтр и ФВЧ (Рисунок 5)

Частотная характеристика

Кп = F(

Расчет полосового фильтра

Очень часто при расчете фильтра полагают:

. Тогда

Расчет фильтра верхних частот

Как и для ФНЧ часто . Тогда

При K=1, если

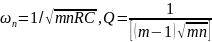
3 Фильтры с отрицательной ОС

Структурно рассматриваемые активные фильтры делятся на многопетлевые (рис. 6) и однопетлевые.

Многопетлевые активные фильтры.

Как и в предыдущем разделе фильтр содержит 2 части: пассивный шестиполбсник и усилитель.

Схема активного ФНЧ принимает вид приведенный на рис. 7.

В

Рис. 7. Фильтр нижних частот(а), его частотные характеристики (б)

практике обычно решается обратная задача – отыскание конкретных значений элементов схемы по заданным .

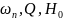Полосовой фильтр

Для реализации полосового фильтра (рис. 8), если Y1=1/R1 и Y3=pC3, то для того, чтобы в знаменателе была функция второго порядка, надо чтобы Y2=pC2, Y5=1/R5, Y6=1/R6. Схема полосовго фильтра с многопетлевой ОС приведена на рис.6.36. Здесь

.

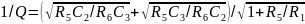
Для полосового фильтра процедура расчета элементов при заданных следующая:

Частотная характеристика

Кп = F(

Рисунок 8 – Полосовой фильтр (а) и его частотные характеристики (б)

ФВЧ реаизация фильтра высоких частот возможна при Y1=pC1, Y2=pC2, Y3=pC3, Y5=1/R5, Y=1/R6. Схема такого фильтра приведена на рис. 6.37. Здесь

.

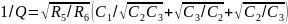
Расчет ФВЧ можно выполнить при С1=С3=С из приведенных ниже соотношений.

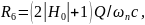
Фильтр верхних частот

Рисунок 9 – Фильтр верхних частот (а) и его частотные характеристики (б)

Частотная характеристика (Рис 9)

Кп = F(

Однопетлевые активные фильтры.

О

Рисунок 10. Обобщенная схема однопетлевого активного фильтра

бобщенная схема такого фильтра приведена на рис. 10. Фактически это схема ОБ с четырехполюсниками в качестве элементов входной цепи и цепи ОС. Обычно при реали­зации передаточных функ­ций этих четырехполюсни­ков их схемы выбирают так, чтобы полюсы входного четырехполюсника и четырехполюсника ОС совпадали. Тогда H(p)=-Nвх(p)/NОС(p), где N(p) — числители пере­даточных функций RC це­пей (табл. 1).

Первые три цепи (см. табл. 1) обеспечивают нули в начале координат или в бесконечности, поэтому их целесообразно использовать для реализации числителей передаточных функций ФНЧ, ФВЧ и полосовых фильтров. Четвер­тая и пятая цепи полезны для реализации комплексных корней как в числите­ле, так и знаменателе передаточной функции по напряжению всей цепи в це­лом.

В качестве примера Рис.11 реализацию ФНЧ с однопетлевой ОС.

Фильтры с однопетлевой ОС требуют для своей реализации большего числа схемных элементов и достаточно сложны в настройке, поскольку требуется обеспечить точное сокращение подобных членов в числителе и знаменателе передаточной функции. Однако эта схема дает возможность получать схемы с большей добротностью и более высокими статическими коэффициентами передачи