
Текст программы:
T = t(2) - t(1); %находим интервал дискретизации
w = 0:0.02:5; %задаем сетку частот, от 0 до 5 рад/с с шагом 0,02 рад/с
Sw = []; Sw_teor =[]; %обнуляем массивы
for i=1:length(w) %цикл по всем выбранным частотам
Sw(i) = sum(Rplus .* cos(w(i)*t)); %находим спектр как преобразование Фурье корреляционной функции
Sw_teor(i) = 1 / (w(i)*w(i) + 1); %теоретический спектр
Sw_h(i)=sum(Rhamm .* cos(w(i)*t)); %спектр вычисленный с использованием окна
end;
Sw = 2*T*Sw;
Sw_h = 2*T*Sw_h;
N = 2*pi/0.5/T; %считаем число точек для БПФ, чтобы шаг по частоте был равен 0,5 рад/с
N = 2^nextpow2(N); %определяем ближайшую большую степень двойки
Fw = T * fft(y, N); %выполняем БПФ
Sw_fft = Fw .* conj(Fw) / N / T; %считаем оценку спектра
Sw_fft = Sw_fft(1:N/2+1); %выделяем первую половину спектра до частоты Найквиста
w1 = 2*pi*[0:N/2] / N / T; %формируем сетку частот для графика
scale = 1 / sqrt(0.54^2 + 0.46^2/2); %находим масштабирующий коэффициент для окна Хэмминга
hamm1 = hamming(N) * scale; %строим окно Хэмминга с масштабированием
yHamm=y(1:N).*hamm1; %применяем окно к первым отсчетам сигнала
Fwh = T * fft(yHamm, N); %БПФ
Sw_ffth = Fwh .* conj(Fwh) / N / T; %считаем оценку спектра
Sw_ffth = Sw_ffth(1:N/2+1); %выделяем первую половину спектра до частоты Найквиста
figure(2);
subplot(2,1,1),
plot(w, Sw,':b','LineWidth',2),
xlabel('w'),ylabel('S')
hold on,
plot(w,Sw_teor,':g','LineWidth',2)
plot(w, Sw_h,'-r','LineWidth',2)
legend('Sw','Sw_teor','Sw_h')
xlim([0 max(w)]);
hold off
subplot(2,1,2),plot(w,Sw_teor,':g','LineWidth',2),
ylabel('S'),xlabel('w')
hold on
plot(w1,Sw_fft,'-r','LineWidth',1)
plot(w1,Sw_ffth,'-b','LineWidth',1)
legend('Sw_teor','Sw_fft','Sw_ffth')
xlim([0 max(w)]);
hold off

Рисунок 5. График экспериментальной спектральной плотности(Sw), теоретической с.п. (Sw_teor), сглаженной (Sw_h)

Рисунок 6. Графики теоретической с.п. .(Sw_teor),, и с.п. вычисленной через ДПФ с использование окна Хэмминга(Sw_ffth) и без(Sw_fft)
По рисункам 5 и 6 видно, что применение окна Хэмминга сглаживает скачкообразные изменения оценки спектра. Оценка с.п. близка к теоретической с.п. При использовании прямого метода, основанного на использовании дискретного преобразования Фурье (или в современных вычислительных алгоритмах быстрого преобразования Фурье) требуется гораздо меньше операций. При этом не нужно строить корреляционную функцию, а можно сразу найти спектральную плотность, обработав выборку значений исходного сигнала. По рисунку видно, что такой метод менее точный, и оценка не гладкая.
Используя формулу
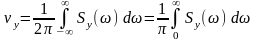 ,
,
с помощью функции trapz (численное интегрирование методом трапеций), оценим дисперсию по экспериментальному и теоретическому спектрам.
Swi=trapz(w,Sw)/pi = 0.5001
Sw_teori=trapz(w,Sw_teor)/pi = 0.4372
Дисперсии, вычисленные по экспериментальному и теоретическому спектрам, совпадают с дисперсией, рассчитанной во временной области. Это обусловлено равенством Парсеваля (сумма (или интеграл) квадрата функции равна сумме (или интегралу) квадрата результата преобразования).
