ГУАП

КАФЕДРА № 11

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

				Е.О. Логинова
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ

ИССЛЕДОВАНИЕ РАЗОМКНУТОЙ ЛИНЕЙНОЙ СИСТЕМЫ ПРИ СЛУЧАЙНЫХ ВОЗМУЩЕНИЯХ

по курсу: МЕТОДЫ ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

РАБОТУ ВЫПОЛНИЛИ

СТУДЕНТЫ ГР. №	1510М
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2016

Цель работы: освоение методов анализа одномерной линейной непрерывной системы при случайных возмущениях с помощью среды MATLAB.

Задачи работы:

• научиться вычислять среднеквадратическое отклонение и дисперсию на выходе линейной системы, возбуждаемой единичным белым шумом;

• научиться моделировать случайные процессы, используя в качестве источника сигнала белый шум (с ограниченной полосой);

• научиться оценивать СКВО и дисперсию случайного процесса, полученного при моделировании;

• научиться вычислять автокорреляционную функцию случайного процесса;

• научиться вычислять спектральную плотность случайного процесса по известной корреляционной функции;

• научиться использовать быстрое преобразование Фурье (БПФ) для оценки спектральной плотности случайного процесса;

• научиться использовать спектральные окна для сглаживания оценки спектральной плотности случайного процесса.

Краткое описание исследуемой системы:

Пусть имеется система преобразования с одним входом, на который поступает (подается) входная случайная функция X(t) – функция воздействия или возбуждения, и с одним выходом, с которого снимается выходная функция Z(t) – отклик или выходная реакция системы. Система осуществляет преобразование X(t)  Z(t) и описывается определенным системным оператором трансформации Т – функцией, алгоритмом, набором правил преобразования входного сигнала в выходной. Обозначение операции преобразования: Z(t) = T[X(t)]. Символическое и полное отображение операции преобразования:

z(t) = h(t) * x(t-t) = h(t)x(t-t) dt. (1)

где h(t) – математическая функция импульсного отклика системы на единичное входное воздействие. Импульсный отклик определяет соответствующую частотную передаточную характеристику системы: h(t)  H(w).

Для неслучайных (детерминированных) входных сигналов соотношение между выходными и входными сигналами всегда однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса (случайного сигнала) тоже существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии, ковариационной функции и пр.).

Система считается линейной, если ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия). Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.

В данной работе мы будем рассматривать разомкнутую линейную систему с передаточной функцией:

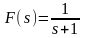(2)

Разомкнутая система – это система без обратной связи.

В качестве входного воздействия будем рассматривать белый шум. Белый шум является стационарным случайным процессом q(t), у которого автокорреляционная функция описывается дельта-функцией Дирака и, соответственно, спектральная плотность мощности не зависит от частоты и имеет постоянное значение W_q(f) = s², равное дисперсии значений q(t). Другими словами, все спектральные составляющие белого шума имеют одинаковую мощность (как белый цвет содержит все цвета видимого спектра). По существу, это идеализированный случайный процесс с бесконечной энергией. Но в случае постоянства спектральной плотности мощности случайного процесса в конечном диапазоне частот введение такой идеализации позволяет разрабатывать достаточно легко реализуемые оптимальные методы фильтрации. Многие помехи в радиотехнике, в технике связи и в других отраслях, в том числе в информатике, рассматривают как белый шум, если эффективная ширина спектра сигналов B_s много меньше эффективной ширины спектра шумов B_q

B_s/B_q << 1, (3)

и спектральная плотность мощности шумов слабо изменяется в интервале спектра сигнала. Понятие «белый шум» определяет только спектральную характеристику случайного процесса, а, следовательно, под это понятие подпадают любые случайные процессы, имеющие равномерный энергетический спектр и различные законы распределения.