Решение.

				min
	7	0	-1	-1
	5	4	-6	-6
	3	2	2	2
max	7	4	2

Для нахождения верхнего значения определим максимальное значение в каждом столбце. Затем из максимальных значений выберем минимальное.

=min(7;4;2)=2 – верхнее значение игры.

Для нахождения нижнего значения определим минимальное значение в каждой строке. Затем из минимальных значений выберем максимальное.

=max(-1;-6;2)=2 – нижнее значение игры.

= =2 – значение игры. Т.к. верхнее и нижнее значение игры совпадают, то получили ситуацию равновесия.

Ситуация равновесия: (3;3).

Ответ: Игроку 1 рекомендуется выбирать третью строку, тогда его выигрыш составит 2. В случае отклонения от оптимальной стратегии его выигрыш не увеличится. Игроку 2 рекомендуется выбирать 3 столбец, его проигрыш составит 2. В случае отклонения от данной стратегии его проигрыш не уменьшится.

Задание 4. Найти решение матричной игры Г(А) в смешанных стратегиях. (Составить пару двойственных задач. Одну из задач решить геометрически. Значение игры сравнить с верхним и нижним значениями).

А=

Решение.

1. Найдем верхнее и нижнее значение игры.

=

=3

Следовательно, решение будем искать в смешанных стратегиях. Значение игры находится в промежутке [3;4].

2. Составим пару взаимно двойственных задач.

3. Вторую задачу решим геометрически.

Построим графики функций (по оси x переменная , по оси y - переменная ). Графики представлены на рисунке 1.

(график 1).

(график 3)

(график 2)

3

1

2

G

С

Рис.1 Геометрический метод решения задачи ЛП

Выделим области, лежащие под каждым графиком (т.к. в знаке ограничений стоит <). Заштрихованная область на графике показывает область допустимым значений, т.е. тех, которые удовлетворяют заданным ограничениям. Построим функцию G.Т.к ищем максимум функции, то стрелки направлены вверх, двигаясь внутри области допустимых значений, получим, что максимальное значение достигается в точке С. Это точка пересечения графика 1 и графика 3. Для нахождения координат точки решим систему уравнений:

Получим:

Найдем значение функции F=1/3; значение игры обратно значению функции, т.е. .

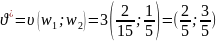
Получили оптимальную стратегию игрока 2 в смешанных стратегиях. Т.е. игроку 2 рекомендуется выбирать первый столбец с вероятностью , второй столбец – с вероятностью

Определим оптимальную стратегию игрока 1.

Игрок 1 не будет использовать свою третью стратегию ( , т.к. при этом его выигрыш меньше значения игры. Решим систему (с учетом того, что

Получим:

Тогда оптимальная стратегия игрока 1:

Вывод: игроку 1 рекомендуется с вероятностью 1 выбирать вторую строку, тогда его выигрыш составит 3. В случае отклонения от оптимальное стратегии его выигрыш не увеличится. Игроку 2 рекомендуется с вероятностью 2/5 выбирать первый столбец, с вероятностью 3/5 выбирать второй столбец, тогда его проигрыш составит 3. В случае отклонения от оптимальной стратегии проигрыш игрока 2 не уменьшится.