Задание 1. Для функции двух переменных z = f(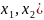 , заданной следующим выражением. а. Найти стационарную точку и вычислить в ней значение функции.

b. Найти экстремальные точки и экстремальные значения.

c. Найти области выпуклости (вогнутости) функции.

Решение

1. Необходимое условие экстремума функции: если y – точка экстремума, то она является стационарной точкой.

В стационарной точке частные производные равны 0. Найдем частные производные функции.

2. Решив систему, получим: , - координаты стационарной точки.

- значение функции в стационарной точке.

3. Для нахождения экстремума составим матрицу Гессе, элементы которой являются вторыми частными производными функции.

Найдем угловые миноры и проверим их знак.

220>0

Т.к. угловые миноры положительны, то матрица Гессе положительно определенная, а найденная стационарная точка является точкой минимума функции. Функция выпуклая.

Ответ: точка с координатами , является точкой минимума функции. Экстремальное значение равно 9,841.

Задание 2. Функция трех переменных u = f(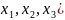 , заданной следующим выражением. а. Найти стационарную точку и вычислить в ней значение функции.

b. Найти экстремальные точки и экстремальные значения функции.

c. Найти области выпуклости (вогнутости) функции.

Решение

1. Найдем стационарную точку функции. Для этого вычислим частные производные.

Приравняем частные производные к 0. Решив систему, найдем координаты стационарной точки.

Значение функции f(-0.485,-0.121,-0.242)=0.379.

2. Для нахождения точки экстремума составим матрицу Гессе. Найдем вторые производные.

Найдем значения вторых производных в стационарной точке и составим матрицу :

Определим знак угловых миноров.

|3.792|>0

>0

<0

Т.к. угловые миноры меняют знак, то данная стационарная точка является седловой. Экстремума функции нет.

Ответ: Значение функции в стационарной точке f(-0.485,-0.121,-0.242)=0.379. Точка является седловой, экстремума нет.

Задание 3. Дана функция 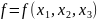и ограничения. а. Составить функцию Лагранжа.

b. Найти стационарную точку функции Лагранжа.

c. Найти условный экстремум функции 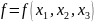(экстремальную точку, экстремальное значение и тип экстремума).

1. Составим функцию Лагранжа, которая имеет вид: .

2. Найдем стационарную точку функции Лагранжа. Для этого найдем частные производные функции и приравняем их к 0.

Координаты стационарной точки функции Лагранжа: (0.607,3.325,0.209,-6.477,-14.198).

3. Для нахождения экстремума составим матрицу Гессе. 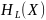, которая имеет вид:

, где -ограничение.

=

M=2

2*M+1=5

Определим знак 2*М+1 минора.

Знак углового минора совпадает со знаком , следовательно, найденная стационарная точка является точкой минимума.

4. Значение функции в точке экстремума равно 40.398. Это значение является минимальным и достигается в точке (0.607, 3.325, 0.209).

Ответ: Координаты стационарной точки функции Лагранжа: (0.607,3.325,0.209,-6.477,-14.198). Эта точка является точкой минимума, экстремальное значение равно 40.398.

Задание 4. Составить математическую модель и найти оптимальное решение, используя процедуру «Поиск решения» MS Excel.

Процесс изготовления двух видов изделий состоит в последовательной обработке каждого изделия на трех станках. Время использования станков ограничено 10 ч в сутки. Время обработки и прибыль от продажи одного изделия указаны в таблице. Найти оптимальные объемы производства.

Таблица

Изделие	Время обработки 1 изделия, мин			Удельная прибыль
	Станок 1	Станок 2	Станок 3
1	10	6	8	2$
2	5	20	15	3$