1, 2 ‒ Начальное и конечное состояния горячего теплоносителя;

3, 4 ‒ Начальное и конечное состояния холодного теплоносителя

Рисунок 23. 1 ‒ T-S- диаграмма процесса теплообмена в

противоточном аппарате

Для простоты расчетов примем G_Г=G_Х, с_рГ=с_рХ=с_р. Тогда

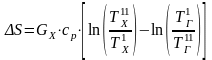. (23.2)

Расход холодного теплоносителя выразим из уравнения теплового баланса

. (23.3)

Обозначим ; ; 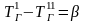; ; 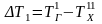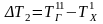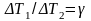. Тогда

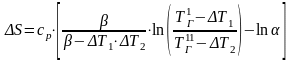. (23.4)

Средняя движущая сила процесса есть средняя логарифмическая разность температур

, (23.5)

из чего следует

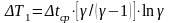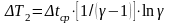; ; (23.6)

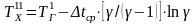; ; (23.7)

. (23.8)

Из последнего выражения видно, что ΔS минимально при 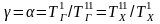. Тогда

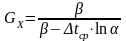. (23.9)

В этом случае прирост энтропии системы в процессе теплообмена и, следовательно, эксергетические потери в аппарате будут минимальны. В соответствии с уравнением Гюи-Стодолы их можно оценить как

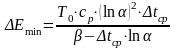. (23.10)

Эксергетический КПД теплообменника при этом будет максимальным

, (23.11)

где 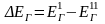‒ уменьшение эксергии теплоносителя, отдающего тепловую энергию в аппарате.

Таким образом, для всех рабочих веществ эксергетические потери будут минимальными при отношении разностей температур теплоносителей на концах поверхности теплообмена, равном отношению граничных температур, т. е. при соблюдении условия

. (23.12)

В этом режиме эксергетические потери являются функцией только среднего температурного напора. Любое отклонение от этого условия приводит к увеличению прироста энтропии системы, особенно с повышением среднего температурного напора.

Для случая, когда теплоносителями являются разные вещества с разными давлениями в потоках оптимальные значения температур холодного теплоносителя можно вычислить по уравнению (23.7) с учетом (23.12), а эксергетические потери рассчитать при этих оптимальных температурах.

Минимальное изменение энтропии в противоточном теплообменнике в общем случае зависит от кинетики процесса, теплофизических свойств и температурных характеристик теплоносителей

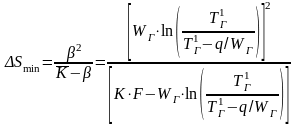, (23.13)

где 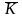, К ‒ соответственно эффективный и средний коэффициенты теплопередачи; F ‒ площадь поверхности теплообмена; 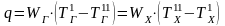‒ суммарное количество передаваемого в аппарате тепла; W_Г, W_Х ‒ водяные эквиваленты горячего и холодного теплоносителей.

Зависимость минимального изменения энтропии от удельной тепловой нагрузки аппарата носит экстремальный характер (рисунок 23.2).

Рисунок 23.2 ‒ Зависимость минимального изменения энтропии от

удельной тепловой нагрузки

На практике, как правило, возникает необходимость в поддержании на постоянном уровне выходной температуры одного из потоков. В этом случае тепловая нагрузка зависит от входной температуры и водяного эквивалента этого потока. Для того чтобы при фиксированной тепловой нагрузке теплообменник работал в термодинамически оптимальных условиях, т. е. с минимальным изменением энтропии, достаточно выполнение равенства

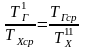. (23.14)

Данное условие характеризует постоянство отношений температур теплоносителей в любом сечении аппарата. В этом случае теплообменник работает в термодинамически оптимальном режиме при любых тепловых нагрузках.

Для оценки термодинамического совершенства работы теплообменника можно использовать показатель энтропийного КПД

, (23.15)

где ΔS_Д ‒ действительное изменение энтропии в теплообменнике.

Если теплообмен протекает в условиях, близких к изобарным, т. е. гидравлическое сопротивление аппарата невелико, то для идеального и большинства реальных газов действительное изменение энтропии определяют по параметрам потоков на входе и выходе теплообменника

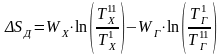. (23.16)

Перераспределяя массовые расходы потоков, можно изменять термодинамическую эффективность работы теплообменника, что отражается непосредственно на водяных эквивалентах потоков. Для приближения параметров процесса к оптимальным значениям устанавливают дополнительные теплообменники на прямом и обратном потоках, используют прием байпасирования потоков, дополнительный подвод теплоносителей и т. д.

Целесообразность использования эксергетического или энтропийного КПД определяется целями проводимого анализа и особенностями работы аппарата. В тех случаях, когда теплообменник является самостоятельным агрегатом и интерес представляет совершенство протекающих в нем процессов, или же когда необходимо сравнить два теплообменника разных конструкций, работающих при одинаковых начальных параметрах, наиболее удобным критерием оценки является энтропийный КПД. Если же теплообменник является частью какой-либо системы и его работу оценивают как работу одного из элементов этой системы с помощью эксергетического КПД.

Параграф 24. Эксергетический анализ выпарных установок.

На практике наиболее часто выпаривают водные растворы, теплоносителем при этом служит водяной пар. Скорость процесса определяется скоростью подвода тепла к раствору. Следовательно, при выпаривании, как и при всех тепловых процессах, часть подведенной эксергии безвозвратно теряется вследствие необратимости протекающих в установке процессов теплообмена.

Для удаления из исходного раствора N молей растворителя при постоянной температуре необходимо совершить работу, равную теплоте дегидратации растворенного вещества в соответствующем диапазоне изменения концентрации раствора в процессе выпаривания. Эксергия системы при этом изменится на величину

, (24.1)

где Q_ДЕГ ‒ теплота дегидратации растворенного вещества в соответствующем диапазоне изменения концентрации раствора в процессе выпаривания (затрата тепла на повышение концентрации раствора); Т_СТ ‒ температура стабилизации раствора, т. е. температура, при которой энергия Гиббса не изменяется вследствие взаимодействия между компонентами раствора, сопровождаемого тепловым эффектом (для водных растворов Т_СТ=647 К); N_ср ‒ средняя мольная доля растворителя в растворе

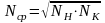, (24.2)

где N_Н, N_К ‒ начальная и конечная мольные доли растворителя в растворе.

Таким образом, минимально необходимый (теоретический) расход эксергии в процессе выпаривания не зависит от условий его проведения, а определяется лишь потоком выпариваемого раствора, его свойствами и диапазоном изменения концентраций.

Однако в реальном процессе возникают дополнительные статьи расхода эксергии, обусловленные снижением температурного потенциала пара за счет температурных депрессий (физико-химической, гидростатической, гидравлической). Эти потери эксергии можно определить следующим образом. Для повышения эксергетического потенциала пара за счет его сжатия необходимо затратить работу

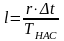, (24.3)

где r ‒ удельная теплота парообразования исходного раствора; Т_НАС ‒ температура насыщенных паров над кипящим раствором; Δt ‒ полезная разность температур в процессе.

Расходуемая на сжатие работа превращается в теплоту, эксергия которой при данной температуре равна

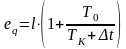, (24.4)

где Т_К ‒ температура кипения исходного раствора.

За вычетом этой эксергии работу, затрачиваемую на компенсацию понижения температуры пара за счет температурных депрессий, определяют как

. (24.5)

Расход эксергии на нагревание раствора в выпарном аппарате до температуры кипения равен

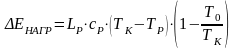, (24.6)

где L_Р ‒ расход исходного раствора; Т_Р ‒ начальная температура исходного раствора; с_Р ‒ удельная теплоемкость исходного раствора.

Фактический расход эксергии греющего пара на выпаривание раствора в однокорпусной выпарной установке непрерывного действия составляет

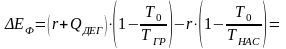
, (24.7)

где Т_ГР ‒ температура греющего пара.

Для оценки эффективности работы однокорпусных выпарных установок используют значение их эксергетического КПД, которое определяют как отношение минимально необходимой (теоретической) затраты эксергии к ее фактическому расходу

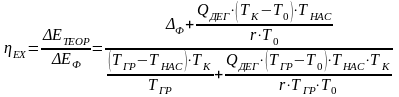, (24.8)

где Δ_Ф ‒ физико-химическая температурная депрессия.

Если энергетический потенциал вторичных паров не используют, то их эксергию можно не принимать во внимание и считать, что Т₀=Т_НАС, а . Тогда выражение для расчета эксергетического КПД заметно упростится

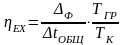, (24.9)

где 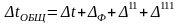‒ общая разность температур в подогревателе исходного раствора; Δ¹¹, Δ¹¹¹ ‒ соответственно гидростатическая и гидродинамическая температурные депрессия.

Приведенные выражения для расчета эксергетического КПД однокорпусных выпарных установок справедливы и для многокорпусных установок, эксергетический КПД которых определяют в этом случае как среднее значение показателя по отдельным корпусам. Этот КПД зависит от температуры исходного раствора перед первым корпусом. На практике исходный раствор, как правило, подогревают до температуры его кипения, снижая тем самым эксергетический КПД установки. Влияние это тем сильнее, чем большее количество исходного раствора приходится на единицу выпариваемого растворителя.

Параграф 25. Термоэкономический метод оптимизации рабочих параметров выпарных установок.

Эффективность работы выпарной установки в значительной степени определяется числом последовательно соединенных корпусов. В связи с этим, выбор их оптимального числа, так же как и оптимальных параметров их работы, представляет собой важную и актуальную задачу. На практике процесс выпаривания растворов сопровождается не расходом эксергии теплоносителя, используемого в установке, а снижением эксергетического уровня почти постоянного теплового потока. Это относится как ко всему процессу в целом, так и к каждой из его стадий ‒ теплообмену, собственно процессу разделения исходного раствора на готовый продукт и растворитель, компенсации гидростатической и гидродинамической температурных депрессий, подогреванию исходного раствора до температуры кипения.

Затраты, связанные с обеспечением работы отдельного корпуса выпарной установки, равны

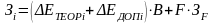, (25.1)

где З_i ‒ удельные затраты на 1 моль выпариваемого растворителя в i-ом корпусе выпарной установки; ΔЕ_ДОПi ‒ уменьшение эксергии теплового потока в i-ом корпусе, обусловленное снижением его температурного уровня в процессе теплообмена

, (25.2)

где Q_ИСП ‒ теплота испарения растворителя; Т ‒ температура процесса выпаривания;

В ‒ стоимость эксергии; F ‒ удельная поверхность теплообмена; З_F ‒ затраты, связанные с обеспечением необходимой для протекания процесса теплообменной поверхности.

С достаточной для практических целей точностью температуру раствора, поступающего в рассматриваемый корпус, можно принять равной температуре кипения в нем, а затратами эксергии на компенсацию гидростатической и гидродинамической температурных депрессий в первом приближении пренебречь. Тогда

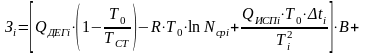
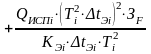, (25.3)

где К_Эi, Δt_Эi ‒ соответственно коэффициент теплопередачи и средняя движущая сила процесса в эталонных условиях в i-ом корпусе выпарной установки.

Оптимальное значение полезной разности температур соответствует минимальному значению полученного выражения. Для нахождения этого минимума этой функции необходимо приравнять нулю ее первую производную, после чего получим выражение для определения оптимальной полезной разности температур в i-ом корпусе

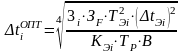, (25.4)

где Т_Эi ‒ температура процесса выпаривания в эталонных условиях в i-ом корпусе выпарной установки.

При принятых допущениях оптимальная полезная разность температур в отдельном корпусе выпарной установки не зависит от температуры кипения раствора в нем.

Проанализируем схему прямоточной многокорпусной выпарной установки с тепловым насосом ‒ устройством, повышающим температурный уровень теплоты, выделяющейся в процессе выпаривания (рисунок 25.1). Между температурой греющего пара и температурой кипения раствора в многокорпусных установках поддерживается разность температур всего в несколько градусов. Сжимая адиабатически вторичный пар в термокомпрессоре, можно повысить его температуру насыщения до необходимой для получения нужной разности температур и передачи кипящему раствору тепла в выпарном аппарате. При этом в самом выпарном аппарате испаряющееся количество воды приблизительно равно количеству расходуемого первичного пара, следовательно, применяя сжатие вторичного пара, можно теоретически обойтись одним этим паром, без добавления свежего. Перед пуском аппарата раствор должен быть подогрет свежим первичным паром, который вводят до начала кипения жидкости. После чего прекращают подачу греющего пара и ведут процесс за счет теплоты сжимаемого в термокомпрессоре вторичного пара. В рассматриваемой многокорпусной установке почти полностью исключено самоиспарение раствора в выпарных аппаратах, что приводит к выравниванию тепловых нагрузок по корпусам установки.

1 ‒ термокомпрессор; 2 ‒ выпарной аппарат;

3 ‒ подогреватель исходного раствора

I ‒ исходный раствор; II ‒ упаренный раствор;

III ‒ конденсат; IV ‒ вторичный пар

Рисунок 25.1 ‒ Схема одного корпуса многокорпусной

выпарной установки с тепловым насосом

Затраты на реализацию процесса выпаривания в рассматриваемой многокорпусной установке связаны с работой регенеративных подогревателей

, (25.5)

где n ‒ число корпусов выпарной установки; Т₁ ‒ температура процесса в первом корпусе; З_П ‒ затраты на содержание регенеративного подогревателя; П ‒ регенеративный подогреватель.

Полученное выражение принимает минимальное значение при полезной разности температур в регенеративном подогревателе

. (25.6)

Для определения оптимальной температуры процесса в первом корпусе выпарной установки необходимо сначала составить выражение для определения затрат в этом корпусе аналогично выражению (25.3) с добавлением слагаемых, относящихся к регенеративному подогревателю исходного раствора. После чего приравнять к нулю ее первую производную. В результате получим

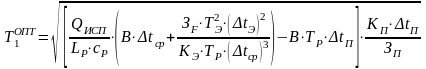. (25.7)

Соотношения (25.4), (25.6), (25.7) позволяют определить оптимальные технологические параметры выпарной установки, зная которые можно найти соответствующее оптимальное число корпусов. Для этого необходимо составить балансовое уравнение, определяющее расход первичного пара. При этом следует учесть, что тепло первичного пара расходуется на дегидратацию раствора постепенно, от корпуса к корпусу, а большая его часть вместе с основным тепловым потоком затрачивается на выпаривание. Фактический расход эксергии первичного теплового потока на компенсацию тепла дегидратации равен

, (25.8)

где 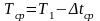‒ средняя температура процесса в выпарной установке.

Эксергетический баланс всей выпарной установки выглядит следующим образом

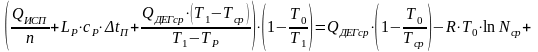
. (25.9)

Исходя из эксергетического баланса, можно определить число корпусов, при котором процесс выпаривания протекает в оптимальном технологическом режиме

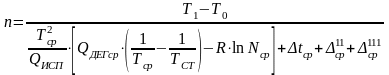. (25.10)

Учитывая, что первое слагаемое в знаменателе является средней физико-химической температурной депрессией, уравнение (25.10) можно записать в более простой форме

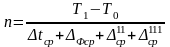. (25.11)

При любых условиях работы многокорпусных выпарных установок для оптимизации процесса требуется значительно увеличить параметры первичного греющего пара (давление, температура) и число корпусов установки по сравнению с традиционными решениями.

Повышение параметров первичного греющего пара снижает его расход, равно как снижает и расход топлива в котельной или ТЭЦ, снабжающих выпарную установку паром. Кроме того, это улучшает параметры выходящих из выпарных аппаратов вторичных паров, что позволяет полнее использовать их эксергетический потенциал как внутри установки, так и за ее пределами. В этом случае появляется возможность реализовать работу установки под противодавлением и получить за счет этого дополнительный экономический эффект. Также при этом уменьшается и общая металлоемкость выпарной установки, так как снижается необходимая поверхность теплообмена. Таким образом, давление первичного греющего пара является регулирующем параметром при оптимизации работы выпарных установок.

Оптимальные полезные разности температур зависят от принятых при проектировании поверхностей теплообмена, которые не меняются в процессе эксплуатации. Поэтому указанные параметры не являются регулирующими при оптимизации работы выпарных установок.

При неизменной поверхности теплообмена выпарной установки с увеличением температуры выпаривания снижаются средняя полезная разность температур и расход эксергии в установке. При неизменной средней полезной разности температур затраты эксергии в процессе теплообмена снижаются пропорционально квадрату абсолютной температуры процесса согласно уравнению (25.2) и не зависят от числа корпусов установки. От числа корпусов не зависят также потери эксергии, связанные с компенсацией гидростатической и гидродинамической температурных депрессий при постоянстве их среднего значения. Эти температурные депрессии уменьшаются с ростом температуры первичного греющего пара, в результате чего значительно сокращаются потери эксергии в установке, связанные с преодолением этих депрессий.

Параграф 26. Рекуперация тепла в сложных ЭХТС. Метод Линхофа.

В любом технологическом процессе высокопотенциальное тепло неизбежно превращается в низкопотенциальное, которое сосредотачивается преимущественно во ВЭР. Таким образом низкопотенциальное тепло всегда имеется в избытке, и приходится искать способы его рационального использования. Однако проблема состоит не просто в экономии энергии, а в сохранении ее качества.

Общие принципы рекуперации тепла (возврата его части для повторного использования в том же технологическом процессе) вытекают из второго закона термодинамики и заключаются в необходимости уменьшения движущих сил во всех точках теплообменников. Однако реальное осуществление этих принципов является сложной задачей, особенно в таких системах, в которых велико число потоков различного потенциала и число вариантов рекуперации энергии.

Одним из действенных приемов, используемых для оценки возможности рекуперации тепловой энергии в сложных ЭХТС, является метод, предложенный Б. Линхофом. Это метод температурного соответствия.

Известно, что при уменьшении движущих сил тепломассообменных процессов не только снижаются эксергетические потери в них, но довольно часто увеличиваются капитальные затраты, связанные с изготовлением аппаратов с большей поверхностью. Тем не менее, возможны и такие варианты реализации теплообменных процессов, при которых одновременно уменьшаются как энергетические, так и капитальные затраты, связанные с аппаратурным оформлением этих процессов. Простейшим примером, иллюстрирующим такую возможность, может служить схема теплообмена трех материальных потоков (рисунок 26.1, а). В рассматриваемом процессе три потока нагреваются от 350 до 450 К паром с температурой 530 К. Одновременно с этим три потока с температурой 600 К охлаждаются до 500 К водой с температурой 300÷310 К. Требуемый результат в рассматриваемом случае можно получить без расхода пара и воды (рисунок 26.1, б).

Рисунок 26.1 ‒ Схемы нагревания и охлаждения технологических потоков

с использованием пара и воды (а) и без их использования (б)

Суть метода Линхофа заключается в следующим. Строят график, характеризующий величину и направление тепловых потоков в анализируемой системе во всех характерных температурных интервалах и анализируют его с целью нахождения участков с самокомпенсирующимися тепловыми потоками. На рисунке 26.2 в координатах температура-энтальпия построены такие графики для системы с тремя материальными потоками. Прямая I соответствует процессу охлаждения потока с начальной температурой 550 К, а прямые II и III ‒ процессу нагревания потоков с начальными температурами 350 и 450 К соответственно. Данная диаграмма является основой для построения общего графика, характеризующего отведение или подведение в системе тепла в каждом интервале изменений температур потоков. Этот график представлен в правой части рисунка 26.2. Его анализ и позволяет выявить возможность экономии тепла в рассматриваемой системе.

Рисунок 26.2 ‒ Диаграмма Линхофа

В данном случае некоторые прямые имеют положительный угол наклона к оси абсцисс. К ним относятся линии DВ и GF, которые соответствуют процессам нагревания. Соответственно линии АВ, DF и GH характеризуют температуру и количество тепла, которое необходимо отвести из системы. Из графика видно, что потребность в тепле на участке DB частично можно покрыть за счет тепла, отводимого с участка АВ (отрезок CB). Этого тепла, имеющего температуру выше, чем температура теплового потока на линии DB, достаточно для удовлетворения потребностей системы в тепле на этом участке. Аналогично, за счет тепла, выделяющегося на участке EF, можно покрыть потребность в тепле на линии GF. Все остальные тепловые потоки в системе невозможно подвести и отвести за счет рекуперации внутреннего тепла. Для этого на линии DC необходимо подводить тепло извне, а также отводить его из системы для ее охлаждения на линиях DE и GH. Тепловые потоки на этих участках соответствуют минимуму тепловых затрат, к которому следует стремиться при проектировании системы (в точках В и F разности температур равны нулю).

Преимуществом метода Линхофа является то, что вид графиков не зависит от схемы рекуперации тепла. Для его применения необходимо знать лишь параметры участвующих в процессе тепловых потоков, позволяющие построить график, характеризующий изменение суммарной тепловой нагрузки во всех температурных интервалах. На графике обязательно есть точка, соответствующая минимуму энтальпии (на рисунке 26.2 это точка D), выше которой требуется подвод, а ниже ‒ отвод тепла. Эта точка получила название «узкое место» или «бутылочное горло». Иначе говоря, это означает, что в любой схеме всегда не хватает высокопотенциального тепла и имеется излишек низкопотенциального тепла. Таким образом, в рассматриваемом случае нецелесообразно передавать тепло с уровня выше 450 К на более низкий уровень, так как при этом потребуется дополнительный подвод тепла извне для компенсации его потерь. Поэтому, если в ходе анализа схемы обнаруживается, что в ней нарушен «запрет перехода через «бутылочное горло», она должна быть заменена на другую, в которой нет такой потери теплового потенциала. В любом случае рекуперацию тепла следует проводить между потоками с близкими температурами.

Существует вариант метода Линхофа, в котором строят не единый суммарный график нагревания и охлаждения, а раздельно общие графики нагревания и охлаждения (рисунок 26.3). При анализе конкретных схем теплообмена с помощью таких графиков в первую очередь необходимо обнаружить и устранить перенос тепла с верхнего уровня вниз через «бутылочное горлышко» (ΔТ_min). Далее следует стремиться устранить «диагональный» перенос вблизи «бутылочного горлышка» и, наконец, устранить «диагональные» переносы,