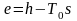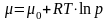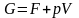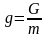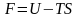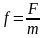- •1 ‒ Анализируемый объект; 2, 3 ‒ соответственно источники и приемники
- •1 ‒ Вентилятор; 2 ‒ теплообменник (калорифер); 3 ‒ сушильная камера
- •1 ‒ Теплообменник; 2 ‒ сушильная камера; 3 ‒ пылеуловитель;
- •4 ‒ Конденсатор; 5 ‒ каплеуловитель; 6 ‒ вентилятор
- •1, 2 ‒ Начальное и конечное состояния горячего теплоносителя;
- •3, 4 ‒ Начальное и конечное состояния холодного теплоносителя
- •I, II ‒ охлаждаемые потоки; III, IV ‒ нагреваемые потоки
- •1 ‒ Штуцер для перегретого пара; 2 ‒ винтовая насадка; 3 ‒ форсунки;
- •4 ‒ Штуцер для насыщенного пара; 5 ‒ патрубок для отвода воды
- •1 ‒ Компрессор; 2 ‒ конденсатор; 3 ‒ дроссель; 4 ‒ испаритель
- •1 ‒ Компрессор; 2 ‒ подогреватель; 3 ‒ сушильная камера;
- •4 ‒ Теплообменник; 5 ‒ сепаратор; 6 ‒ испаритель;
- •7 ‒ Дроссельное устройство; 8 ‒ нагреватель-конденсатор
- •I ‒ экзотермическая реакция; II ‒ эндотермическая реакция;
- •III ‒ вспомогательная реакция
- •Список использованной литературы
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
(ФГБОУ ВПО)
Волгоградский государственный технический университет
(ВолгГТУ)
Кафедра «Процессы и аппараты химических производства»
(«ПАХП»)
Курс лекций по дисциплине
«Теоретические основы энерго- и ресурсосбережения
в химических производствах»
(«ТОЭРС»)
Разработал:
Васильев Пётр Сергеевич
2013
Параграф 1. Классификации основных видов энергии и ресурсов.
Химическая промышленность ‒ одна из самых энергоемких. Во многих химических производствах расходные коэффициенты сырья достигают 3÷4 т на 1 т продукта, а в некоторых случаях превосходят 5÷6 т.
В производстве химических продуктов различают исходные вещества (сырье), промежуточные продукты (полупродукты) и готовые продукты.
Сырье химической промышленности классифицируют по различным признакам:
по происхождению: минеральное, растительное и животное;
по запасам: невозобновляемое (руды, минералы, горючие ископаемые) и возобновляемые (вода, воздух, растительное и животное сырье);
по химическому составу: неорганическое (руды, минералы) и органическое (нефть, уголь, природный газ);
по агрегатному состоянию: твердое (руды, минералы, уголь, сланцы, торф), жидкое (вода, рассолы, нефть) и газообразное (воздух, природный газ).
Кроме того, сырье можно подразделить на первичное (минеральное, растительное и животное, горючие ископаемые, вода и воздух) и искусственное (кокс, химические волокна, синтетический каучук, смолы).
В свою очередь минеральное сырье включает рудное (руды металлов), нерудное (поваренная соль, гипс, фосфориты, апатиты, глина, известняк, песок) и горючее (торф, бурые и каменные угли, сланцы, природный газ).
С позиции энергосбережения сырье, применяемое в химико-технологических процессах (ХТП), должно обеспечивать:
минимальное число стадий переработки в конечный продукт;
минимальные энергетические и материальные затраты на осуществление ХТП;
минимальное рассеяние исходной энергии, т. е. характеризоваться максимумом эксергии;
возможно более низкий уровень температуры, давления, расхода энергии на изменение агрегатного состояния веществ участников ХТП;
максимальную концентрацию целевых продуктов в реакционной смеси.
В настоящее время известно пятнадцать видов энергии, из которых практическое значение пока имеют девять:
ядерная ‒ энергия связи нейтронов и протонов в ядре, освобождающаяся в различных видах при делении тяжелых и синтезе легких ядер; в последнем случае ее называют термоядерной;
химическая (атомная) ‒ энергия системы из двух или более реагирующих между собой веществ, которая высвобождается в результате перестройки электронных оболочек атомов и молекул при химических реакциях;
электростатическая ‒ потенциальная энергия взаимодействия электрических зарядов, то есть запас энергии электрически заряженного тела, накапливаемый в процессе преодоления им сил электрического поля;
магнитостатическая ‒ потенциальная энергия взаимодействия «магнитных зарядов», или запас энергии, накапливаемый телом, способным преодолеть силы магнитного поля в процессе перемещения против направления действия этих сил;
упругостная ‒ потенциальная энергия механически упруго-измененного тела (сжатая пружина, газ), освобождающаяся при снятии нагрузки чаще всего в виде механической энергии;
тепловая ‒ часть энергии теплового движения частиц тел, которая освобождается при наличии разности температур между данным телом и телами окружающей среды;
механическая ‒ кинетическая энергия свободно движущихся тел и отдельных частиц;
электрическая (электродинамическая) ‒ энергия электрического тока во всех его формах;
электромагнитная (фотонная) ‒ энергия движения фотонов электромагнитного поля.
Часто в особый вид энергии выделяют биологическую. Биологические процессы ‒ это особая группа физико-химических процессов, в которых участвуют те же виды энергии, что и в других.
Непосредственно используются только 4 вида: тепловая (70÷75%), механическая (20÷22%), электрическая (3÷5%) и электромагнитная (1%). Главным источником используемых видов энергии является химическая энергия минеральных органических горючих.
Все виды энергии можно разделить на три группы.
Первичная энергия Э1 ‒ химическая энергия ископаемого первичного топлива с учетом энергетических затрат на добычу, подготовку (обогащение), транспортировку и т. д..
Производная энергия Э2 ‒ энергия преобразованных энергоносителей, например пара, горячей воды, электроэнергии, сжатого воздуха, кислорода, воды и других, с учетом затрат на их преобразование.
Скрытая энергия Э3 ‒ энергия, затраченная на подготовку исходного сырья, на изготовление технологического, энергетического и другого оборудования, капитальных сооружений, инструмента и т. д.. К этой же форме энергии относятся энергозатраты по поддержанию оборудования в работоспособном состоянии (ремонты), энергозатраты внутризаводских и межзаводских перевозок и других вспомогательных операций. Для многих массовых видов продукции величина энергетических затрат в виде скрытой энергии является относительно незначительной по сравнению с другими двумя видами энергии, и поэтому в первом приближении может включаться в расчет по примерной оценке.
Полные энергозатраты на производство единицы какой-либо продукции в этом случае можно записать в виде
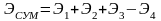 ,
(1.1)
,
(1.1)
где Э4 ‒ энергия вторичных энергетических ресурсов.
Суммарные энергозатраты называют также технологическим топливным числом (ТТЧ) конкретного вида продукции (бензина, кирпича и др.).
Топливно-энергетические ресурсы (ТЭР) ‒ это часть природных ресурсов, скопления минералов в недрах земной коры в промышленных концентрациях. Рациональность их использования определяется полнотой отбора, степенью использования, удельными затратами на производство конечного продукта, окупаемостью использования данного вида полезного ископаемого, степенью сохранения окружающей среды и другими показателями, определяющими политику энергосбережения.
Существенным источником химического сырья являются вторичные материальные ресурсы (ВМР). К ним относятся отходы производства (остатки сырья, материалов и продуктов, образующиеся в процессе производства продукции, которые частично или полностью утратили свои качества и не соответствуют стандартам или ТУ), отходы потребления (различные бывшие в употреблении изделия и вещества, восстановление которых экономически нецелесообразно) и побочные продукты (вещества, образующиеся в процессе переработки сырья наряду с основными продуктами производства, но не являющиеся целью производственного процесса). Те побочные продукты, которые получаются при добычи или обогащении основного сырья, принято называть попутными продуктами (например, попутный газ). За счет использования ВМР экономия сырья и материалов составляет не менее 20÷25% от общего потребления.
Вторичными энергетическими ресурсами (ВЭР) называется энергетический потенциал продукции, отходов, побочных и промежуточных продуктов, образующихся в технологических агрегатах, который не используется в самом агрегате, но может быть частично или полностью использован для энергоснабжения других агрегатов. По виду энергии ВЭР разделяют на три группы:
горючие (топливные): химическая энергия отходов технологических процессов химической и термохимической переработки углеродистого или углеводородного сырья, побочных горючих газов плавильных печей и т. д.;
тепловые: физическая теплота отходящих газов технологических агрегатов основной, побочной, промежуточной продукции и отходов основного производства, рабочих тел систем принудительного охлаждения технологических агрегатов и установок, горячей воды и пара, отработанных в технологических и силовых установках, а также теплота экзотермических реакций;
избыточного давления: потенциальная энергия газов и жидкостей, выходящих из технологических агрегатах с избыточным давлением.
Параграф 2. Тепловая энергия и ее использование на химических предприятиях.
Все виды энергии, которые используются человеком, можно разделить на две группы:
упорядоченную энергию (механическую, электрическую и электромагнитную), которая может трансформироваться в другие виды энергии и передаваться при любых внешних условиях, а потенциал ее всегда остается высоким;
хаотичную, неупорядоченную энергию (тепловую), которая может передаваться от тела к телу только при определенных внешних условиях, так как для произвольной передачи тепла обязано соблюдаться условие неравенства температур тела, отдающего тепло, и тела, тепло воспринимающего.
Доля потребления тепловой энергии составляет 70÷75% от общего энергопотребления любого химического предприятия, которое получает ее либо от расположенной поблизости тепловой электрической станции (ТЭС), например от теплоэлектроцентрали (ТЭЦ), либо от ТЭЦ, имеющейся в структуре самого химического предприятия. Основным источником тепловой энергии служит топливо, главными технологическими характеристиками которого являются теплота сгорания и жаропроизводительность.
Теплота сгорания (теплотворная способность) ‒ это теплота реакции горения топлива, т. е. количество теплоты, которое выделяется при полном сгорании 1 кг твердого или жидкого топлива (кДж/кг) или 1 м3 газообразного топлива (кДж/м3) и при охлаждении продуктов горения до начальной температуры процесса. Различают низшую QН (количество теплоты, выделяющееся при сгорании 1 кг водорода с образованием водяного пара) и высшую QВ (количество теплоты, выделяющееся при сгорании 1 кг водорода с образованием воды) теплоту сгорания топлива. В практических расчетах обычно пользуются величиной QН.
Жаропроизводительность ‒ максимальная температура горения, развиваемая при полном сгорании топлива без избытка воздуха, в условиях, когда вся выделяющаяся при сгорании теплота полностью расходуется на нагрев образующихся продуктов сгорания. Жаропроизводительность топлива Tmax прямо пропорциональна его теплоте сгорания и обратно пропорциональна расходу теплоты на нагрев продуктов сгорания до температуры Tmax.
Жаропроизводительность положена в основу энергетической классификации топлива. В зависимости от жаропроизводительности топливо подразделяют на две группы: высокой (Tmax>2300 К) и пониженной (Tmax<2300 К) жаропроизводительности.
Потребителей тепловой энергии можно разделить на следующие группы:
технологические (в среднем 77% от общегодового потребления);
отопительно-вентиляционные (18%);
хозяйственно-бытовое горячее водоснабжение (5%).
Технологические потребители ‒ это различные тепло- и массообменные устройства, реакторы, другие аппараты, в основном поверхностного типа, служащие для нагрева или охлаждения промежуточных теплоносителей, рабочих тел и т. д. Они отличаются очень большим разнообразием функционального назначения и конструктивного исполнения, что прямо связано с большим многообразием сред, подвергаемых тепловой обработке, и их физико-химических свойств.
В зависимости от температурного уровня технологических процессов в качестве первичных энергоресурсов используются следующие.
Органическое топливо (твердое, жидкое, газообразное), которое при сжигании дает высокотемпературный теплоноситель ‒ продукты сгорания (дымовые газы), температура которых может достигать 1800÷2000 °С и выше. Топливо чаще всего используется для тепловой обработки продуктов в печах и для получения пара и горячей воды в котлах. Кроме того, топливо является основным сырьевым продуктом для промышленности органического синтеза и нефтехимии. Здесь для высокотемпературного нагрева технологических потоков используются трубчатые печи, в которых нагреваемый жидкий или газообразный продукт течет в трубах, снаружи обтекаемых продуктами сгорания топлива. В качестве топлива на химических предприятиях может использоваться не только естественное природное топливо, но и побочные продукты технологии (отходы), которые имеют в своем составе горючие элементы (C, H, S и др.).
Сухой насыщенный или слегка перегретый водяной пар давлением 0,2÷1,4 МПа, реже до 8÷9 МПа. Пар поступает на предприятие от ТЭЦ или районной котельной или же может вырабатываться на самом предприятии в котлах-утилизаторах, топливных котлах в технологических установках за счет теплоты экзотермических химических реакций и при охлаждении потоков продуктов и элементов аппаратов и устройств.
Горячая вода применяется обычно при температурах не выше 180 °С, так как при большей температуре вода должна находиться под давлением большим 1,0 МПа, что требует для обеспечения прочности массивных и тяжелых теплообменных устройств. Как и пар, вода может поступать от ТЭЦ или районных котельных, или вырабатываться на самом предприятии.
Холодная вода при температуре окружающей среды или охлажденная в специальных охладителях до температуры 4÷25 °С используется как холодный теплоноситель для отвода теплоты от технологических потоков и устройств.
Воздух также широко используется как охлаждающий теплоноситель. Кроме того, воздух используется как горячий теплоноситель и как сушильный агент.
Холодильные агенты (рассолы, фреоны, аммиак, углекислота и др.) применяются в области температур ниже температуры окружающей среды, в том числе при минусовых температурах. Холодильные агенты и вода обычно циркулируют по замкнутой системе циркуляции между охлаждаемым объектом и охладителем (бассейн, пруд).
Потребление теплоты в технологических процессах характеризуется непрерывностью и определенным постоянством. Основной теплоноситель – пар. Примерно 90% технологических потребителей пара и горячей воды на конечной стадии потребления используют теплоносители с температурой до 150 °С.
Отопительно-вентиляционные системы. Основным теплоносителем являются пар и горячая вода с температурой не выше 150°С. Отопление производственных помещений в основном воздушное, совмещенное с вентиляцией. Такие совмещенные системы несут около 85÷90% отопительно-вентиляционных нагрузок. В приточных системах вентиляции атмосферный воздух, в зависимости от времени года имеющий температуру от -40 до +10 °С, подогревается в калориферах систем до 25÷40 °С за счет теплоты пара или горячей воды. В летнее время, когда температура воздуха высока, его нужно охлаждать в калориферах холодной водой. Для подготовки воздуха, подаваемого в производственные помещения часто используют кондиционеры, которые являются крупными потребителями тепловой энергии на химических предприятиях. Тепловая нагрузка имеет сезонный характер.
Системы хозяйственно-бытового горячего водоснабжения имеют постоянную, круглогодичную нагрузку. Это в основном душевые, мойки, прачечные, столовые. Конечный теплоноситель ‒ горячая вода с температурой 45÷70 °С. Режим потребления горячей воды непрерывный, с резко выраженными кратковременными пиками нагрузок после окончания каждой смены (увеличение в 5÷8 раз по сравнению со среднечасовым потреблением в течении суток).
Состав энергокомплекса химического предприятия. Система энергоснабжения крупного химического предприятия включает в себя ряд подсистем.
К источникам энергии относятся ТЭЦ, ГЭС, АЭС, котельные, машинокомпрессорные, холодильные и воздухоразделительные станции, источники водоснабжения.
Хранилища топлива и преобразователи энергии представлены топливными складами, мазутохранилищами, газгольдерами, бойлерными, газораспределительными станциями, редукционно-охладительными установками (РОУ), компрессорами, электротрансформаторами, установками сушки воздуха, станциями водоподготовки.
К энергокоммуникациям относят электросети, трубопроводы мазута и газа, пара, воздуха, воды, холода.
Энергоносители, подводимые потребителю, включают топливо в котельные или в топки аппаратов и печей, тепловую и электрическую энергию, холод, сжатые газы, воду.
Энергоприемниками технологических установок являются горелки, форсунки, топки, теплообменники, двигатели. Для передачи энергии из энергоприемников в технологические аппараты используют дымоходы и газоходы, воздухопроводы, трубопроводы растворов, расплавов, а также валы, муфты, редукторы.
В качестве промежуточных внутриагрегатных энергоносителей применяют дымовые газы, горячий воздух, органические теплоносители, нагретые растворы и расплавы.
Параграф 3. Определение потребного количества сырья и энергоресурсов.
Любая технологическая установка или аппарат с точки зрения термодинамики представляет собой термодинамическую систему.
Термодинамическая система ‒ это совокупность материальных тел, ограниченных контрольной балансовой поверхностью, находящихся в механическом и тепловом взаимодействии друг с другом и с внешними телами, не входящими в систему ‒ окружающей средой.
Контрольная балансовая поверхность является мысленной поверхностью, отделяющей рассматриваемую термодинамическую систему от окружающей среды. В зависимости от цели анализа этой поверхностью считают весь объект или только его часть. Необходимо также, чтобы эта поверхность не изменялась во время анализа.
В зависимости от характера взаимодействия термодинамической системы с окружающей средой выделяют следующие виды термодинамических систем:
открытые (происходит обмен энергией и веществом);
закрытые (происходит только обмен механической и тепловой энергией);
изолированные (всякий обмен отсутствует).
Для определения потребного количества сырья технологической установки или аппарата используют материальный баланс. Рассмотрим некую обобщенную реальную систему (рисунок 3.1).

1 ‒ Анализируемый объект; 2, 3 ‒ соответственно источники и приемники
потоков вещества (М), тепловых потоков (Q) и работы (L)
Рисунок 3.1 ‒ Схема материальных и энергетических потоков
в реальной системе
Материальный баланс этой системы имеет вид
 ,
(3.1)
,
(3.1)
где
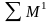 и
и
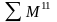 ‒ суммарные материальные потоки,
входящие в объект и выходящие из него;
‒ суммарные материальные потоки,
входящие в объект и выходящие из него;
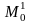 ‒ поток вещества, поступающий из
окружающей среды;
‒ поток вещества, поступающий из
окружающей среды;
 ‒ изменение массы вещества в объекте.
‒ изменение массы вещества в объекте.
Для стационарного
процесса
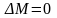 .
Если объединить поток массы из окружающей
среды (он может быть равен и нулю) с
остальными потоками, то материальный
баланс примет вид
.
Если объединить поток массы из окружающей
среды (он может быть равен и нулю) с
остальными потоками, то материальный
баланс примет вид
 .
(3.2)
.
(3.2)
Для процесса, в котором происходит химическое превращение, материальный баланс записывается в виде стехиометрического уравнения.
В технологической линии встречаются различные потоки: последовательные, смешения, разделения, параллельные, возвратные, байпасные.
Процессы разделения представляют наиболее обширную группу. Для них (рисунок 3.2) всегда выполняется соотношение
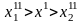 ,
(3.3)
,
(3.3)
где х ‒ мольная доля вещества.

Рисунок 3.2 ‒ Расчетная схема процесса разделения
Будем считать, что поток номер 1 поступает на дальнейшую переработку, а поток 2 – на переработку отходов и рекуперацию сырья. Эффективность аппарата разделения может быть оценена с помощью коэффициента разделения и будет равна
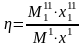 .
(3.4)
.
(3.4)
Коэффициент разделения всегда меньше единицы. Он может характеризоваться как некоторый коэффициент полезного действия процесса и оборудования, характеризующий степень использования сырья. Коэффициент эффективности использования материальных ресурсов для оборудования, через которые материальные потоки проходят транзитом (теплообменники и другие), можно принять равным единице. Это оборудование, в котором поток перерабатываемых веществ поступает через один патрубок и выводится только через один патрубок.
В таблице 3.1 приводятся средние статистические значения коэффициентов полезного действия для различных процессов разделения химической технологии.
Таблица 3.1 ‒ Значения коэффициентов эффективности использования сырья для ряда процессов разделения химической технологии
Процесс |
Значение коэффициента |
1 |
2 |
Отстаивание (гравитационное) |
0,95÷0,98 |
Отстаивание (центробежное) |
0,98 |
Фильтрование (центробежное) |
0,9÷0,98 |
Сушка |
0,9÷0,99 |
Ректификация, перегонка |
0,85÷0,95 |
Абсорбция |
|
Размол, дробление, классификация |
0,99 |
Упаковка, фасовка |
0,995 |
Основой расчета потребного количества энергоресурсов являются уравнения теплового баланса по каждой стадии технологической схемы (рисунок 3.1).
Тепловой баланс имеет вид
 ,
(3.5)
,
(3.5)
где Q1 и Q11 ‒ потоки тепла, входящие в объект и выходящие из него; L1 и L11 ‒ работа, подводимая к объекту и получаемая от него; Q0 ‒ тепло, отдаваемое в окружающую среду или получаемое от нее.
Если объект обменивается с другими объектами энергией только в форме тепла, то соответствующий тепловой баланс имеет вид
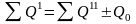 .
(3.6)
.
(3.6)
Приведенные уравнения позволяют определить минимально необходимое количество тепловой энергии, требуемого для реализации технологии. По этим уравнениям рассчитывают количество энергии, которое необходимо передать перерабатываемым веществам или отвести от них, при выполнении соответствующей тепловой операции.
Тепловые потери, которые сопровождают любой процесс передачи тепла, обычно регламентируются в пределах 3÷5% от полезного количества тепла, необходимого для реализации процесса.
Параграф 4. Причины потерь материальных и энергетических ресурсов в технологическом оборудовании. Основные направления использования ВЭР.
Правила эксплуатации оборудования (по пожаро- и взрывоопасности и токсичности) не допускают возможностей утечки материальных потоков в окружающее пространство в условиях штатного функционирования. С этой точки зрения оборудование можно считать системами закрытыми. С термодинамической точки зрения же технологическое оборудование не является закрытой системой. В любом оборудовании осуществляется обмен тепловыми потоками с окружающей средой, который приводит к значительному рассеянию тепловой энергии в окружающую среду.
Передача тепловой энергии возможна при наличии разности температур между телом, тепло отдающим, и телом, воспринимающим тепло. Это означает, что тело, воспринимающее тепло, не может быть нагрето до начальной температуры тела, отдающего тепло. Передача тепла всегда сопровождается снижением температуры теплоносителя. В технологическом оборудовании происходит образование вторичных тепловых потоков с температурным потенциалом ниже, чем у первичных.
В оборудовании разделения происходит образование двух материальных и тепловых потоков. Один из этих тепловых потоков содержит целевой компонент и поступает на переработку в следующее по технологической схеме оборудование. Второй поток, содержащий незначительное количество целевого компонента и тепловой энергии, в большинстве случаев попадает в отходы. В редких случаях осуществляется извлечения остатков целевого вещества из этого потока, и практически никогда не используется тепловая энергия, содержащаяся в этом потоке. В процессах разделения неизбежно попадание части целевого вещества в поток, который далее попадает в отходы, и в редких случаях – в схему рекуперации. Схемы рекуперации, как правило, содержат в своем составе целый ряд процессов разделения. Поэтому любая схема регенерации не позволяет извлечь целевое вещество полностью. Таким образом, за счет этого неизбежны потери перерабатываемых веществ.
Потери материальных и энергетических ресурсов связаны, в значительной степени, с несовершенством используемых в промышленной практике процессов и оборудования. Скорость процессов зависит от величины движущей силы (разности температур или концентрации вещества, концентрации вещества и т. д.). По мере завершения процесса движущая сила его уменьшается, и скорость процесса снижается. В этих условиях эффективность использования оборудования падает. Целесообразность осуществления процессов с экономической точки зрения становится нежелательной. Поэтому ни один из промышленных процессов не проводят до падения движущей силы до нуля. Как следствие, это приводит к неполному использованию сырья.
В таблице 4.1 приведены основные причины, приводящие к потерям тепловых и материальных ресурсов. Как видно из таблицы, причины потерь материальных и энергетических ресурсов в значительной степени совпадают.
Таблица 4.1 ‒ Причины потерь в технологическом оборудовании
Причины потерь |
Потоки |
|
материальные |
тепловые |
|
1 |
2 |
3 |
Снижение движущей силы |
+ |
+ |
Обмен с окружающей средой |
‒ |
+ |
С потоками разделения |
+ |
+ |
Снижение потенциала |
+ |
+ |
Несовершенство оборудования |
+ |
+ |
С вторичными энергоресурсами |
+ |
+ |
В таблице 4.2 приведены сводные данные по использованию водных ресурсов в различных отраслях промышленности, хорошо отражающие неполноту использования (нерациональное использование) ресурсов из-за несовершенства технологического оборудования.
Таблица 4.2 ‒ Структура водопотребления в отраслях промышленности
Отрасль промышленности |
Объем водопотреб-ления |
Объем воды на охлаждение (от объема водопотребления) |
Объем оборотной воды (от объема водопотребления) |
|
км3/год |
км3/год |
км3/год |
1 |
2 |
3 |
4 |
Теплоэнергетика |
150 |
144 |
86,4 |
Черная металлургия |
36 |
27 |
21,6 |
Цветная металлургия |
10 |
2 |
1,6 |
Химия |
9 |
6,7 |
5 |
Нефтехимия и нефтепереработка |
18 |
17,1 |
15,2 |
Целлюлозно-бумажная промышленность |
3,4 |
0,24 |
0,16 |
Ресурсосбережение ‒ система мер по обеспечению рационального использования ресурсов, удовлетворению прироста потребности в них народного хозяйства, главным образом за счет экономии.
Так как характерной особенностью многих химических производств является наличие значительных тепловых «отходов», то повышение энергетической эффективности таких производств не может быть достигнуто без рационального использования ВЭР.
В зависимости от видов и параметров рабочих тел различают четыре основных направления использования ВЭР:
топливное: непосредственное использование горючих компонентов в качестве топлива;
тепловое: использование теплоты, получаемой непосредственно в качестве ВЭР или теплоты и холода, вырабатываемых за счет ВЭР в утилизационных установках, а также абсорбционных холодильных установках;
силовое: использование механической или электрической энергии, вырабатываемой в утилизационных установках за счет ВЭР;
комбинированное: использование теплоты, электрической или механической энергии, одновременно вырабатываемых за счет ВЭР.
ХТС, в которых реализуется комбинированный метод, называют энергохимико-технологическими системами (ЭХТС), позволяющие приблизиться к созданию безотходных технологий как по материалам, так и по энергии. В ЭХТС энергетическое оборудование органически связано с химико-технологическим в единый комплекс, в котором всякому изменению параметров химических процессов должны сопутствовать изменения параметров энергетического оборудования и наоборот. Таким образом, в ЭХТС имеет место такое сочетание технологического и энергетического оборудования, при котором их раздельная работа оказывается невозможной. В этих условиях задача оптимизации ЭХТС сводится к отысканию наиболее эффективного сочетания характеристик и режимов работы химического и энергетического оборудования, обеспечивающих уменьшение затрат топливно-энергетических ресурсов при высоких технологических показателях с учетом капитальных затрат (оптимальный выход продукта, максимальная степень использования сырья и т. д.).
Техническим воплощением подобной оптимизации могут являться способ замкнутого водоснабжения, обеспечение и повышение надежности и рациональная компоновка оборудования химических производств и т. д..
Таким образом, с математической точки зрения, большая часть задач ресурсосбережения является задачами оптимизации, целью которых является нахождение экстремума целевой функции. При этом в целевую функцию должен входить один или несколько критериев, влияющих на протекаемый в ЭХТС процесс. А величина этих критериев должна быть напрямую связана с расходом ресурсов в ЭХТС.
Основным этапом оптимизации ЭХТС является проведение ее термодинамического анализа.
Параграф 5. Термодинамический анализ ХТС: предмет, цели и алгоритм проведения. Термодинамические функции состояния.
При анализе степени совершенства ХТС последовательно рассматриваются материальный, энергетический и эксергетический балансы. Предметом термодинамического анализа является изучение энергетического и эксергетического балансов, а также факторов, влияющих на их составляющие.
Методы термодинамического анализ применимы к любой ХТС, поскольку в них происходит преобразование вещества, а следовательно и преобразование энергии.
Термодинамический анализ преследует следующие основные цели:
учет степени термодинамического совершенства протекающих процессов в ХТС и ее элементах;
отыскание путей экономии исходных продуктов, топлива и электроэнергии;
повышение полноты использования продуктов, а также разного рода теплоносителей, вводимых в ХТС и ее отдельные элементы.
Термодинамический анализ должен дать ответ на четыре главных вопроса:
каким был бы эффект функционирования системы при идеальном, т. е. обратимом течении процессов;
насколько велико отличие реального эффекта от идеального;
как распределяются потери по отдельным элементам установки;
на совершенствование работы какой части установки требуется прежде всего обратить внимание.
Термодинамический анализ ХТС целесообразно проводить на всех стадиях подготовки системы к эксплуатации, а именно на предпроектной, проектной, конструктивной и эксплуатационной. Существуют оценки, по которым примерно 40% потерь зависят от выбора схемы технологического процесса при его эскизной проработке. Еще 40% определяются проектным решением. Таким образом, примерно на 80% потерь в ходе эксплуатации воздействовать уже невозможно. Поэтому термодинамический анализ имеет особенно важное значение на стадиях эскизной компоновки и проектирования.
При проведении термодинамического анализа с целью оптимизации системы рекомендуется придерживаться следующего алгоритма.
Проверить, необходимо ли предусмотренное количество исходного продукта и нет ли в распоряжении другого, более выгодного сырья или источника первичной энергии.
Рассмотреть целесообразность применения принципа многоступенчатости. Известно, что использование больших разностей движущих сил (давлений, температур и т. д.) приводит к большим потерям из-за возрастания необратимости процессов. Если же разделить полный перепад движущих сил на малые ступени, то эти потери во многих случаях можно значительно снизить. Однако при этом увеличатся затраты на более сложную многоступенчатую установку. Этот принцип находит применение в многоступенчатых компрессорах, систем теплообменников, цепей реакторов, каскадных схемах и т. д.
Рассмотреть возможность использования принципа регенерации, т. е. создания обратных потоков вещества и энергии с целью их утилизации. За счет этого, как правило, улучшаются экологические показатели ХТС, что обычно сопровождается и уменьшением внешних потерь, а также увеличивается эффективно срабатываемый в системе перепад движущих сил. Данный принцип используется, например, для создания обратного потока непрореагировавшего компонента при осуществлении химической реакции, а также в регенеративном теплообмене, который представляет собой одно из наиболее эффективных средств повышения экономичности процессов.
Рассмотреть возможность интеграции, состоящей в объединении различных функций в одной технической системе. Современные ЭХТС являются ярким примером реализации этого принципа. Интегрирование приводит к заметным энергетическим эффектам, так как значительно сокращается протяженность коммуникаций, уменьшается площадь внешних теплоотдающих поверхностей, обеспечивается комплексное использование сырья.
Рассмотреть возможность снижения потерь за счет использования уходящих из системы потоков вещества и энергии. Такое использование можно проводить двумя путями. Так называемое первичное использование означает возвращение вещества или энергии в исходную систему и поэтому тесно связано с эффектом регенерации. Вторичное использование означает применение вещества или энергии вне системы и приводит к объединению или комбинированию различных систем.
В современной практике находят применение три метода термодинамического анализа: энергетический, энтропийный, эксергетический (таблица 5.1). Последние два метода близки друг к другу. В обоих случаях изучаются эксергетические потоки и потери эксергии.
В анализе эффективности энергопотребления используются термодинамические функции и взаимосвязь между ними. Эти соотношения приведены в таблице 5.2, в которой m ‒ масса вещества, а удельная изобарная теплоемкость вещества равна
 ,
(5.2)
,
(5.2)
где R ‒ универсальная газовая постоянная.
Таблица 5.1 ‒ Основные методы анализа эффективности использования энергии
Метод анализа |
Основа метода |
Получаемый ответ |
1 |
2 |
3 |
Энергетический |
Первый закон термодинамики. Закон сохранения энергии. |
Сколько энергии необходимо для осуществления процесса (сколько энергии надо передать от одного тела к другому), частично оценить эффективность использования энергии. |
Энтропийный |
Второй закон термодинамики. Условие самопроизвольной передачи теплоты. |
Почему реальный объект отличается от идеального, оценить эффективность использования энергии, как устранить потери энергии. |
Эксергетический |
Второй закон термодинамики. Условие самопроизвольной передачи теплоты. |
Почему при реализации процесса происходит падение работоспособности энергетических потоков и как уменьшить это падение. |
Химический потенциал при нормальных условиях
 ,
(5.1)
,
(5.1)
где Т ‒ температура; р ‒ давление; V ‒ объем.
Таблица 5.2 ‒ Уравнения для расчета термодинамических функций
Название и обозначение |
Взаимосвязь между функциями |
Единицы измерения |
Удельная величина |
Единицы измерения |
1 |
2 |
3 |
4 |
5 |
Внутренняя энергия |
|
Дж |
|
|
Энтальпия |
|
Дж |
|
|
Энтропия |
|
Дж/°С |
|
|
Теплота |
|
Дж |
|
|
Механическая работа |
|
Дж |
|
|
Продолжение таблицы 5.2
Эксергия |
|
Дж |
|
|
Химический потенциал |
- |
Дж |
|
|
Изобарно-изотермический потенциал |
|
Дж |
|
|
Свободная энергия |
|
Дж |
|
|
Если термодинамическая функция в любом процессе в любой термодинамической системе определяется только начальным и конечным состоянием системы и не зависит от характера процесса, то она называется функцией состояния этой термодинамической системы или термодинамическим потенциалом.
В таблице 5.2 такими функциями состояния являются:
внутренняя энергия U ‒ энергия поступательного, вращательного и колебательного молекулярного и внутримолекулярного движений, а также потенциальная энергия сил взаимодействия между молекулами;
энтальпия Н ‒ энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении;
энтропия S ‒ мера необратимости термодинамической системы;
химический потенциал
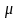 ‒ величина, показывающая изменение
внутренней энергии термодинамической
системы при добавлении в нее одной
частицы, когда сама система при этом
не получала тепла и не совершала работу;
‒ величина, показывающая изменение
внутренней энергии термодинамической
системы при добавлении в нее одной
частицы, когда сама система при этом
не получала тепла и не совершала работу;изобарно-изотермический потенциал (энергия Гиббса) G ‒ величина, показывающая изменение энергии термодинамической системы в ходе химической реакции (полная химическая энергия термодинамической системы);
свободная энергия (энергия Гельмгольца) F ‒ величина, убыль которой в равновесном изотермическом процессе равна работе, совершенной термодинамической системой над внешними телами;
эксергия будет являться функцией состояния термодинамической системы только при заданных значениях температуры T0 и давления p0 в окружающей среде.
Параграф 6. Содержание первого и второго законов термодинамики. Понятие о компенсации.
Первый закон термодинамики является частной формой закона сохранения энергии
 ,
(6.1)
,
(6.1)
где dQ ‒ теплота, подведенная или отведенная от системы; dL ‒ работа изменения объема; dL0 ‒ располагаемая работа, равная разности между работой расширения газа и работой вытеснения.
Первый закон термодинамики отражает обязательный для любого термодинамического процесса баланс между изменением внутренней энергии системы и энергией, которой система обменивается с окружающей средой. Он позволяет, используя уравнение состояния, находить изменение параметров системы в ходе процессов. Однако он никак не определяет возможного направления этих процессов и условий, при которых они будут протекать в нужном направлении. Утверждения, дающие ответы на последние два вопроса, составляют существо второго закона термодинамики.
Исходя из первого закона, теплота и работа ‒ две равноправные формы передачи энергии, однако опыт показывает, что они являются существенно неравноценными с точки зрения их взаимного преобразования и преобразования в другие виды энергии. Работа может непосредственно пойти на увеличение любого вида энергии, в то время как теплота без предварительного преобразования ее в работу, увеличивает лишь внутреннюю энергию системы.
Процесс преобразования работы в теплоту может протекать при изменении состояния только одного теплополучающего тела (например, нагрев тела вследствие работы против сил трения). При обратном же преобразования процесс не ограничивается охлаждением источника теплоты, а обязательно сопровождается изменением состояния других тел, участвующих в процессе. Такое изменение называют компенсацией. Таким образом, преобразование теплоты в работу без компенсации невозможно. Однако обратное преобразование возможно: затрачиваемую работу можно полностью превратить в эквивалентное количество теплоты.
Компенсация влияет на величину полезного преобразования энергии. Вследствие нее работа всегда меньше подведенной теплоты, и КПД<1. Таким образом, компенсация заключается в том, что часть подведенной тепловой энергии отводится в окружающую среду с температурой меньшей, чем температура ее источника.
Параграф 7. Обратимые и необратимые процессы.
Рассмотрим термодинамическую систему, которая в результате некоторого процесса изменяет свое состояние, а затем возвращается к исходному, пройдя в обратной последовательности через те же промежуточные состояния. В ходе процессов система взаимодействует с окружающей ее средой. Будем считать, что система и ее окружающая среда в совокупности составляют общую изолированную систему.
Если при указанных условиях после завершения прямого и обратного процессов ни в системе, ни в окружающей среде не появляются какие-либо остаточные изменения, то процессы называются обратимыми. В противном случае процессы являются необратимыми.
В реальности все естественные процессы, сопровождающиеся трением, диффузией, теплообменом при конечной разности температур, необратимы, потому что в ходе их часть совершаемой или потенциальной работы превращается в теплоту. Обратное преобразование этой теплоты в работу согласно второму закону термодинамики невозможно без компенсации. Для рассматриваемых прямого и обратного процессов компенсация может заключаться только в дополнительном воздействии со стороны окружающей среды. Таким образом, если саму систему удается вернуть в исходное состояние, то окружающая среда в исходное состояние не возвратится.
Различают внутреннюю и внешнюю необратимость. Под внутренней понимают необратимость, которая связана с неравновесным состоянием системы, т. е. с наличием в системе градиентов давления, температур, концентраций, а также с трением внутри системы при условии, что выделившаяся вследствие него теплота не отводится через границы системы.
Внешняя необратимость наблюдается при передаче энергии через границы системы, например, при теплообмене между системой и окружающей средой при конечной разности температур или трении в подшипниках вала, через который передается механическая работа.
Степень необратимости реальных процессов, протекающих в элементах ХТС, может быть различной. При термодинамическом анализе многие из этих элементов могут приближенно рассматриваться как обратимые.
Для внешней обратимости процесс теплообмена между системой и источником или приемником теплоты в окружающей среде должен протекать при отсутствии разности температур. Часто источник или приемник имеет постоянную температуру. В этих условиях единственным реальным процессом, который может приближаться к обратимому, является внутренне обратимый изотермический, протекающий при температуре, как можно более близкой к температуре источника.
Идеализированное представление реальных необратимых процессов в виде обратимых позволяет использовать для их анализа методы классической термодинамики, а уже на полученные результаты наложить эффекты, обусловленные необратимостью.
В качестве меры степени необратимости реальных процессов может служить величина дополнительного внешнего воздействия, например, работы, которую необходимо затратить для того, чтобы возвратить систему в исходное состояние. Это приводит к уменьшению полезной работы системы. Таким образом, необратимость процессов, протекающих в термодинамической системе, приводит к снижению ее работоспособности. Это снижение тем значительней, чем выше степень необратимости.
Существуют процессы, в которых полезная работа вследствие необратимости обращается в ноль. Такие процессы называют предельно необратимые, например, трение, диффузия, теплообмен при конечной разности температур.
Все реальные процессы, протекающие в изолированной системе, идут в направлении достижения равновесия всех ее частей с преобразованием совершаемой или потенциальной работы в теплоту. В силу необратимости протекающих процессов система сама не может выйти из этого состояния. При этом полезная работа внутри этой изолированной системы совершаться не может. В соответствии с первым законом термодинамики общая энергия изолированной системы не меняется и при полном равновесии всех частей системы не может быть преобразована в работу.
Таким образом, в ходе необратимых процессов, протекающих в изолированной системе, энергия, оставаясь количественно неизменной, ухудшается качественно, а возможность получения за счет нее работы уменьшается.
Параграф 8. Математическое выражение второго закона термодинамики. Энтропия как мера необратимости.
Важнейшим следствием второго закона термодинамики является обоснование существования и свойств такой функции состояния, как энтропия. К понятию энтропии можно прийти различными способами, один из которых основывается на анализе особенностей преобразования теплоты в работу в циклах тепловых двигателей. В соответствии со вторым законом для такого преобразования требуется наличие не только источника, но и приемника теплоты. Если предположить, что температуры источника и приемника постоянны, то единственно возможным циклом, обратимым как внутренне, так и внешне, буде обратимы цикл Карно (рисунок 8.1). Этот цикл состоит из двух внутренне обратимых изотерм с температурами рабочего тела
Т1 = ТИСТ = const и Т1 = ТПР = const (8.1)
соответственно, и двух также внутренне обратимых адиабат. Внешняя обратимость для изотерм обеспечивается соблюдением условия (8.1). Адиабаты из-за отсутствия теплообмена всегда внешне обратимы.

А-В ‒ процесс изотермического расширения рабочего тела;
В-С ‒ процесс адиабатного расширения рабочего тела;
С-D ‒ процесс изотермического сжатия рабочего тела;
D-A ‒ процесс адиабатного сжатия рабочего тела
Рисунок 8.1 ‒ Прямой цикл Карно в координатах p и V
Доля подведенной теплоты, преобразованной в полезную работу в любом прямом обратимом цикле, характеризуется термическим КПД
 ,
(8.2)
,
(8.2)
где Q1 ‒ теплота, отданная источником; Q2 ‒ теплота, переданная приемнику.
Среди всех других циклов цикл Карно имеет наибольший термический КПД, который не зависит от свойств рабочего тела, а определяется только температурами T1 и T2. С учетом этого
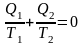 .
(8.3)
.
(8.3)
Любой обратимый цикл, протекающий при переменных T1 и T2, с математической точки зрения можно представить как совокупность бесконечного числа элементарных обратимых циклов Карно. Для любого обратимого цикла имеем
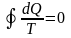 .
(8.4)
.
(8.4)
Интеграл по замкнутому контуру равен нулю, когда подынтегральное выражение есть полный дифференциал некоторой функции. В данном случае подынтегральная функция называется энтропией. Ее изменение в любом элементарном обратимом процессе равно
. (8.5)
При T=const получаем
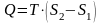 .
(8.6)
.
(8.6)
Предположим, что источник теплоты, ее приемник и обратимая машина Карно образуют в совокупности изолированную систему. Энтропия системы будет оставаться постоянной. Для источника и приемника теплоты изменения энтропии соответственно будут равны
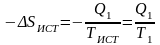 ,
,
 ,
(8.7)
,
(8.7)
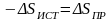 .
.
Согласно (8.4) энтропия рабочего тела за цикл не меняется, поэтому для всей системы изменение энтропии также равно нулю
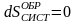 .
(8.8)
.
(8.8)
Предположим теперь, что в той же системе машина Карно работает при TИСТ>T1 и TПР<T2, т. е. имеет место внешняя необратимость, которая приводит к потере работоспособности системы. В результате этого термический КПД необратимого цикла будет меньше, чем у соответствующего ему обратимого
 .
(8.9)
.
(8.9)
При этом
 .
(8.10)
.
(8.10)
Правая часть неравенства представляет собой уменьшение энтропии источника теплоты вследствие отвода от него теплоты Q1, а левая ‒ возрастание энтропии приемника вследствие подвода к нему теплоты Q2. Общая энтропия рассматриваемой изолированной системы в случае необратимого цикла будет возрастать
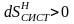 .
(8.11)
.
(8.11)
В итоге математическое выражение второго закона имеет вид
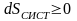 .
(8.12)
.
(8.12)
Таким образом, второй закон термодинамики можно трактовать как закон о существовании энтропии и ее неубывании во всех естественных процессах.
Параграф 9. Понятия эксергии и анергии термодинамической системы. Виды эксергии.
Наиболее рациональным является использование энергии первичных источников с максимально полным извлечением потенциально возможной работы. В связи с этим возникает вопрос об условиях, в которых полученная от системы работа будет максимальна, и об оценке работоспособности системы вследствие необратимости протекающих в ней процессов.
В соответствии с первым законом термодинамики работа, в общем случае, совершается системой за счет ее внутренней энергии, а также в результате преобразования энергии, подведенной от внешних источников в форме теплоты и работы. В соответствии со вторым законом термодинамики теплоту, подведенную к системе, нельзя полностью преобразовать в работу даже при обратимом течении процессов. Это утверждение справедливо и для внутренней энергии системы. Работа за счет внутренней энергии может совершаться до тех пор, пока параметры состояния систем не придут в равновесие с окружающей средой. Оставшийся после достижения равновесия запас внутренней энергии системы не может быть преобразован в работу.
Таким образом, общий энергетический ресурс системы, включающий ее внутреннею энергию и энергию, подводимую извне, всегда может быть разделен на две части: ту, которая при заданных параметрах окружающей среды может быть преобразована в работу, и другую, которая в работу преобразована быть не может.
При обратимом течении процессов первая часть представляет собой максимальную работу, которую может совершить система, и называется эксергией. Вторая часть называется анергией.
В общем случае эксергия E материи является максимальной работой, которую эта материя может совершить в обратимом процессе, с окружающей средой в качестве источника даровых тепла и веществ, если в конце этого процесса все участвующие в нем виды материи приходят в состояние термодинамического равновесия со всеми компонентами окружающей среды. Таким образом, эксергия определяется возможностью взаимодействия рассматриваемой материи с окружающей средой.
В соответствии с первым законом термодинамики сумма энергии для изолированной системы есть величина постоянная:
энергия = эксергия + анергия = const.
Отсюда следует, что уменьшение эксергии изолированной системы приводит к росту анергии, т. е. к увеличенью той части энергии, которая при данных условиях не может быть преобразована в работу.
В частных случаях энергия может целиком состоять из эксергии. Например, электрическая энергия, которая целиком может быть преобразована в работу. С другой стороны, энергия, содержащаяся в окружающей среде, состоит из одной лишь анергии. Энергия, передаваемая в форме теплоты, частично состоит из эксергии и частично из анергии.
В зависимости от вида термодинамической системы и энергии, которая преобразуется в работу, различают
эксергию потока вещества Е (е), которую часто называют просто эксергией;
эксергию вещества в замкнутом объеме Еv (еv);
эксергию потока теплоты Eq (еq);
нулевую химическую эксергию E0 (e0);
эксергию излучения Еε (eε).
Эксергия потока вещества. Пусть на входе в термодинамическую систему поток рабочего тела имеет параметры р1, Т1, Н1, S1. По определению эксергия есть та максимальная работа, которую может совершить поток при обратимом переходе в состояние равновесия с окружающей средой, имеющей параметры р0, Т0, Н0, S0.
Окружающая среда является в данном случае теплоприемником, температура которого постоянна. Поэтому только в изотермическом процессе, протекающим при Т=Т0, возможен обратимый теплообмен между потоком и окружающей средой. Этому процессу должен предшествовать внутренне обратимый адиабатный, который обеспечивает изменение температуры тела от Т1 до Т0. Так как адиабатный процесс протекает без теплообмена с внешней средой, то он всегда внешне обратим.
Таким образом, полностью обратимый переход возможен только при последовательном протекании двух процессов: адиабатного 1-2 и изотермического 2-0 (рисунок 9.1).

Рисунок 9.1 ‒ Обратимый переход системы в равновесие
с окружающей средой
Работа, которая может быть получена в открытой системе, равна располагаемой работе потока L0. В соответствии с первым законом термодинамики
 .
(9.1)
.
(9.1)
В рассматриваемом
случае
 .
Теплота отводится только в изотермическом
процессе, в котором
.
Теплота отводится только в изотермическом
процессе, в котором
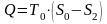 .
(9.2)
.
(9.2)
Учитывая, что в обратимом адиабатном процессе S=const и, следовательно, S1=S2, выражение для максимальной работы, т. е. для эксергии, может быть записано в виде
 .
(9.3)
.
(9.3)
Эксергия вещества в замкнутом объеме. Как и в случае открытой системы, единственным способом перехода закрытой системы в равновесие с окружающей средой является последовательность обратимых адиабатного и изотермического процессов (рисунок 9.1).
Максимальная полезная работа, которую можно получить от рассматриваемой закрытой системы, равна работе L изменения объема в указанных обратимых процессах за вычетом работы против сил давления окружающей среды
 .
(9.4)
.
(9.4)
Работа изменения объема в соответствии с первым законом термодинамики равна
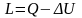 .
(9.5)
.
(9.5)
Как и в случае
открытой системы,
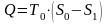 .
Тогда
.
Тогда
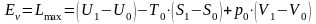 .
(9.6)
.
(9.6)
Эксергия потока теплоты. Эксергетическая температурная функция. Понятие эксергии потока теплоты основано на том, что за счет теплоты Q1, отбираемой от тела с температурой Т1, может быть получена работа в результате осуществления прямого цикла. Максимальная степень преобразования теплоты при заданной температуре окружающей среды Т0 может быть достигнута в обратимом цикле Карно, который осуществляется при температуре источника теплоты Т1 и температуре приемника Т0. Максимальная работа в этом цикле и, следовательно, эксергия потока теплоты равны
 .
(9.7)
.
(9.7)
В случае, когда температура источника теплоты переменна, эксергия потока теплоты может быть посчитана как
 ,
(9.8)
,
(9.8)
где dQ1 ‒ элементарное количество теплоты, отбираемое от источника при мгновенном значении его температуры Т1.
Величину
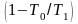 ,
представляющую собой КПД цикла Карно,
часто называют еще эксергетической
температурной функцией и обозначают
,
представляющую собой КПД цикла Карно,
часто называют еще эксергетической
температурной функцией и обозначают
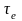 .
С учетом этого
.
С учетом этого
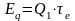 .
(9.9)
.
(9.9)
Для
тел, с температурой меньшей, чем Т0,
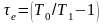 .
.
Зависимость эксергетической функции от температуры источника представлена на рисунке 9.2. Для оценки уровня отсчета эксергии используют температуру окружающей среды. При температуре источника, равной температуре приемника, функция равна нулю.

Рисунок 9.2 ‒ График зависимости эксергетической температурной
функции от температуры источника теплоты
Из графика видно,
что при
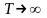 разница между
эксергией теплоты и работой становится
несущественной. При этом поток теплоты
может рассматриваться как поток
высококачественной энергии, равносильный
работе.
разница между
эксергией теплоты и работой становится
несущественной. При этом поток теплоты
может рассматриваться как поток
высококачественной энергии, равносильный
работе.
Большая зона
отрицательных значений функции
соответствует
относительно небольшому интервалу
температур от
 до Т0
К, что отражает более высокую эксергетическую
ценность потока теплоты почти во всей
зоне низких температур по сравнению с
таким же потоком при высоких температурах.
до Т0
К, что отражает более высокую эксергетическую
ценность потока теплоты почти во всей
зоне низких температур по сравнению с
таким же потоком при высоких температурах.
Изменение знака функции при переходе через Т0 приводит и к соответствующему изменению знака потока эксергии и потока теплоты. При температурах выше Т0 знаки одинаковы, т. е. направление потока эксергии совпадает с направлением потока теплоты. Если от системы отводится теплота, то отводится и эксергия. При температуре ниже Т0 знаки потоков эксергии и теплоты противоположны. Если от системы отводится теплота, то эксергия к ней будет подводиться.

Рисунок 9.3 ‒ Температурные зоны в области низких температур
Эксергетическая функция позволяет построить температурную шкалу, при использовании которой эксергия любого потока теплоты определяется эксергетической температурой (рисунок 9.3). Связь между температурами по эксергетической шкале и шкале Кельвина определяется уравнением (9.7).
Нулевая химическая эксергия. Нулевая химическая эксергия Е0 ‒ это максимальная работа, которая может быть получена в результате обратимой химической реакции при установлении термодинамического равновесия между продуктами реакции и теми же продуктами в окружающей среде при условии, что исходные и конечные продукты реакции имеют такие же значения температуры и давления, что и в окружающей среде.
В химических реакторах, в том числе в топочных устройствах, нулевая химическая эксергия является основной. Данные агрегаты рассматриваются как открытые термодинамические системы, для которых в случае обратимого течения процессов первый закон термодинамики можно записать в виде
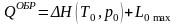 ,
(9.10)
,
(9.10)
где QОБР ‒ теплота, которая во время реакции обратимо, т. е. при Т0=const подводится к реакционной камере или отводится от нее; ΔН(Т0, р0) ‒ энтальпия реакции
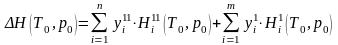 ,
(9.11)
,
(9.11)
где
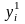 и
и
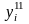 ‒ соответственно мольные (объемные)
доли исходных и конечных продуктов
реакции;
‒ соответственно мольные (объемные)
доли исходных и конечных продуктов
реакции;
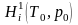 и
и
 ‒ энтальпии этих же продуктов при
температуре Т0
и давлении р0,
определяемые через энергию химических
связей.
‒ энтальпии этих же продуктов при
температуре Т0
и давлении р0,
определяемые через энергию химических
связей.
Энтальпия реакции равна теплоте реакции, взятой с обратным знаком. В случае топочного устройства ‒ это взятая с обратным знаком теплота сгорания топлива. Причем, если при Т0 и р0 вода в продуктах сгорания находится в газообразном состоянии, то речь идет о низшей теплоте сгорания QН, если в жидком ‒ о высшей QВ.
Окружающая среда с реакционной камерой образуют общую изолированную систему, для которой
 ,
(9.12)
,
(9.12)
где
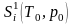 и
и
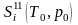 ‒ соответственно энтропии исходных и
конечных продуктов реакции;
‒ соответственно энтропии исходных и
конечных продуктов реакции;
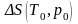 ‒ энтропия реакции.
‒ энтропия реакции.
Откуда
 .
(9.13)
.
(9.13)
Таким образом,
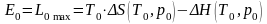 .
(9.14)
.
(9.14)
Поскольку
обычно
 ,
можно приближенно считать, что
,
можно приближенно считать, что
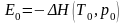 .
(9.15)
.
(9.15)
Эксергия излучения. Во многих реальных высокотемпературных системах значительную роль играет обмен энергией в форме излучения.
Эксергия собственного излучения идеально серой поверхности, приходящаяся на 1 м2 этой поверхности, равна
 ,
(9.17)
,
(9.17)
где С0=5,67∙10-8 Вт/(м2∙К4) ‒ постоянная Стефана-Больцмана; ε ‒ степень черноты излучающей поверхности.
При
 эксергия излучения пропорциональна
температуре и равна энергии излучения.
Если отношение
эксергия излучения пропорциональна
температуре и равна энергии излучения.
Если отношение
 ,
эксергия излучения меньше энергии
излучения, и наоборот. При малых значениях
Т0
значения эксергии и энергии излучения
сближаются.
,
эксергия излучения меньше энергии
излучения, и наоборот. При малых значениях
Т0
значения эксергии и энергии излучения
сближаются.
Эксергия собственного излучения не зависит от излучательной способности окружающей среды.
Параграф 10. Расчет эксергии и ее составляющих.
Изменение эксергии при физических и химических процессах. Расчет эксергии удобнее вести в удельных величинах. В общем случае эксергия является функцией параметров состояния (температуры, давления и состава среды)
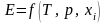 .
(10.1)
.
(10.1)
Приращение эксергии моля вещества при изменении температуры, давления и состава составляет
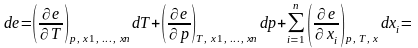
 ,
(10.2)
,
(10.2)
где еТ ‒ термическая эксергия; ер ‒ механическая эксергия давления; ехi ‒ химическая эксергия; сумма еТ+ер=еТМ ‒ термомеханическая или физическая эксергия.
При таком разделении эксергий можно при расчете термомеханической составляющей обойтись без знания значений эксергий чистых компонентов, но необходимо знать свойства смесей.
Дифференцируя уравнение
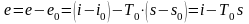 (10.3)
(10.3)
по температуре, давлению или по числу молей i-ого компонента, получим выражения для расчета соответствующих видов эксергии.
Термическая составляющая эксергии
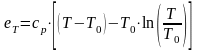 .
(10.4)
.
(10.4)
Если средняя удельная изобарная теплоемкость вещества сильно зависит от температуры, то она определяется как
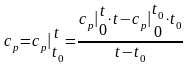 ,
(10.5)
,
(10.5)
где
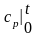 ,
,
 ‒ стандартные удельные изобарные
теплоемкости вещества при температурах
соответственно t
и t0.
‒ стандартные удельные изобарные
теплоемкости вещества при температурах
соответственно t
и t0.
При осуществлении процессов испарения или конденсации, а также плавления или кристаллизации из расплава, которые идут при постоянной температуре окружающей среды, термическая составляющая эксергии равна
 .
(10.6)
.
(10.6)
Механическая составляющая эксергии. Если рабочее тело ‒ идеальный газ, имеем
 ,
(10.7)
,
(10.7)
где
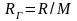 ‒ характеристическая газовая постоянная.
‒ характеристическая газовая постоянная.
Если же рабочее тело ‒ капельная жидкость, то
 ,
(10.8)
,
(10.8)
где β ‒ коэффициент объемного расширения жидкости; ρ ‒ плотность жидкости.
Химическая эксергии. В химических процессах изменение эксергии происходит за счет протекания химических превращений (тепловой эффект химических реакций), физических явлений (растворение, кристаллизация и др.) и за счет изменения состава смеси. Эксергия химических и физических явлений аналогична термической эксергии при фазовых превращениях. А эксергия, обусловленная изменением состава, аналогична эксергии давления, так как изменение состава проявляется в изменении парциального давления компонентов в газовой смеси и мольной доли в жидкой смеси.
С учетом этого химическая эксергия газовых смесей равна
 ,
(10.9)
,
(10.9)
pi и p0i ‒ парциальные давления i-ого компонента в рабочей и в окружающей среде соответственно
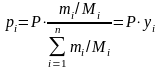 ,
(10.10)
,
(10.10)
где Р ‒ абсолютное давление газовой смеси; mi ‒ масса i-ого компонента; Мi ‒ молярная масса i-ого компонента; yi ‒ мольная доля i-ого компонента.
Химическая эксергия жидких смесей равна
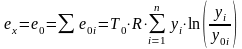 .
(10.11)
.
(10.11)
Существенный вклад в разработку методики точного расчета химической эксергии внес Я. Шаргут. В соответствии с ней сначала необходимо выбрать уровень отсчета. В качестве веществ отсчета Я. Шаргут для каждого химического элемента предложил принять наиболее распространенные в природе вещества, обладающие минимальной химической эксергией по отношению к другим веществам отсчета в окружающей среде, т. е. не вступающие с ними в реакцию окисления. Расчет проводят в следующем порядке.
Исходное вещество из состояния равновесия с окружающей средой переводят в нормальные условия и определяют его эксергию е1.
Определяют эксергию реакции девальвации е2, в процессе которой исходное вещество превращается в вещество отсчета, эксергия которого равна нулю.
Вычисляют эксергию е3, связанную с переводом веществ, участвующих в реакции девальвации, к расчетным условиям.
Суммарная эксергия ех=е1+е2+е3 и является химической эксергией вещества.
С точки зрения методики Я. Шаргута эксергию, рассчитанную по формулам (10.9) и (10.11) можно назвать остаточной химической эксергией, так как она содержит в своем составе только вещества отсчета. По своей сути она является термической эксергией веществ, участвующих в химическом процессе. Кроме того, расчету остаточной химической эксергии по этим формулам присущи неточности, возникающие, во-первых, из-за применения расчетных формул, справедливых для идеальных растворов, к реальным, а во-вторых, из-за неточности и неопределенности установления мольного содержания твердых веществ отсчета эксергии в окружающей среде.
Так как остаточная химическая эксергия, рассчитанная по формулам (10.9) и (10.11) состоит только из элементов, входящих в окружающую среду, в данном случае, она является нулевой химической эксергией. А поскольку эти формулы учитывают только изменение концентраций веществ, участвующих в химическом процессе, эту эксергию называют еще концентрационной составляющей химической эксергии. Знание этой составляющей позволяет оценить совершенство технологических процессов по получению соответствующих веществ из газовых смесей, жидких и твердых растворов. Ее численное значение характеризует минимально возможные энергозатраты на реализацию таких процессов.
Если же входные и выходные потоки эксергии анализируемой системы отличаются не только своими термодинамическими параметрами, но и составом, т. е. содержат разные вещества, полученные в результате химических взаимодействий, то в этом случае необходимо учитывать еще и реакционную составляющую химической эксергии. Эта составляющая является эксергией е2 согласно методике Я. Шаргута. Таким образом, химическая эксергия вещества в потоке в целом состоит из концентрационной и реакционной составляющих.
Рассмотрим основные соотношения для расчета эксергии потоков веществ, наиболее часто используемых в химической технологии в качестве энергоносителей.
Смесь идеальных газов. Физическую эксергию потока вещества, представляющего собой смесь идеальных газов, рассчитывают по формуле
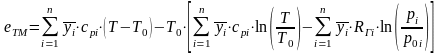 ,
(10.12)
,
(10.12)
где
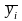 ‒ массовая доля i-ого
компонента; срi
‒ средняя удельная массовая изобарная
теплоемкость i-ого
компонента
‒ массовая доля i-ого
компонента; срi
‒ средняя удельная массовая изобарная
теплоемкость i-ого
компонента
 .
(10.13)
.
(10.13)
Если поток вещества является однокомпонентным идеальным газом, то формула (10.12) упрощается
 ,
(10.14)
,
(10.14)
где Р и Р0 ‒ абсолютные давления вещества в рабочей и в окружающей среде соответственно.
Вода и водяной пар. На практике используют воду и водяной пар, химический состав которых не отличается от состава этих веществ в окружающей среде. Поэтому расчет полной эксергии этих теплоносителей сводится к определению их термической и химической составляющих.
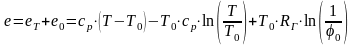 ,
(10.15)
,
(10.15)
где
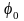 ‒ относительная влажность воздуха в
окружающей среды.
‒ относительная влажность воздуха в
окружающей среды.
Последнее слагаемое определяет термическую эксергию воды при давлении насыщения или насыщенного водяного пара при температуре окружающей среды, т. е. ее нулевую химическую эксергию.
Влажный воздух. Особенность расчета эксергии влажного воздуха состоит в том, что его состояние в окружающей среде не является постоянным. Атмосферный воздух всегда содержит водяные пары, количество которых меняется в зависимости от метеорологических условий. Для ряда технологических процессов наличие влаги в воздухе не имеет значения, и в этом случае атмосферный воздух можно рассматривать как абсолютно сухой. Однако при расчете сушильных установок, установок кондиционирования воздуха и т. п. необходимо учитывать наличие в воздухе водяных паров.
Влажный воздух можно рассматривать как смесь, состоящую из 1 кг абсолютно сухого воздуха и Х кг водяных паров. Соответственно эксергия такой смеси равна сумме эксергии воздуха еВ и водяных паров еП

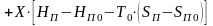 ,
(10.16)
,
(10.16)
где
индексы В
и П
относятся соответственно к воздуху и
водяному пару; Р
‒ полное давление;
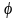 ‒ относительная влажность воздуха;
рS(t),
pS(t0)
‒ парциальные давления насыщенного
водяного пара соответственно при
температуре потока и в окружающей среде;
Х
‒ влагосодержание воздуха в потоке;
H
и S
‒ соответственно энтальпия и энтропия
пара.
‒ относительная влажность воздуха;
рS(t),
pS(t0)
‒ парциальные давления насыщенного
водяного пара соответственно при
температуре потока и в окружающей среде;
Х
‒ влагосодержание воздуха в потоке;
H
и S
‒ соответственно энтальпия и энтропия
пара.
При малых парциальных давлениях водяного пара его свойства близки к свойствам идеального газа. В этом случае влажный воздух можно рассматривать как смесь двух идеальных газов
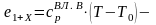
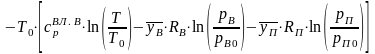 ,
(10.17)
,
(10.17)
где
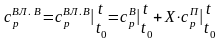 ;
(10.18)
;
(10.18)
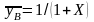 ,
,
 ;
(10.19)
;
(10.19)
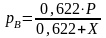 ,
,
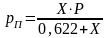 .
(10.20)
.
(10.20)
Топливо. Основную долю эксергии топлива составляет его химическая эксергия, так как на практике используют топливо с параметрами, равными параметрам окружающей среды. Для ряда газообразных и жидких органических веществ З. Рантом рассчитана их химическая эксергия:
для жидкого топлива, в молекуле которого содержится более одного атома углерода,
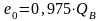 ;
(10.21)
;
(10.21)
для газообразного топлива, в молекуле которого содержится более одного атома углерода,
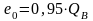 ;
(10.22)
;
(10.22)
для твердых топлив с учетом их влагосодержания W целесообразно их химическую эксергию принять равной их высшей теплотворной способности
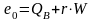 .
(10.23)
.
(10.23)
Теплотворная способность топлива может быть отнесена к рабочей массе топлива QР, т. е. к топливу в том виде, в каком оно поступает к потребителю; к сухой массе топлива QС; к горючей массе топлива QГ, т. е. к топливу, не содержащему влаги и золы. Связь между низшей и высшей теплотворными способностями выражается соотношением
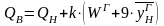 ,
(10.24)
,
(10.24)
где
k=25
кДж/кг; WГ
‒ влагосодержание топлива, отнесенное
к его горючей массе;
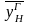 ‒ массовая доля водорода в горючей
массе топлива.
‒ массовая доля водорода в горючей
массе топлива.
Более точно эксергии топлив были рассчитаны Я. Шаргутом на основе разработанной им теории. При этом для основных элементов, входящих в состав всех топлив (С, Н, N, О), в качестве веществ отсчета были взяты газы, входящие в состав атмосферного воздуха, что упростило расчет. Для углеводородных соединений различных групп существуют корреляционные формулы, представляющие собой отношение химической эксергии к высшей теплотворной способности.
Для твердых технических топлив это отношение рассчитывают по формуле
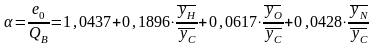 .
(10.25)
.
(10.25)
Для топлив, содержащих серу, необходимо ввести поправку. Для серы в качестве вещества отсчета выбран гипс CaSO4∙2H2O. Химическая эксергия серы значительно выше ее теплотворной способности. Разность этих величин, отнесенная к 1 кг серы, составляет
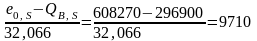 кДж/кг.
кДж/кг.
Полная формула для расчета химической эксергии твердого топлива имеет вид
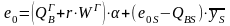 ,
(10.26)
,
(10.26)
где r ‒ удельная теплота парообразования воды.
Для жидких технических топлив
 ,
(10.27)
,
(10.27)
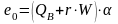 .
(10.28)
.
(10.28)
Для газообразных топлив расчетные формулы Я. Шаргута имеют вид:
для коксового газа
 ;
(10.29)
;
(10.29)
для колосникового газа
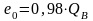 ;
(10.30)
;
(10.30)
для генераторного газа
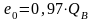 ;
(10.31)
;
(10.31)
для природного газа
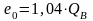 .
(10.32)
.
(10.32)
Также для расчета химической эксергии углей различных марок и жидких топлив соответственно предложены эмпирические формулы
 ,
(10.33)
,
(10.33)
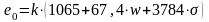 ,
(10.34)
,
(10.34)
где
k=7,817
кДж/кг;
 ;
;
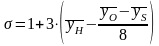 .
.
В большинстве случаев на практике температура топлива близка к температуре окружающей среды, и нет необходимости учитывать термическую составляющую эксергии. Исключение составляет тяжелое жидкое топливо (мазут), которое для снижения его вязкости подогревают до 70÷100 °С. В этом случае термическую эксергию топлива определяют с использованием усредненных значений характеристик его компонентов.
Дымовые газы. В состав дымовых газов входят СО2, СО, SO2, SO, H2S, Н2О, N2O2. При большом избытке воздуха, обычном для промышленных топок и печей, не должно быть продуктов неполного сгорания топлив (СО, SO). В большинстве случаев содержание серы в дымовых газах незначительно, а при сжигании природных газов равно нулю, поэтому им можно пренебречь. Таким образом, в дымовых газах остаются СО2, N2, O2, Н2О. Все эти вещества содержатся в воздухе, но в других количествах. Поэтому химическая эксергия дымовых газов рассчитывается по формулам (10.9), (10.11).
Для многих теплоиспользующих установок дымовые газы следует рассматривать не самостоятельно, а совместно с топливом и продуктами сгорания, которыми они и являются. Состав таких дымовых газов и их термодинамические параметры зависят от течения процесса горения исходного топлива. В этом случае мольную химическую эксергию дымовых газов, приходящуюся на 1 кмоль сухих продуктов сгорания топлива, определяют по формуле
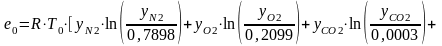
 ,
(10.35)
,
(10.35)
где ХZ ‒ мольное влагосодержание продуктов сгорания; X0 ‒ мольное влагосодержание воздуха в окружающей среде.
Если химическую эксергию отнести к 1 кмоль влажных продуктов сгорания, то расчетная формула примет вид
 .
(10.36)
.
(10.36)
Термомеханическую составляющую эксергии дымовых газов можно определить по формуле (10.12) для расчета физической эксергии вещества в потоке, представляющего собой смесь идеальных газов. При этом используют среднюю теплоемкость компонентов в интервале температур от температуры окружающей среды до теоретической температуры горения
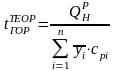 ,
(10.37)
,
(10.37)
где
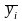 ‒ массовая доля i-ого
продукта сгорания; сpi
‒ средняя удельная массовая изобарная
теплоемкость i-ого
продукта сгорания.
‒ массовая доля i-ого
продукта сгорания; сpi
‒ средняя удельная массовая изобарная
теплоемкость i-ого
продукта сгорания.
Для большинства промышленных топок давление дымовых газов равно атмосферному. В этом случае механическая составляющая физической эксергии будет равна нулю.
Параграф 11. Закон Гюи-Стодолы.
Эксергия есть
максимальная работа, которая совершается
при обратимом переходе системы в
равновесие с окружающей средой. Наличие
необратимости приводит к уменьшению
работы, т. е. потере части эксергии.
Рассмотрим теплосиловую установку,
которая представляет собой открытую
систему (рисунок 11.1). В установку вводится
рабочее тело с параметрами H1,
S1
и теплота Q1
от источника теплоты с температурой Т.
Из установки рабочее тело выходит с
параметрами Н2
и S2.
Теплота
 от установки отводится в окружающую
среду с температурой Т0.
Полезная работа для этой термодинамической
системы будет определяться как
от установки отводится в окружающую
среду с температурой Т0.
Полезная работа для этой термодинамической
системы будет определяться как
 .
(11.1)
.
(11.1)
Для сравнению возьмем установку, в которой при тех же параметрах рабочего тела на входе и выходе все процессы протекают обратимо. Вследствие обратимости совершаемая работа станет максимально возможной
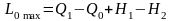 ,
(11.2)
,
(11.2)
где Q0 ‒ теплота, отводимая в окружающую среду при обратимом течении процессов в установке.

Рисунок 11.1 ‒ Схема потоков вещества и энергии в
теплосиловой установке
Тогда потери работоспособности, вызванные необратимостью, составят
 .
(11.3)
.
(11.3)
При
этом следует учитывать, что при отводе
теплоты
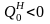 и
и
 .
.
Суммарные приращения энтропии рабочего тела и окружающей среды при необратимом и обратимом протекании процессов в установке будут соответственно равны
 ,
(11.4)
,
(11.4)
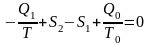 .
(11.5)
.
(11.5)
Вычитая (11.5) из (11.4), получим выражение для потерь работоспособности вследствие необратимости
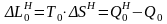 .
(11.6)
.
(11.6)
Покажем, что формула (11.6) является универсальной и выражает потери работоспособности или эксергии вследствие любого вида необратимости. Рассмотрим работу ХТС в стационарном, установившемся режиме. Давление в системе не меняется, т. е. работа не совершается (рисунок 11.2). На вход системы подаются потоки эксергии, из системы с уходящими потоками эксергия уходит из ХТС.

Рисунок 11.2 ‒ К выводу закона Гюи-Стодолы
В соответствии с
первым законом термодинамики в любом
процессе
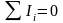 .
В обратимом процессе
.
В обратимом процессе
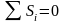 .
Следовательно, в этом случае эксергия
не теряется, т. е.
.
Следовательно, в этом случае эксергия
не теряется, т. е.
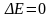 .
В реальной процессе
.
В реальной процессе
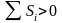 .
.
Исходя из современных представлений физического смысла понятия эксергии, суммарная эксергия потоков на входе в ХТС
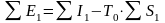 ,
(11.7)
,
(11.7)
на выходе из ХТС
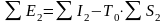 ,
(11.8)
,
(11.8)
а изменение эксергии в ходе протекающих в ХТС процессов равно
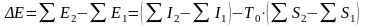 .
(11.9)
.
(11.9)
Поскольку
всегда
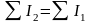 ,
то
,
то
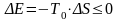 .
(11.10)
.
(11.10)
Это уравнение, показывающее, что эксергия убывает пропорционально энтропии, называется законом Гюи-Стодолы. Оно показывает, какое количество работы безвозвратно теряется вследствие нерационального аппаратурно-технологического оформления процесса или из-за принципиальных его особенностей, приводящих к термодинамической необратимости.
Закон Гюи-Стодолы позволяет вычислить потери эксергии как в любых ХТС в целом, так и в отдельных ее элементах. В последнем случае общие потери получаются путем суммированием потерь в элементах.
Параграф 12. Баланс эксергии. Диаграмма Грассмана-Шаргута.
Эксергия не подчиняется закону сохранения. В ходе любого необратимого процесса часть ее безвозвратно теряется, переходя в анергию. Поэтому, строго говоря, не существует баланса между, с одной стороны, эксергией, подводимой к системе, и, с другой стороны, суммой отводимой эксергии и изменения эксергии тел, образующих систему. Однако такой баланс можно свести искусственно, если учитывать потери эксергии. Для установок непрерывного действия при установившемся режиме их работы составленный таким образом баланс в общем виде имеет вид
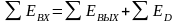 ,
(12.1)
,
(12.1)
где
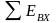 ,
,
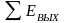 ‒ суммы
потоков эксергии, поступающих в систему
и уходящих из нее;
‒ суммы
потоков эксергии, поступающих в систему
и уходящих из нее;
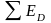 ‒ сумма потерь эксергии в системе.
‒ сумма потерь эксергии в системе.
Если использовать введенное профессором Г.Н. Костенко понятие транзитной эксергии ЕТР, т. е. эксергии, которая проходит от входа в установку до выхода из нее, не участвуя в процессах преобразования энергии, то эксергетический баланс можно записать иначе
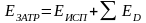 ,
(12.2)
,
(12.2)
где ЕЗАТР и ЕИСП ‒ соответственно затраченная и использованная эксергии
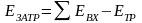 ,
(12.3)
,
(12.3)
 .
(12.4)
.
(12.4)
Обычно транзитом
эксергии сопровождаются процессы
преобразования энергии с участием
потоков рабочих тел. Например, процессы
в теплообменных аппаратах, компрессорных
машинах, смесительных и разделительных
устройствах, трубопроводах. При отсутствии
в установке транзита эксергии выражения
(12.1) и (12.2) становятся тождественными,
т. е.
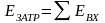 и
и
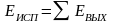 .
.
Рассмотрим баланс эксергии для котлоагрегата, технологическая схема которого представлена на рисунке 12.1.

Т ‒ топка; К ‒ котлоагрегат; П ‒ воздухоподогреватель; Э ‒ экономайзер
Рисунок 12.1 ‒ Технологическая схема котлоагрегата
Наглядно эксергетический баланс может быть представлен в виде диаграммы Грассмана-Шаргута (рисунок 12.2). На диаграмме ширина полос в условном масштабе соответствует потокам эксергии. Полосы, соответствующие потерям эксергии вследствие необратимости какого-либо процесса, заштрихованы.

ЕТ
‒ эксергия топлива; ЕВ
‒ эксергия воздуха;
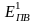 ,
,
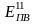 ‒ эксергия
питательной воды на входе и соответственно
на выходе из экономайзера;
‒ эксергия
питательной воды на входе и соответственно
на выходе из экономайзера;
ЕГП ‒ эксергия продуктов сгорания после воздухоподогревателя;
ЕГЭ ‒ эксергия продуктов сгорания после экономайзера; ЕУХ ‒ уходящая
из
системы эксергия; ЕП
‒ эксергия полученного пара;
 ,
,
 ‒ суммарная
‒ суммарная
эксергия на входе и соответственно на выходе из воздухоподогревателя;
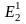 ,
,
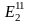 ‒ суммарная эксергия на входе и
соответственно на выходе из
‒ суммарная эксергия на входе и
соответственно на выходе из
топки;
 ,
,
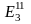 ‒ суммарная
эксергия на входе и соответственно на
выходе
‒ суммарная
эксергия на входе и соответственно на
выходе
из котлоагрегата; ЕD1, ЕD2, ЕD3, ЕD4 ‒ потери эксергии соответственно в
воздухоподогревателе, в топке, в котлоагрегате и в экономайзере;
ЕD5 ‒ потери эксергии с уходящими газами
Рисунок 12.2 ‒ Диаграмма Грассмана-Шаргута для котлоагрегата
Эксергия на входе в котлоагрегат складывается из эксергии топлива ЕТ, воздуха ЕВ и питательной воды . Обычно воздух перед подачей в топку (Т) подогревают теплотой уходящих газов в воздухоподогревателе (П). Процесс теплообмена в воздухоподогревателе сопровождается потерями эксергии ЕD1. Суммарная эксергия на входе в топку равна
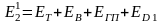 .
(12.5)
.
(12.5)
Процесс преобразования эксергии в топке сопровождается потерями эксергии ЕD2, и поток продуктов сгорания на выходе из топке обладает эксергией . Продукты сгорания передают теплоты воде и пару в газоходах котлоагрегата (К). Вследствие конечной разности температур между продуктами сгорания, с одной стороны, и паром, с другой, передача теплоты сопровождается потерями эксергии ЕD3.
Питательная вода, поступающая в котлоагрегат, обладает эксергией . Как правило, на входе в котлоагрегат она подогревается в экономайзере (Э) теплотой уходящих газов. В процессе теплообмена в экономайзере теряется эксергия ЕD4. В итоге после основных поверхностей теплообмена котельного агрегата суммарный поток эксергии равен
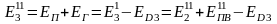 ,
(12.6)
,
(12.6)
где
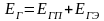 .
.
Часть эксергии ЕГ возвращается в котлоагрегат через воздухоподогреватель и экономайзер, а оставшаяся часть ЕУХ = ЕD5 теряется вместе с продуктами сгорания, выбрасываемыми в атмосферу.
Эксергия пара ЕП представляет собой полезную эксергию, получаемую в котлоагрегате.
Параграф 13. Энергетический метод термодинамического анализа ХТС.
Энергетический метод анализа основывается на первом законе термодинамики, в соответствии с которым подведенные к установке теплота и работа и отведенные теплота и работа должны равняться друг другу
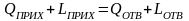 .
(13.1)
.
(13.1)
Рассмотрим в качестве примера тепловой баланс печей химической промышленности, приходную часть которого можно выразить как
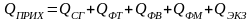 ,
(13.2)
,
(13.2)
где QСГ ‒ теплота, выделившаяся при сгорании топлива и равная произведению израсходованной массы топлива и его низшей теплоты сгорания; QФТ ‒ физическая теплота (энтальпия) топлива; QФВ ‒ физическая теплота (энтальпия) воздуха, подаваемого в печь; QФМ ‒ физическая теплота (энтальпия) технологического материала, загружаемого в печь; QЭКЗ ‒ теплота, выделяющаяся в результате экзотермических реакций, протекающих в технологическом материале.
Расходная часть теплового баланса
 ,
(13.3)
,
(13.3)
где
QПР
‒ теплота, равная энтальпии продуктов
переработки технологического материала;
QЭНД
‒ теплота, затраченная на эндотермические
реакции переработки технологического
материала; QУХ
‒ потеря теплоты с уходящими газами;
QХН
‒ потеря теплоты от химической неполноты
сгорания топлива; QМН
‒ потеря теплоты от механической
неполноты сгорания топлива; QОХ
‒ потеря теплоты в окружающую среду
через стенки печи;
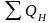 ‒
сумма прочих тепловых потерь.
‒
сумма прочих тепловых потерь.
Здесь термин «потери энергии» носит условный характер, так как в соответствии с законом сохранения энергия не может исчезать и возникать.
Первые два слагаемых расходной части можно назвать полезно использованной теплотой, так как ради них и работает технологическая печь, выдающая внешнему потребителю продукт переработки исходного технологического материала
 .
(13.4)
.
(13.4)
Остальные слагаемые рассматриваются как потери теплоты
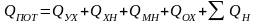 .
(13.5)
.
(13.5)
В идеальном случае, когда потери отсутствуют
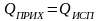 .
(13.6)
.
(13.6)
В реальных условиях полезная теплота составляет лишь некоторую долю приходной части теплового баланса, остальная энергия расходуется на покрытие потерь теплоты
 .
(13.7)
.
(13.7)
Долю приходной части теплового баланса, используемую непосредственно в качестве полезной теплоты, называют эффективным КПД, который представляет собой отношение количества энергии (в форме теплоты или работы), полученной внешним потребителем, к количеству энергии (в форме теплоты или работы), подведенной к установке
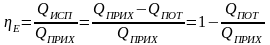 .
(13.8)
.
(13.8)
Все описанное выше можно представить графически в виде диаграммы потоков энергии (рисунок 13.1). Такие диаграммы называются диаграммами Сенкея.

Рисунок 13.1 ‒ Диаграмма Сенкея для технологической печи
В общем случае эффективный КПД учитывает и внутреннюю и внешнюю необратимости. Потери энергии, обусловленные как той, так и другой необратимостью, могут быть охарактеризованы своими КПД. Рассмотрим это на примере паросиловой установки (ПСУ), обеспечивающей в ХТС привод компрессорной машины.
Анализ начинается с определения энергетической эффективности, которая имела бы место при обратимом протекании всех процессов в цикле ПСУ. Эта эффективность характеризуется термическим КПД
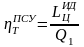 ,
(13.9)
,
(13.9)
где
 ‒ работа,
которая была бы получена в идеальном
цикле; Q1
‒ подведенная за цикл теплота.
‒ работа,
которая была бы получена в идеальном
цикле; Q1
‒ подведенная за цикл теплота.
Из-за потерь, обусловленных внутренней необратимостью, работа, производимая паром за цикл в ПСУ и называемая внутренней работой Li, оказывается меньше . Отношение внутренней работы к подведенной за цикл теплоте называется внутренним КПД
 ,
(13.10)
,
(13.10)
а отношение
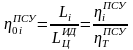 (13.11)
(13.11)
‒ относительным внутренним КПД, характеризующим потери работы, вызванные внутренней необратимостью.
Потребитель, в данном примере это компрессор, получает за цикл эффективную работу LE, меньшую, чем Li. Это обусловлено внешней необратимостью: трением в подшипниках валов, затратами энергии на привод вспомогательных устройств и т. д. Потери работы вследствие внешней необратимости оцениваются механическим КПД
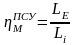 .
(13.12)
.
(13.12)
Эффективным КПД ПСУ называется отношение
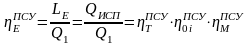 .
(13.13)
.
(13.13)
Если требуется
оценить эффективный КПД всего
энергетического блока ХТС (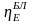 ),
включающего ПСУ и компрессоры, то
необходимо дополнительно учесть
эффективный КПД компрессора (
),
включающего ПСУ и компрессоры, то
необходимо дополнительно учесть
эффективный КПД компрессора (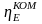 )
)
 .
(13.14)
.
(13.14)
В общем случае при наличии n элементов в энергетическом блоке его эффективный КПД определяется как
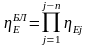 .
(13.15)
.
(13.15)
Рассмотрение энергетического метода позволяет прийти к следующим важным выводам.
При определении суммарных количеств подведенной и отведенной энергии необходимо контролировать их равенство.
Метод позволяет оценить потери энергии в ХТС, определить потери энергии по всей ХТС и отдельным ее элементам, выявить те элементы, где теряется наибольшее количество энергии.
Это единственный метод термодинамического анализа, позволяющий определить потери тепловой энергии через внешнюю поверхность установки в окружающую среду.
Недостатком метода является то, что в нем не учитывается качество энергии т. е. ее превратимость в работу, так как из второго закона термодинамики следует, что одно и то же количество энергии может обладать разной работоспособностью (эксергией).
Параграф 14. Эксергетические показатели эффективности тепловых процессов.
В отличии от энергетического энтропийный и эксергетический методы анализа базируются на обоих законах термодинамики. Они учитывают как сохранение количества энергии, так и изменение ее качества, т. е. соотношение между эксергией и анергией. Эксергетические представления обеспечивают полноту и объективность термодинамического совершенства ХТС и ее отдельных процессов. Для оценки эффективности работы теплоиспользующего оборудования предложен ряд показателей, учитывающих особенности протекающих в нем процессов при наличии транзита эксергии.
Степень использования эксергии, т. е. эксергетический КПД можно получить из уравнения баланса эксергии
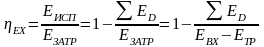 .
(14.1)
.
(14.1)
Степень термодинамического совершенства показывает, насколько реальный процесс близок к идеальному, т. е. обратимому
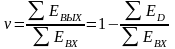 .
(14.2)
.
(14.2)
Кроме того, существуют еще два критерия оценки совершенства тепловых процессов:
степень технологического совершенства
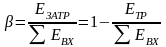 ;
(14.3)
;
(14.3)
степень полного совершенства
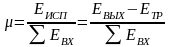 .
(14.4)
.
(14.4)
Выбор определяющего
показателя эффективности во многом
зависит от характера рассматриваемой
задачи. Чаще всего наибольший интерес
представляют величины
 или
,
так как они учитывают и потери, и
транзитную эксергию.
или
,
так как они учитывают и потери, и
транзитную эксергию.
Все указанные показатели связаны следующими соотношениями
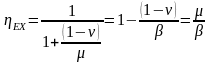 ,
(14.5)
,
(14.5)
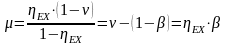 .
(14.6)
.
(14.6)
Для процессов, в
которых есть транзит эксергии
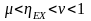 .
Для бестранзитных процессов, например
механических,
.
Для бестранзитных процессов, например
механических,
 .
.
Для термодинамических
идеальных обратимых процессов всегда
 ,
но при ЕТР>0
оказывается
,
но при ЕТР>0
оказывается
 .
.
Параграф 15. Энтропийный метод термодинамического анализа ХТС.
Энтропийный метод представляет собой развитие «метода вычитания» эксергетических потерь из эксергии теплоты, подведенной к ХТС. Данный метод вычисляет эксергию теплоты только на входе в рассматриваемый узел установке или установку в целом. Однако, если установка должна отдавать часть теплоты для полезного использования на технологические нужды, отопление и т. д., то целесообразно вычислить эксергию и этой теплоты.
Энтропийный метод применим к тем ХТС (утилизационным тепловым установкам, абсорбционным холодильным машинам и т. д.), в которых энергия к ним подводится в форме теплоты (утилизируемая теплота продуктов технологического процесса, отработавшего пара или горячей воды). В реальных условиях в установку часто вводится «организованная энергия»: механическая работа, химическая энергия топлива, электрическая, ядерная энергия. Энтропийный метод применим и в этом случае.
Зная потери эксергии в каждом элементе ХТС, можно составить для нее эксергетический баланс, диаграмма которого изображена на рисунке 15.1.
Для энергетических силовых установок, технологических печей и т. п. входящая эксергия ЕВХ представляет собой «организованную энергию», введенную в установку: химическую энергию топлива, энергию исходных продуктов экзотермических реакций, ядерную энергию, электроэнергию и т. д.
Для компрессорных холодильных установок ЕВХ ‒ это электрическая или механическая энергия, подведенная к компрессорам.
Для холодильных абсорбционных установок ЕВХ ‒ эксергия теплоты, подведенной к парогенератору.
Для теплонаносных установок ЕВХ включает в себя сумму электрической энергии, которая целиком состоит из эксергии, и эксергии утилизируемой теплоты.
Для теплообменных аппаратов ЕВХ ‒ эксергия подведенной к аппарату теплоты.

n ‒ элементы ХТС; EDi ‒ потери эксергии в соответствующем элементе ХТС
Рисунок 15.1 ‒ Схема эксергетического баланса по энтропийному методу
Потери эксергии в каждом элементе ХТС при энтропийном методе подсчитываются по формуле Гюи-Стодолы
 ,
(15.1)
,
(15.1)
где Т0 ‒ температура окружающей среды; ΔSi ‒ увеличение энтропии в элементе ХТС, включая изменение энтропии при переходе «организованной энергии» в теплоту.
Если система вследствие теплообмена с окружающей средой передает ей теплоту Q0, то это вызывает изменение энтропии окружающей среды
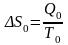 .
(15.2)
.
(15.2)
Рассматривая систему и окружающую среду как единую изолированную систему, к суммарному изменению энтропии в системе необходимо добавить изменение энтропии окружающей среды. Тогда общие потери эксергии составят
 .
(15.3)
.
(15.3)
Следует отметить, что механические потери, т. е. потери, связанные с трением в элементах системы, и электрические потери непосредственно передаются окружающей среде в виде теплоты Q0.
Основой энтропийного метода является вычисление абсолютных коэффициентов эксергетических потерь в каждом из элементов установки
 .
(15.4)
.
(15.4)
Эти коэффициенты называются абсолютными потому, что при их вычислении потери эксергии в элементе относят к эксергии, затраченной в установке в целом.
Абсолютный коэффициент эксергетических потерь всей установки равен сумме абсолютных коэффициентов эксергетических потерь во всех ее элементах
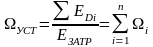 ,
(15.5)
,
(15.5)
что дает возможность оценить влияние необратимостей в установке на эффективность использования затраченной эксергии, ее перерасход.
Отсюда эксергетический КПД ХТС или ее отдельного элемента равен
 .
(15.6)
.
(15.6)
Данная формула лежит в основе энтропийного метода термодинамического анализа.
Для энергетической установки, предназначенной только для получения работы, электроэнергии или потенциальной энергии сжатых газов, т. е. не имеющей функции теплоснабжения, эксергетический КПД совпадает с эффективным КПД.
Пусть, например, в установке затрачивается химическая эксергия топлива
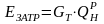 ,
(15.7)
,
(15.7)
где
GТ
‒
расход топлива в единицу времени;
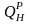 ‒
низшая теплота сгорания топлива.
‒
низшая теплота сгорания топлива.
Тогда эксергетический КПД этой установки будет равен
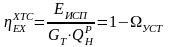 ,
(15.8)
,
(15.8)
а расход топлива определится как
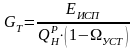 .
(15.9)
.
(15.9)
В идеальной установке, т. е. в установке, где все процессы обратимы, абсолютный коэффициент потери эксергии равен нулю. В этом случае расход топлива составит
 .
(15.10)
.
(15.10)
Разность
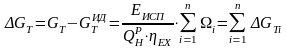 (15.11)
(15.11)
дает значение перерасхода ΔGТ топлива по сравнению с идеальной установкой, обусловленного необратимым течением процессов, т. е. перерасход топлива тем больше, чем меньше эксергетический КПД установки и выше коэффициент эксергетических потерь. Данная формула позволяет оценивать величины перерасхода, обусловленные необратимостью процессов в каждом отдельном элементе или узле ХТС.
Рассмотрение энтальпийного метода позволяет перийти к следующим важным выводам.
Система коэффициентов эксергетических потерь универсальна для любой энергетической, холодильной или теплонаносной установки.
Основные показатели метода характеризуют термодинамическое совершенство установки (эксергетический КПД), а также суммарную потерю производимой и затрачиваемой в установке работы вследствие необратимости процессов (сумма абсолютных коэффициентов эксергетических потерь).
Недостатком метода является учет только относительных потерь эксергии отдельных элементов ХТС, которые не дают представления о термодинамической эффективности конкретного элемента как самостоятельного объекта.
Параграф 16. Эксергетический метод термодинамического анализа ХТС.
Эксергетический метод термодинамического анализа ХТС, как и энтропийный, опирается на оба закона термодинамики и позволяет оценить не только количество, но и изменение качества энергии ‒ ее превратимость (эксергию).
Универсальность этого метода заключается в том, что характер процессов анализируемой системы не имеет принципиального значения, так как подход к решению задачи и метод ее решения не изменяется. Каждый элемент ХТС рассматривается как самостоятельная термодинамическая система. Эффективность работы каждого элемента оценивается путем сравнения эксергии на входе в этот элемент с потерей работоспособности в нем, т. е. с потерей эксергии в результате осуществления необратимых процессов в этом элементе. При определении потерь эксергии в каждом элементе исследуемой ХТС выявляются и количественно оцениваются причины несовершенства протекающих в них процессов, что дает информацию о возможности повышения совершенства во всех элементах и позволяет создать наиболее совершенную ХТС. Это является основной целью эксергетического метода анализа ХТС.
Эксергетический анализ применяется для рассмотрения открытых систем, а именно таких, которые обмениваются с другими системами, в том числе и с окружающей средой, не только энергией, но и веществом. Классическая термодинамика рассматривает обычно только закрытые системы. В этом случае закрытую систему рассматривают как совокупность открытых систем, в отдельных частях которой состав может изменяться, однако в целом в системе материальный баланс по каждому компоненту сохраняется.
В эксергетическом анализе применяется аналогичный прием. Технический объект рассматривается как первая подсистема, а окружающая среда есть вторая подсистема закрытой в целом системы. Две подсистемы обмениваются между собой энергией и веществом при сохранении материального баланса в целом по системе.
Многообразие вариантов расчета эксергии объясняется не только сложностью задачи, но и нередко ошибками принципиального характера. Уточним некоторые основные понятия, от которых зависит корректность подхода к решению задач.
Окружающая среда. Для анализа каждого процесса выбирается конкретная окружающая среда (т. е. конкретные уровни отсчета эксергии). Состав ее может и не соответствовать составу какой-либо природной среды (хотя это и желательно). В эксергетическом методе анализа к окружающей среде предъявляется ряд требований.
Независимость ее основных параметров (температура, давление, состав) от рассматриваемой технической системы. Следовательно, окружающая среда является бесконечно большим резервуаром веществ по сравнению с технической системой. При этом эксергия окружающей среды не изменяется при добавлении к ней (или изъятии из ее запаса) веществ отсчета. Таким образом, параметры окружающей среды не зависят от ее взаимодействия с системой.
Максимальная близость значений основных параметров окружающей среды к значениям параметров окружающей природы. Так температуру окружающей среды обычно принимают равной Т0=293 К, а давление р0=0,1 МПа. В тех случаях, когда это возможно, состав окружающей среды принимают таким же, каков состав соответствующей природной среды, например атмосферы.
Изобарно-изотермический потенциал веществ отсчета (продуктов химических реакций) должен быть минимален или равен нулю. Окружающая среда обладает минимальной свободной энергией, являясь приемником продуктов процесса (вещества и энергии) и источником сырья. Сама по себе окружающая среда не может быть источником работы. Таким образом, необходимо рассматривать такую окружающую среду, для создания которой не требуется затрачивать работу.
Компоненты среды должны находиться между собой в термодинамическом равновесии. Поскольку в окружающей природной среде не существует абсолютного равновесия, то всегда в явном или скрытом виде некоторые процессы заторможены, т. е. их скоростью можно пренебречь по сравнению со скоростью реальных, незаторможенных процессов. Условия заторможенности должны быть оговорены. Аналогично должен быть оговорен ограниченный круг процессов и реакций, которые протекают (или могут протекать) в анализируемой системе.
Уровни отсчета эксергии. С целью облегчения выбора уровней отсчета эксергии многообразные технические процессы можно разделить на четыре группы.
1. Физические процессы, при которых не изменяется состав рабочих тел. Например процессы сжатия, нагревания веществ, сжижения газов и т. д., протекающие в закрытых системах.
2. Процессы, при которых происходит изменение концентрации компонентов, но не протекают химические превращения (т. е. не появляются новые вещества). Например, многие процессы разделения смесей.
3. Химические процессы, т. е. процессы, в которых образуются новые молекулы.
4. Ядерные реакции, т. е. процессы, в которых появляются новые атомы.
Для анализа процессов первой группы задача выбора уровня отсчета эксергии (или, что то же самое, окружающей среды) значительно упрощается. В этом случае достаточно знать параметры окружающей природной среды T0 и р0.
Для процессов второй группы веществами отсчета эксергии могут быть сами компоненты системы. Эти процессы можно подразделить на две подгруппы.
Первая подгруппа включает все процессы, используемые для подготовки сырья к химическому превращению, и поэтому в составе не могут присутствовать вещества, которых нет в сырье. Расчет эксергии для этих процессов ведут так же, как и для процессов первой группы.
Вторая подгруппа
включает процессы выделения из продуктов
химического превращения целевых веществ.
В их составе присутствуют вещества,
которых нет в сырье. Расчет эксергии
для этих процессов ведут с использованием
допущения о «заторможенности» процессов
получения полезной работы при смешении
веществ в отсутствии теплового эффекта.
Тогда точкой отсчета при расчете эксергии
смеси будет
 МПа. Здесь необходимо рассчитывать
эксергию не компонента, а смеси в целом
через ее приращение в результате
изменения температуры и давления.
МПа. Здесь необходимо рассчитывать
эксергию не компонента, а смеси в целом
через ее приращение в результате
изменения температуры и давления.
Для процессов третьей группы расчет эксергии ведут с учетом химической составляющей. При этом необходимо учитывать только те реакции, которые протекают (или могут протекать) в данной системе. Такой подход оправдан, но связан с определенными трудностями, так как ХТС состоит из нескольких последовательных технологических процессов, относящихся к разным группам. При постадийном эксергетическом анализе с использованием различных уровней отсчета значения эксергии одного и того же потока вещества будут различны для различных стадий. Эта проблема снимается при расчете разностей эксергии, значения которых не зависят от уровня отсчета, т. е. при оценке эффективности процесса по «разностным» или «целевым» эксергетическим КПД.
Таким образом, основным показателем, которым оперирует эксергетический анализ, является эксергетический КПД. В отличии от энтропийного анализа здесь полезный эксергетический эффект и затраты эксергии определяются непосредственно (например, как эксергия потока вещества или эксергия потока теплоты), а потери эксергии находятся как разность
 .
(16.1)
.
(16.1)
Объективность эксергетического анализа зависит от правильности определения потоков эксергии: затраченной и использованной.
Обобщенной характеристикой, позволяющей оценить степень работоспособности потоков всех видов энергии любой ХТС является эксергетическая производительность (мощность)
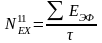 ,
(16.2)
,
(16.2)
где
 ‒ сумма
эффективных потоков эксергии, определяющая
полученный эффект, даваемый системой
(сумма эксергий только тех продуктов,
которые будут использоваться в дальнейшем
технологическом процессе, т. е. всех,
кроме побочных, эксергия которых является
бросовой);
‒ сумма
эффективных потоков эксергии, определяющая
полученный эффект, даваемый системой
(сумма эксергий только тех продуктов,
которые будут использоваться в дальнейшем
технологическом процессе, т. е. всех,
кроме побочных, эксергия которых является
бросовой);
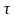 ‒ время (в
секундах, минутах или часах).
‒ время (в
секундах, минутах или часах).
Точно также как и мощность, можно определить потребление системы, т. е. суммарное количество эксергии, которую она потребляет в единицу времени
 .
(16.3)
.
(16.3)
При этом эксергетический КПД можно рассчитать по уравнению
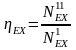 .
(16.4)
.
(16.4)
Проиллюстрируем подходы эксергетического метода анализа на примере охлаждаемого компрессора с использованием понятия транзита эксергии.
Баланс эксергии имеет вид
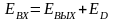 ,
(16.5)
,
(16.5)
а именно
 ,
(16.6)
,
(16.6)
где Е1 и Е2 ‒ соответственно эксергии потока рабочего тела на входе и на выходе из компрессора; L ‒ действительная работа, затраченная на привод компрессора; Еq ‒ эксергия потока теплоты, выделяемая при сжатии рабочего тела; ЕD ‒ потери эксергии;
Если в компрессоре эксергия Eq используется полезно, то баланс эксергии примет вид
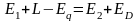 .
(16.7)
.
(16.7)
В компрессоре имеет место транзит эксергии
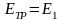 .
(16.8)
.
(16.8)
В связи с этим,
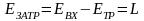 ,
(16.9)
,
(16.9)
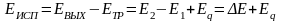 .
(16.10)
.
(16.10)
В случае, когда теплота сжатия используется полезно
 ,
(16.11)
,
(16.11)
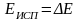 .
(16.12)
.
(16.12)
Эксергетический КПД охлаждаемого компрессора равен
 .
(16.13)
.
(16.13)
Эксергетическая производительность (мощность) охлаждаемого компрессора равна
 ,
(16.14)
,
(16.14)
где G ‒ расход рабочего тела; Δе ‒ возрастание эксергии рабочего тела в процессе сжатия.
Если теплота сжатия используется полезно, то ее эксергию также необходимо учесть
 ,
(16.15)
,
(16.15)
где GВ ‒ расход охлаждающей среды; ΔеВ ‒ возрастание эксергии охлаждающей среды в холодильниках.
Потребление системы равно
 .
(16.16)
.
(16.16)
Параграф 17. Эксергетический анализ сложных ЭХТС.
ЭХТС представляет собой комплекс взаимосвязанных технологических и энергетических устройств, в котором изменение термодинамического совершенства процессов, протекающих в любом из элементов, приводит к изменению показателей термодинамического совершенства ЭХТС в целом.
В ЭХТС структура потоков эксергии оказывается весьма сложной. Потоки эксергии могут поступать извне одновременно в несколько элементов. Часть потоков эксергии внутри системы оказываются замкнутыми вследствие циркуляции вещества и регенерации теплоты.

Рисунок 17.1 ‒ Обобщенная схема ЭХТС
Для того, чтобы получить зависимость между показателями термодинамического совершенства отдельных элементов и ЭХТС в целом, рассмотрим ее обобщенную схему (рисунок 17.1). Сплошными линиями со стрелками на схеме показаны потоки эксергии.
Среди общего числа N0 элементов системы всегда могут быть выделены N1 головных элементов, через которые в систему поступают потоки эксергии, и N2 концевых элементов, через которые потоки эксергии уходят из ЭХТС. Через систему могут также проходить транзитные потоки эксергии. Суммарный транзитный поток каким-либо образом распределен, с одной стороны, между элементами, через которые эксергия поступает в систему, и, с другой стороны, между элементами, через которые эксергия из системы отводится. В соответствии с определением эксергетического КПД имеем для всей ЭХТС
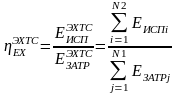 ,
(17.1)
,
(17.1)
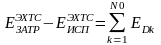 ,
(17.2)
,
(17.2)
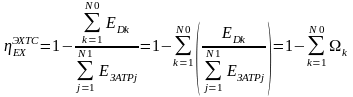 .
(17.3)
.
(17.3)
Потери в k-ом
элементе ЭХТС равны
 .
Тогда
.
Тогда
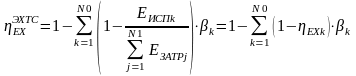 ,
(17.4)
,
(17.4)
где
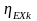 ‒ эксергетический
КПД k-ого
элемента, а
коэффициент
‒ эксергетический
КПД k-ого
элемента, а
коэффициент
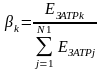 (17.5)
(17.5)
выражает отношение эксергии, затраченной в k-ом элементе, к эксергии, затраченной во всей ЭХТС.
Для
головных элементов
 .
С учетом этого
.
С учетом этого
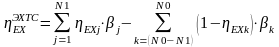 .
(17.6)
.
(17.6)
Таким образом,
влияние эксергетического КПД элемента
на эксергетический КПД системы зависит
от того, какую долю составляет эксергия,
затрачиваемая в данном элементе, по
отношению к общей затраченной в системе
эксергии. Количественно указанное
влияние определяется коэффициентом
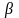 .
.
Для оценки эксергетического КПД ЭХТС, отнесенного к производству конкретного вида продукции, можно воспользоваться формулами (17.5) и (17.6), рассматривая только элементы системы, связанные с производством данного продукта.
В частном случае эксергетический КПД ЭХТС может быть выражен как произведение эксергетических КПД элементов
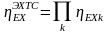 .
(17.7)
.
(17.7)
Однако этой формулой можно пользоваться только при соблюдении следующих условий:
транзит эксергии через систему отсутствует;
вся затраченная эксергия поступает извне только в один из элементов системы;
внутри системы поток эксергии последовательно проходит через все элементы системы от первого до последнего, из которых отводится в виде полезной эксергии.
При соблюдении указанных условий диаграмма Грассмана-Шаргута имеет линейную структуру.
Параграф 18. Особенности эксергетического анализа технологических установок различного принципа действия.
Если целью эксергетического расчета установки является оценка потерь эксергии в ней и выявление вызывающих их причин, то нет необходимости определять все эксергетические потоки, а также результаты их взаимодействия. Методика расчета на этом уровне должна дать возможность определить внешние и внутренние эксергетические потери и места их проявления. Полученная при таком расчете информация позволяет установить распределение и характеристику потерь как для установки в целом, так и для отдельных ее элементов. Также возможно оценить эффективность взаимодействия установки с внешними объектами.
На более высоком уровне эксергетического анализа наряду с потерями в элементах установки определяют потоки эксергии всех видов. В этом случае эффективность работы установки оценивают с помощью относительных характеристик ‒ эксергетического КПД, эксергетической производительности (мощности) и т. д. В этом случае методика расчета должна обеспечивать получение оценок всех происходящих в установке эксергетических превращений, что позволит сопоставить различные технические решения и наметить пути совершенствования исследуемой установки.
Наиболее высокий уровень эксергетического анализа связан с получением функциональных зависимостей, позволяющих исследовать влияние параметров процессов на эксергетические показатели работы данной установки. Методика такого расчета и анализа должна учитывать структурные особенности установки и ее экономические характеристики.
Отметим, что при использовании эксергетических показателей для анализа работы установок на всех уровнях отпадает необходимость подбора процессов или установок в качестве эталона. Использование эксергии позволяет непосредственно определить минимальные энергетические затраты, которые необходимы для реализации процессов в предельном случае, т. е. при их полной обратимости. Тем самым масштаб сравнения задается автоматически.
Особенности методики эксергетического анализа установок различного принципа действия рассмотрим на примерах сушильных установок, так как они включают в себя значительную часть типового тепломассообменного оборудования. Рассмотренные ниже особенности служат основой для эксергетического метода анализа других тепломассообменных установок.
Установки периодического действия. Эксергетический расчет таких установок заключается в определении соответствующих характеристик (потоков и потерь эксергии, эксергетического КПД) для определенных периодов цикла их работы (подготовительного, рабочего, заключительного и т. д.). Следует отметить, что в таких установках интенсивность протекающих в них процессов может изменяться во времени.
В качестве примера рассмотрим сушилку кипящего слоя периодического действия предназначенную для сушки пастообразных продуктов. Она состоит из сушильного шкафа, в который устанавливают сушильную камеру с перфорированным днищем на тележке, в которую загружают пастообразный продукт. После окончания сушки камеру выкатывают для разгрузки, а на ее место устанавливают другую, со следующей порцией продукта. Продукт сушат воздухом, нагреваемым паром, а затем высокотемпературным органическим растворителем с меньшей, чем у пара температурой. Процесс сушки паст из материалов, для которых предназначена установка, состоит из двух периодов: постоянной и падающей скорости.
Для первого периода рассчитывают:
эксергию, отданную сушильным агентом;
затраты эксергии на испарение влаги из высушиваемого материала (полезно затраченная эксергия в первом периоде);
затраты эксергии на нагрев материала;
затраты эксергии на нагрев сушильной камеры;
потери эксергии вследствие смешения паров влаги с сушильным агентом;
потери эксергии вследствие необратимости внутреннего и внешнего теплообмена.
Для второго периода рассчитывают:
эксергию, отданную сушильным агентом;
затраты эксергии на испарение влаги из высушиваемого материала (полезно затраченная эксергия во втором периоде);
затраты эксергии на нагрев материала;
эксергию, отданную сушильной камерой, так как при снижении температуры сушильного агента на входе сушильная камера будет остывать, отдавая избыточное тепло, полученное в первом периоде;
потери эксергии вследствие смешения паров влаги с сушильным агентом;
потери эксергии вследствие необратимости внутреннего и внешнего теплообмена.
Учитывая, что сушильная камера находится внутри установки и омывается сушильным агентом, потери в окружающую среду от нее равны нулю. Потерями через стенки самой сушилки в данном случае можно пренебречь.
На основании проведенных расчетов можно оценить эксергетические затраты на реализацию всего процесса сушки путем суммирования соответствующих статей баланса эксергии по периодам, а также изучить распределение эксергии на разных стадиях процесса.
Установки непрерывного действия. Методика эксергетического расчета таких установок зависит от многих факторов (свойств обрабатываемых материалов, характера протекающих в них тепломассообменных процессов, конструктивных особенностей аппаратов и т. д.). Однако можно выделить общие принципы и приемы, используемые при этом методе анализа таких установок.
В качестве примера рассмотрим конвективную сушильную установку непрерывного действия (рисунок 18.1), в которой в качестве сушильного агента используют воздух, нагреваемый в паровом калорифере.

G ‒ расход вещества; E ‒ расход эксергии; N ‒ мощность
В ‒ воздух; П ‒ пар; М ‒ материал; С. А. ‒ сушильный агент; К ‒ калорифер;
ПР ‒ подсос наружного воздуха; ВЛ ‒ влага; О. С. ‒ окружающая среда

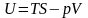

 ;
;
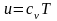
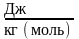
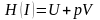
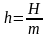 ;
;


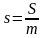 ;
;
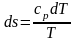

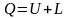
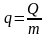 ;
;
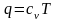
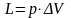
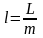 ;
;
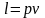

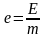 ;
;