Липецкий государственный технический университет

Кафедра Автоматизированных систем управления

Лабораторная работа №3

«Изучение устойчивости систем»

по дисциплине

«Основы теории управления»

Студент

Ключанских А.С

подпись, дата

фамилия, инициалы

Группа

АС-10

Принял

ассистент

Капнин А.В.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2012

1. Цель работы

Изучение устойчивости системы.

2. Задание кафедры

1. Выбрать передаточную функцию в соответствии с вариантом. Проверить устойчивость системы (лекции п. 2.6, 2.7):

• если возможно, сделать вывод об устойчивости системы по передаточной функции;

• построить график переходной функции, сделать предположения об устойчивости;

• построить корневой годограф (Analyze->Root Locus), при необходимости настроить диапазон анализируемых частот (Analyze->Frequency Range), проанализировать нули и полюса (Analyze->Transfer function info), сделать выводы об устойчивости;

• построить годограф системы и сделать вывод об устойчивости на основе модифицированного критерия Михайлова.

2. Замкнуть систему обратной связью;

3. Проанализировать устойчивость полученной системы (одним из способов п. а).

Вариант №11

№	Числитель		Знаменатель
11	-5	7	-1	1	5

3. Экспериментальные результаты и их анализ

1) Передаточная функция системы имеет вид: .

Для устойчивости системы необходимо чтобы корни характеристического уравнения имели отрицательную действительную часть. Характеристическое уравнение имеет вид: . Его корни: , . Данное условие не выполняется, значит, данная система неустойчива.

2) Построим переходную функцию данной системы.

Рисунок 1 – Переходная функция системы

Так как с течением времени переходная функция системы не стремится к какой-либо константе, система неустойчива.

3) Построим корневой годограф по передаточной функции .

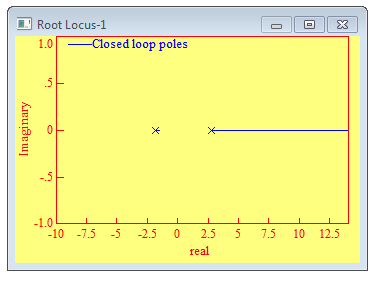
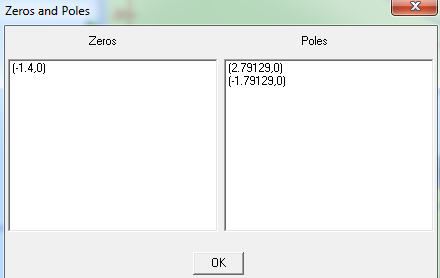
Рисунок 2 – Корневой годограф

Данная система является неустойчивой, тк замкнутая система является устойчивой, если её полюса лежат в левой полуплоскости плоскости корней.

4) Построим годограф системы с передаточной функцией вида: и сделаем вывод об устойчивости на основе модифицированного критерия Михайлова:

Система устойчива тогда и только тогда, если годограф ее характеристического полинома начинается на действительной оси комплексной плоскости и при изменении частоты от нуля до бесконечности последовательно проходит против часовой стрелки n квадрантов, где n – степень характеристического полинома.

В данном случае годограф проходит 1квадрант по часовой стрелке. Порядок характеристического полинома = 2, значит, система неустойчива.

5) Замкнем систему жесткой обратной связью.

Таким образом, передаточная функция замкнутой системы примет вид: .

Построим переходную функцию замкнутой системы.

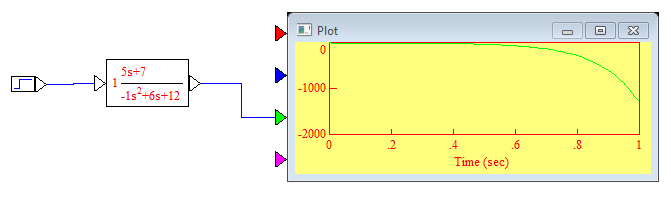
Так как с течением времени переходная функция системы не стремится к какой-либо константе, система неустойчива.

4. Вывод

При выполнении данной лабораторной работы я исследовал заданную систему с помощью различных критериев устойчивости. Все они дали одинаковый результат: система неустойчива.