2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ

Лабораторная работа №3

по дисциплине

«Технология программирования»

на тему:

«Программирование элементарных численных методов»

Студент

Ключанских А.С

подпись, дата

фамилия, инициалы

Группа

АС-10

Принял

Домашнев П.А.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2011

1. Задание кафедры

Написать программу, осуществляющую поиск оптимального значения функции или решение уравнения заданным методом. Интервал поиска (или начальную точку – в зависимости от метода) вводит пользователь. На экране пользователю должен отображаться ход решения, т.е. все промежуточные точки и значения функции в этих точках. Начальные условия (функция, интервал/начальная точка) и ход поиска должны дублироваться в текстовый файл. Имя файла вводит пользователь.

Алгоритм оптимизации	Функция
3 – метод золотого сечения

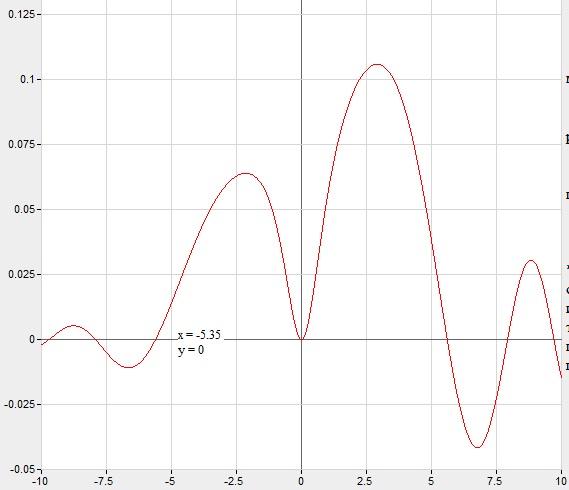
Функция: .

Интервал/начальную точку выбирать в пределах [-10;10].

3. Листинг программы

#include <stdio.h>

#include <conio.h>

#include <math.h>

#include <locale.h>

float func(float x)

{

return sin(x*x/10)*exp(x/10)/(x*x+1);

}

void main(void)

{

char s[15];

FILE *fp;

float a, b, g, h, f1, f2, epsilon; //а,b - исходный интервал, g,h - точки золотого сечения, f1, f2 - значение функции в этих точках

setlocale(LC_ALL,"Russian");

printf("Введите имя файла выходных данных: ");

fp=fopen(gets(s), "w");

printf("Введите интервал: ");

fprintf(fp, "Введите интервал: ");

scanf("%f%f", &a, &b);

fprintf(fp, "%f %f\n", a, b);

printf("Введите точность вычислений: ");

fprintf(fp, "Введите точность вычислений: ");

scanf("%f", &epsilon);

fprintf(fp, "%f\n", epsilon);

g = a+(b-a)*(3-sqrtf(float(5)))/2;

h = a+(b-a)*(sqrtf(float(5))-1)/2;

f1 = func(g);

f2 = func(h);

printf ("Ннаходим минимум на [%f; %f]\n g=%f, f(g)=%f\n h=%f, f(h)=%f", a, b, g, f1, h, f2);

fprintf (fp, "Находим минимум на [%f; %f]\n g=%f, f(g)=%f\n h=%f, f(h)=%f", a, b, g, f1, h, f2);

while (abs(f1-f2) > epsilon)// проверка точности

{

if( f1<=f2 ) // минимум слева от f2

{

b = h;

h = g; //получили интервал от a до h

f2 = f1; //значение функции в новой точке h(которая раньше была точкой g)

g = a+(b-a)*(3-sqrtf(float(5)))/2;

f1 = func(g);

printf("\nМинимум на интервале [%f; %f]\n g=%f h=%f\n f(g)=%f f(h)=%f", a, b, g, h, f1, f2);

fprintf(fp, "\nМинимум на интервале [%f; %f]\n g=%f h=%f\n f(g)=%f f(h)=%f", a, b, g, h, f1, f2);

}

else // справа от f1

{

a = g;

g = h;

f1 = f2;

h = a+(b-a)*(sqrtf(float(5))-1)/2;

f2 = func(h);

printf("\nМинимум на интервале [%f; %f]\n g=%f h=%f\n f(g)=%f f(h)=%f", a, b, g, h, f1, f2);

fprintf(fp, "\nМинимум на интервале [%f; %f]\n g=%f h=%f\n f(g)=%f f(h)=%f", a, b, g, h, f1, f2);

}

}

printf("\nТочка минимума = %f\nМинимум функции = %f\n", (a+b)/2, func((a+b)/2));

fprintf(fp, "\nТочка минимума = %f\nМинимум функции = %f", (a+b)/2, func((a+b)/2));

fclose(fp);

getch();

2. } Контрольный пример

output.txt:

Введите интервал: 5,000000 7,500000

Введите точность вычислений: 0,010000

Находим минимум на [5,000000; 7,500000]

g=5,954915, f(g)=-0,019580

h=6,545085, f(h)=-0,039923

Минимум на интервале [5,954915; 7,500000]

g=6,545085 h=6,909830

f(g)=-0,039923 f(h)=-0,040861

Точка минимума = 6,727458

Минимум функции = -0,041627

График функции: