2

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ

Лабораторная работа №3

по дисциплине

«Технология программирования»

на тему:

«Численные методы»

Студент

подпись, дата

фамилия, инициалы

Группа

Принял

Домашнев П.А.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2010

1. Задание

Написать программу, осуществляющую поиск оптимального значения функции или решение уравнения заданным методом. Интервал поиска (или начальную точку – в зависимости от метода) вводит пользователь. На экране пользователю должен отображаться ход решения, т.е. все промежуточные точки и значения функции в этих точках. Начальные условия (функция, интервал/начальная точка) и ход поиска должны дублироваться в текстовый файл. Имя файла вводит пользователь.

Алгоритм оптимизации	Функция
2 – метод Фибоначчи

Функция: .

Интервал/начальную точку выбирать в пределах [-10;10].

2. Листинг программы

#include <conio.h>

#include <stdio.h>

#include <stdlib.h>

#include <locale.h>

#include <math.h>

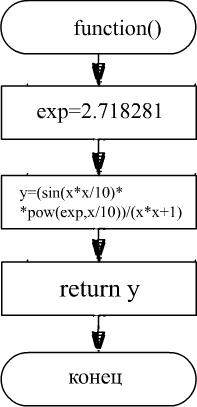
float function(float x)

{

float exp=2.718281, y;

y=(sin(x*x/10)*pow(exp,x/10))/(x*x+1);

return y;

}

void main()

{

setlocale(LC_ALL,"Rus");

float x1, x2, a, b, P1=1.0, P2=1.0;

char name[30];

int i=0,n;

FILE *fp;

printf("Введите имя файла: ");

scanf("%s",&name);

printf("Введите интервал поиска минимума функции [a,b] (a > -10 , b < 10): ");

scanf("%f",&a);

scanf("%f",&b);

printf("Введите количество итераций n: ");

scanf("%f",&n);

fp=fopen(name,"a+");

fprintf(fp,"Начальные условия:\na= %f\nb= %f\ne= %f",a,b,e);

for(i=0;i<n;i++)

{

x1=b-(P1/P2)*(b-a);

x2=a+(P1/P2)*(b-a);

if(function(x1)>function(x2))

a=x1;

else if(function(x1)<function(x2))

b=x2;

P2=P1+P2;

P1=P2-P1;

printf("\nШаг %d: \nТекущий интервал поиска:%f %f\nЗначения в этих точках: %f %f",i,a,b,function(a),function(b));

fprintf(fp,"\nШаг %d: \nТекущий интервал поиска:%f %f\nЗначения в этих точках: %f %f",i,a,b,function(a),function(b));

}

printf("\nl* %f %f\n",a,b);

if(function(a)<function(b))

printf("\nx= %f\ny= %f",a,function(a));

else

printf("\nx= %f\ny= %f",b,function(b));

fclose(fp);

getch();

}

3. Контрольный пример

4.Краткие теоретические сведения.

Метод Фибоначчи используется для нахождения безусловного минимума унимодальных функций f(x).

Функция f(x) называется унимодальной на отрезке [a,b], если

• имеет единственную точку минимума x* на этом отрезке

• f(x) монотонно убывает на [a,x*], возрастает на [x*,b].

Свойства унимодальных функций.

Пусть f(x) унимодальна на [a,b], x,z принадлежат отрезку, x<z, тогда:

1) если f(x)<f(z), то x* принадлежит [a,z];

2) если f(x)>f(z), то x* принадлежит [x,b];

3) если f(x)=f(z), то x* принадлежит [x,z];

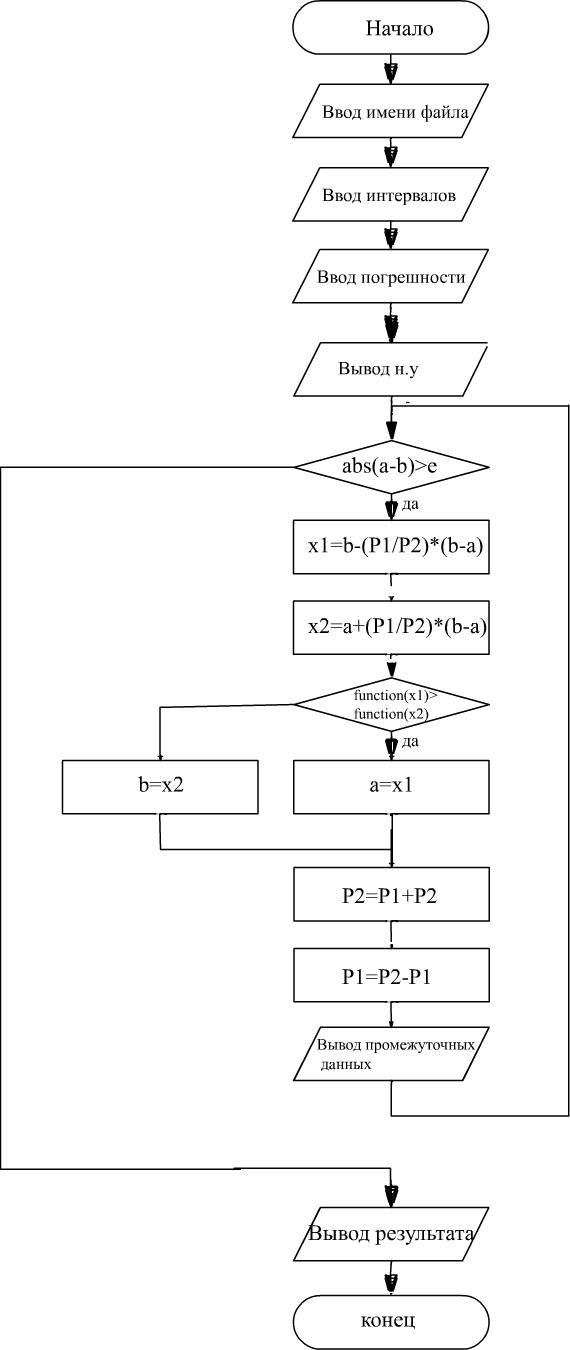
5. Блок-схема

6. Вывод

При выполнении данной лабораторной работы я получил навыки программирования численных методов.

7.Список использованной литературы

1. Шилдт Г. Искусство программирования на C++. БХВ.2005

2. Шилдт Г. C++ Руководство для начинающих. Вильямс.2005

3. Страуструп Б. Язык программирования С++. Специальное издание, 3-изд. Бином.2004