Транспортные сети и задание по алгоритму Флойда / Модуль5_полный поток

5. Транспортные сети. Схемы потоков данных

5.1. Основные определения. Поток в транспортной сети

Транспортной сетью называется орграф D = (V, X) (V={v₁,…,v_n} – множество вершин, Х – множество дуг), для которого выполняются условия:

1. существует одна и только одна вершина v₁, называемая источником, такая, что D ^{– 1}(v₁) = , т.е. ни одна дуга не заходит в v₁;

2. существует одна и только одна вершина v_n, называемая стоком, такая, что D(v_n) = , т.е. из v_n не исходит ни одной дуги;

3. каждой дуге xX поставлено в соответствие целое число с(x)0, называемое пропускной способностью дуги.

Вершины в транспортной сети, отличные от источника и стока, называются промежуточными.

Пример.

Рассмотрим транспортную сеть:

Рис. 5.1. Транспортная сеть D(V, X).

здесь v₁ – источник, v₄ – сток, v₂, v₃ – промежуточные вершины. В скобках при дугах указаны их пропускные способности.

Функция , определенная на множестве Х дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если:

1. для любой дуги xX величина , называемая потоком по дуге х, удовлетворяет условию ;

2. для любой промежуточной вершины v выполняется равенство:

, (5.1)

т.е. сумма потоков по дугам, заходящим в v, равна сумме потоков по дугам, исходящим из v.

Пример.

Для транспортной сети из предыдущего примера (рис. 5.1) определим один из допустимых потоков:

Рис. 5.2. Допустимый поток в транспортной сети D(V, X).

При каждой дуге указана величина потока по ней.

Для промежуточной вершины v₂ получаем:

сумма дуг, заходящих в v₂: ,

сумма дуг, исходящих из v₂: .

Равенство (5.1) выполняется: .

Аналогично для промежуточной вершины v₃:

сумма дуг, заходящих в v₃: ,

сумма дуг, исходящих из v₃: .

Равенство (5.1) выполняется: .

Утверждение 5.1. Для любого допустимого потока в транспортной сети D выполняется равенство:

. (5.2)

Доказательство.

Используя равенство (5.1.), запишем

(5.3)

Для каждой дуги , где , величина входит в левую часть равенства (5.3) лишь один раз и со знаком «+». Аналогично для каждой дуги , где величина входит в левую часть равенства (5.3) лишь один раз и со знаком «–».

С другой стороны, для каждой дуги , где , величина входит в левую часть равенства (5.3) лишь один раз и со знаком «+» (при ) и один раз со знаком «–» (при ), что в сумме дает нулевой вклад в левую часть равенства (5.3).

Доказательство завершено.

Величиной потока в транспортной сети D называется величина , равная сумме потоков по всем дугам, заходящим в v_n, или, что то же самое в силу утверждения, – величина, равная сумме потоков по всем дугам, исходящим из v₁, т.е.

.

Пусть – допустимый поток в транспортной сети D. Дуга называется насыщенной, если поток по ней равен ее пропускной способности, т.е. если .

Поток называется полным, если любой путь в D из v₁ в v_n содержит, по крайней мере, одну насыщенную дугу.

Поток называется максимальным, если его величина принимает максимальное значение по сравнению с другими допустимыми потоками в транспортной сети D.

Из этого следует, что максимальный поток обязательно является полным. Иначе в D существует некоторая простая цепь  из v₁ в v_n, не содержащая насыщенных дуг. Тогда можно увеличить как минимум на единицу потоки по всем дугам цепи , вследствие чего увеличится как минимум на единицу и , что противоречит условию максимального потока. Обратное неверно, т.е. существуют полные потоки, которые не являются максимальными.

5.2. Алгоритм нахождения полного потока в транспортной сети

Рассмотрим один из алгоритмов построения полного потока в транспортной сети D.

1. Полагаем , т.е. начинаем с нулевого потока. Полагаем .

2. Удаляем из орграфа все дуги, являющиеся насыщенными при потоке в транспортной сети D. Полученный орграф снова обозначаем через .

3. Ищем в простой путь  из v₁ в v_n. Если такого пути нет, то – искомый полный поток в транспортной сети D. В противном случае переходим к пункту 4.

4. Увеличиваем поток по каждой дуге x из  на одинаковую величину . В качестве а выбираем такое целочисленное значение, чтобы, по крайней мере, одна дуга из  оказалась насыщенной, а потоки по остальным дугам из  не должны превышать их пропускных способностей. При этом величина потока также увеличивается на а, а сам поток в транспортной сети D остается допустимым. После этого переходим к пункту 2.

Пример.

Дана транспортная сеть D(V, X) (рис. 5.3). Построить полный поток.

Рис. 5.3. Транспортная сеть.

Полагаем =D, , т.е. начинаем с нулевого потока (см. рис. 5.4).

Рис. 5.4. Орграф , , , ₁=v₁v₂v₄v₆.

Насыщенные дуги отсутствуют. Выделим в простой путь ₁=v₁v₂v₄v₆ и увеличим потоки по дугам на а₁ = 3 до насыщения дуги (v₂, v₄) (рис. 5.5)

Рис. 5.5. Поток , .

В результате получим , , содержащий одну насыщенную дугу. Пометим её знаком «~» и удалим из орграфа . Оставшийся граф снова обозначим через (рис. 5.6)

Рис. 5.6. Орграф , ₂=v₁v₂v₃v₄v₆.

Рис. 5.7. Поток , .

Рис. 5.8. Орграф , ₃=v₁v₃v₅v₆.

Рис. 5.9. Поток , .

Рис. 5.10. Орграф , ₄=v₁v₂v₅v₆.

Рис. 5.11. Поток , .

Рис. 5.12. Орграф , ₅.

В полученном графе не существует пути из v₁ в v₆, следовательно, поток является полным (см. рис. 5.11).

5.3. Орграф приращений

Для транспортной сети D и допустимого потока  введем орграф приращений I(D, ). Множество вершин этого орграфа совпадает со множеством вершин транспортной сети. Каждой дуге x = (v, w)X транспортной сети D в орграфе приращений соответствуют две дуги: x = (v, w) – дуга, совпадающая по направлению с дугой транспортной сети, и = (w, v) – дуга, противоположная по направлению дуге транспортной сети. Припишем этим дугам орграфа приращений I(D, ) длину l:

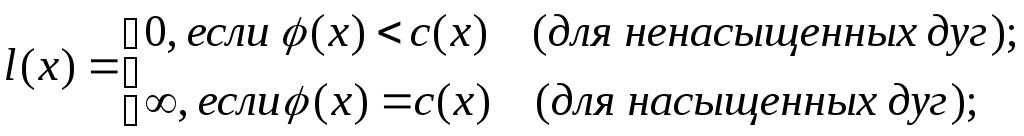(5.4)

(5.5)

В этом случае орграф приращений является нагруженным. При этом видно, что длина любого пути из v₁ в v_n в орграфе I(D, ) равна либо 0, либо .

Пусть  – некоторый простой путь в орграфе I(D, ). Будем говорить, что путь  проходит через дугу x = (v, w)X, если либо x, либо содержится в . При этом, если в  содержится x, то считаем, что направления  и х совпадают, если в  содержится , то считаем, что направления  и х противоположны.

Пример.

Построим орграф приращений для транспортной сети D и потока из предыдущего примера

Рис. 5.13. Орграф приращений I(D, ₄).

6