3.3. Расчет стержневых систем по методу конечных разностей.

Расчет простых балок на изгиб. Пусть некоторая точка оси балки i (рис.3.2,а) соответствует шарнирному опиранию (w_i=0), а точка l находится вне балки (законтурная). Тогда из известного дифуравнения изогнутой оси балки

EI(d²w/dx²)=M_x , (3.3.1)

или в конечных разностях ( λ – шаг сетки):

w_l - 2w_i + w_k = M_i λ²/(EI_i) , (3.3.2)

откуда имеем для законтурной точки l

w_l= - w_k + M_i λ²/(EI_i) , (3.3.3)

где М_i - момент сосредоточенной пары сил, приложенной в т. i.

Рис.3.2.

При жестком защемлении конца балки в т. i прогиб и угол поворота равны нулю (рис.3.2,б):

w_i = 0 ; dw_i/dx = 0 , (3.3.4)

или

(w_l – w_k)/2 = 0 , (3.3.5)

откуда для законтурной точки l :

w_l = w_k . (3.3.6)

При необходимости эти зависимости можно уточнить, удерживая три члена ряда Тейлора:

w_l=w_i+λ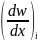 + + 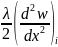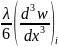. (3.3.7)

Используя приведенные ранее выражения, получим для т. l вне балки

w_l = 3w_k – 0,5w_s . (3.3.8)

Для т. i свободного конца балки (рис.3.2,в) имеем два условия:

(М_х)_i = М_i*; (Q_x)_i = Q_i* , (3.3.9)

где M_i* , Q_i* - заданные усилия в т. i.

Граничные условия (3.3.9) в конечных разностях для свободного конца:

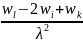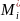= /E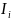 ; (3.3.10)

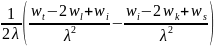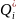= /E , (3.3.10a)

откуда

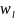= 2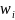 - 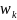+ λ²/EI_i , (3.3.11)

w_l = 4(w_i-w_k)+w_s+2 λ³/EI_i . (3.3.11a)

При = = 0 на свободном конце балки формулы упрощаются.

Балка на упругом (винклеровском) основании. В известное из сопромата дифуравнение изогнутой оси балки

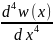+ k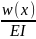 = 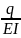, (3.3.12)

где k - коэффициент постели основания (может быть постоянным и переменным);

введем обозначения

EIw = w^* ; k/EI = k^* ,

и перепишем (3.3.12) в виде

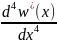+ kw^*(x) = q , (3.3.13)

причем усилия

M_x=d²w^*(x)/dx² ; Q_x=d³w^*(x)/dx³ (3.3.14)

Для любой промежуточной точки i на расстоянии не менее 2λ от концов балки (см. рис.3.3,а), уравнение (3.3.13) примет в конечных разностях вид :

(6+k^*λ⁴)w_i^* - 4(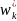 + 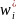)+ +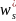 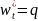_iλ⁴ . (3.3.15)

Рис.3.3.

Для предконтурной точки i на расстоянии λ от конца балки (рис.3.3,б), запишем сначала краевое условие для точки k:

- 2 + =M_kλ² ,

откуда для второй законтурной точки s

=2 - +M_kλ² . (3.3.16)

Тогда для предконтурной точки i разностное уравнение примет вид

(5+k^*λ⁴) - 2 - 4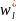 + 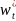=q_iλ⁴ - M_kλ² . (3.3.17)

Для точки i , совпадающей с краем балки (рис.3.3,в), можно , повторяя рассуждения, выразить w_k и w_s через w_i , w_l и w_t на основании двух краевых условий, и тогда разрешающее уравнение в конечных разностях примет вид:

(2+k^*λ⁴) - 4 +2 =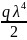 - M_iλ² – 2Q_iλ³ . (3.3.18)

Устойчивость стержней по МКP. Исходя из разрешающего дифуравнения в изгибающих моментах М(х):

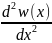+ν²w(x)=0 , (3.3.19)

где критический параметр

= ;

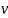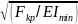в поперечных силах Q(x):

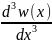+𝜈²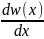 = 0 ; (3.3.20)

в интенсивностях нагрузки q:

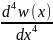+ν² =0; (3.3.21)

запишем эти уравнения в конечных разностях для точки i (рис. 3.4) соответственно в виде:

(ν²λ²– 2)w_i+w_k+w_l=0 , (3.3.22)

(ν²λ² – 2)(w_l-w_k)+w_t – w_s=0 , (3.3.23)

(6 - 2ν²λ²)w_i+(ν²λ² – 4)(w_k+w_l)+w_s+w_t=0 . (3.3.24)

Рис.3.4.

Лекция 4. Метод конечных разностей (ч.2)