МІНІСТЕРСТВО ОСВІТИ та НАУКИ УКРАЇНИ

ОДЕСЬКА ДЕРЖАВНА АКАДЕМІЯ БУДІВНИЦТВА та АРХІТЕКТУРИ

Кафедра будівельної механіки

ЧІСЕЛЬНI МЕТОДИ РОЗРАХУНКУ ПРОСТОРОВИХ

КОНСТРУКЦIЙ

Конспект лекцій для студентів

спеціалізації «Комп ютерна механіка»

Розподіл навантаження

Кредити ECTS - 6

Акад години – 180

Ауд заняття

Разом – 64

Лекції – 28

Практ – 36

Сам роб – 116

Інд завдання

Курсові роботи – 1

РГР,ГР,РР - 2

Іспит – 1

Розподіл кредитів:

1 курс,семестр 1 – 3

Семестр 2 - 3

Баланс самост. роботи

Одеса 2016

ТЕМАТИЧНИЙ ПЛАН

Чисельні методи розрахунку просторових конструкцій

Семестровий модуль 1 (14 год.)

Змістовий модуль 1.Методи розрахунку стержневих систем, пластин,

оболонок та тримірних тіл. Метод скінчених різниць. Варіаційні методи.

Лекція 1. Основні поняття лінійної алгебри.

1.1.Математичні моделі. Вектор, матриця, тензор.Операції з матрицями.

1.2.Визначник та ранг матриці. Системи рівнянь.

1.3.Союзна та зворотня матриці. Трикутні та клітинні (блочні) матриці.

Лекція 2 Основи обчислювательної математики.

2.1.Прямі методи рішення лінійних систем.

2.2.Модифікації метода Гаусса. Порівняння прямих методів.

2.3.Регуляризація погано зумовлених систем.

Лекція 3.Сіточні методи. Метод скінчених різниць (ч.1).

3.1.Методи коллокацій, найменших квадратів, скінчених різниць.

3.2.Інтерполіруючі поліноми та інтерполяційні формули. Похідні.

3.3.Розрахунок стержневих систем за методом скінчених різниць.

Лекція 4.Метод скінчених різниць (ч.2).

4.1.Плоска задача теорії пружностіДиференційні оператори в скінчених різницях.

4.2.Рішення двомірних задач. Розрахунок балок–стінок. Рамна аналогія.

Лекція 5.Ітераційні методи.

5.1.Проста ітерація. Ітерацийні методи із складними операторами.

5.2.Рішення статичних задач теорії пружності.

Лекція 6.Нелінійні задачі теорії пружності.

6.1.Рішення нелінійних задач.

6.2.Швидкозбіжний метод послідовних приближень.

Лекція 7.Варіаційні методи будівельної механіки.

7.1.Класифікація варіаційних методів.

7.2.Метод Ритця та його використання.

7.3.Метод Бубнова – Гальоркіна.

Численные методы расчета пространственных конструкций

Лекция 1.Основные понятия линейной алгебры.

1.1.Математические модели. Вектор, матрица, тензор. Операции с матрицами.

Для каждой конструкции, подлежащей расчету, должна быть выбрана соответствующая физическая модель, причем учесть все особенности геометрии, свойств материала, характера нагружения и т.п. невозможно, да и не нужно. Реальный объект заменяется некоторой физической моделью, обладающей конечным числом особенностей из числа тех, которые присущи исходному объекту. Некоторые свойства, влияние которых незначительно, могут быть проигнорированы (например, мост – перила, столбы электропередач, бордюры тротуаров и т.д.).

Математическая модель включает матризованные входные и выходные данные и математически сформулированный оператор перехода от первых ко вторым, причем одной физической модели может соответствовать несколько математических, так как дополнительные упрощающие предложения могут быть различными (например, для изотропных пластин – гипотеза прямых нормалей; гипотеза прямой линии; гипотеза о равномерности по толщине касательных напряжений и т.п.). Каждая из этих гипотез приводит к своей математической модели. Самой строгой будет модель без каких-либо дополнительных ограничений для зависимостей объемной задачи теории упругости (ТУ). Таким образом, введение дополнительных гипотез сужает область применения данной математической модели, например, гипотеза прямых нормалей Киргхофа допустима лишь для тонких пластинок. Для пластин средней толщины эта гипотеза приводит к заметным погрешностям, и следует обратиться к другим математическим моделям. При дальнейшем увеличении толщины следует отказаться от упрощающих гипотез вовсе, допустимо употребление лишь математической модели на общих зависимостях ТУ.

Подавляющее число задач Механики деформируемого твердого тела (МДТТ) связано с необходимостью решения систем дифуравнений, или обыкновенных, или в частных производных, в общем случае с переменными коэффициентами. Точно проинтегрировать их не всегда возможно – остается путь получения приближенных решений численными методами, которые чаще всего основаны на матричной схематизации процесса вычислений /3, 5/.

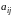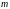Матрицей называется прямоугольная таблица упорядоченной совокупности элементов (чисел или других объектов), содержащая строк и столбцов

/1, 2/:

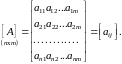(1.1)

Впервые матрицы были использованы английскими математиками А. Кэли и У. Гамильтоном в середине ХІХ в. Такое представление оказалось плодотворным. В разработку общей теории матриц внесли существенный вклад советские математики, в том числе украинские: И.А. Лаппо-Данилевский, А.Н. Крылов, Ф.Р. Гандмахер, а также одессит, долго работавший в ОИСИ чл.-корреспондент АН УССР М.Г. Крейн /4/.

Матрица

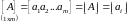(1.2)

называется матрицей – строкой, а матрица

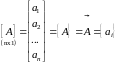(1.3)

называется матрицей – столбцом или вектором.

Матрица размером 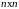называется квадратной матрицей порядка . Квадратная матрица 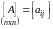называется:

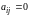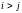а) верхней треугольной, если при , и нижней треугольной при

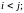
б) диагональной, если при ;

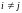в) симметричной, если ;

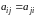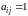г) единичной, если при , при .

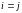Для единичной матрицы порядка принято обозначение:

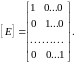(1.4)

Единичная матрица 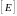играет в матричной алгебре ту же роль, что и единица в обычной алгебре.

Под производной от матрицы 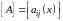по аргументу условно понимают матрицу 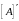, элементами которой являются производные от элементов исходной матрицы по :

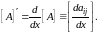(1.5)

Частные производные и интегралы от матриц определяются по аналогии с (1.5).

Операции над матрицами:

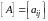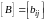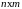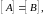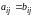а) две матрицы и размером равны друг другу если при всех 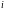и

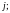
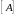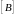б) сумма двух матриц и размером есть матрица 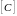размером

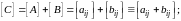(1.6)

в) произведение матрицы размером на скаляр есть матрица размером

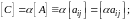(1.7)

г) произведение матриц и имеет место лишь при условии, что число столбцов матрицы первой равно числу строк матрицы второй .

При размерах матрицы и матрицы 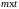их произведение образует матрицу размером

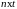
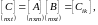(1.8)

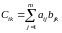где (1.9)

Примечание. Существование произведения не всегда есть существование . Говорят в этом случае, что матрицы некоммутативны.

Обратная матрица. Матрица 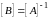называется обратной к квадратной матрице 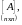если

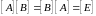(1.10)

Достаточным условием существования обратной матрицы является неособенность матрицы , для которой определитель не равен нулю

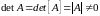
Если 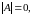то матрица называется особенной, или вырожденной (сингулярной). Произведение двух невырожденных матриц и матрица, обратная невырожденной, являются также невырожденными.

Если в матрице поменять местами строки и столбцы, то получим матрицу 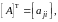которая называется ее транспонированной матрицей.

Операции над произведением нескольких матриц /5/:

а) транспонированная матрица произведения нескольких матриц

(1.11)

б) обратная матрица произведения нескольких невырожденных матриц одного порядка

(1.12)

в) определитель произведения нескольких квадратных матриц одного порядка

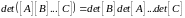(1.13)

Собственными, или характеристическими числами квадратной матрицы будут те значения скалярного параметра 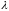, для которого матрица 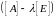становится вырожденной, то есть

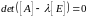(1.14)

Квадратичная форма от переменных 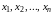есть многочлен

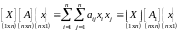(1.15)

где: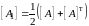 - симметричная часть матрицы .

Квадратичная форма (1.15) будет симметричной и действительной, если - симметрична и действительна.

Действительная и симметричная квадратичная форма (1.15) и соответствующая ей действительная и симметричная матрица называются положительно определенными, отрицательно определенными, неотрицательными, неположительными или неопределенными, если соответственно:

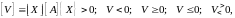то есть если собственные числа матрицы будут все положительны, все отрицательны, все неотрицательны, все неположительны или имеют разные знаки /5/.

1.2.Определитель и ранг матрицы. Системы линейных уравнений.

Определителем (детерминантом) 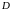квадратной матрицы порядка называется сумма 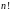членов 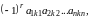каждый из которых соответствует одному из различных упорядоченных множеств 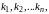полученных попарными перестановками элементов из множества 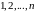/6/:

Фактическое вычисление определителя порядка по его элементам упрощается с введением понятия минора 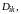который представляет собой определитель 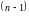-го порядка, если из исходного определителя вычеркнуть -ю строку и 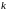-й столбец. Алгебраическое дополнение 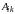элемента 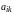есть коэффициент при в разложении определителя , или

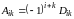(1.16)

Определитель можно выразить через элементы произвольной его строки или столбца и их алгебраические дополнения:

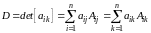(1.17)

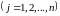(разложение по столбцу или по строке).

Т.о., если матрица – таблица чисел, то определитель – число, записанное в виде таблицы.

Свойства определителя порядка /7/:

1. Определитель не изменится, если его столбцы заменить строками, не меняя их порядка.

2. Переставить местами два столбца (или строки) определителя значит изменить его знак на противоположный (умножить на -1).

3. Определитель, элементы столбца (или строки) которого равны элементам другого столбца (или строки), равен нулю.

4. Общий множитель всех элементов некоторого столбца (или строки) можно выносить за знак определителя.

5. Определитель, у которого все элементы некоторого столбца (строки) равны нулю, равен нулю.

6. Определитель равен сумме произведений элементов 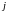-го столбца на их алгебраические дополнения:

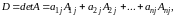
что называется разложением определителя по элементам -го столбца. Определитель может быть разложен по элементам любого своего столбца (или строки) согласно (1.17), что позволяет свести вычисление определителя -го порядка к вычислению определителей -го порядка.

7. Сумма произведений элементов столбца (строки) на алгебраические

дополнения соответствующих элементов другого столбца (строки) равна нулю:

(1.18)

8. Определитель диагональной и треугольной матрицы (как верхней, так и

нижней), равен произведению ее главных диагональных элементов, в частности, определитель единичной матрицы

Ранг матрицы. В прямоугольной матрице размером 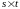можно вычеркнуть несколько строк и несколько столбцов так, чтобы оставшиеся элементы образовали квадратную матрицу порядка , определитель которой является минором данной матрицы. Например, для матрицы (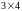 ) путем вычеркивания любого столбца можно получить четыре матрицы порядка 3; вычеркиванием двух столбцов и одной строки можно получить 18 матриц порядка 2; вычеркиванием трех столбцов и двух строк можно получить 12 матриц первого порядка /17/.

Число матриц порядка 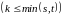, которое можно получить из матрицы размером , равно

,

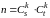где 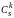и 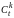есть соответственно число сочетаний из элементов по в каждом из элементов по в каждом. Как известно, число сочетаний из по равно

(1.19)

Для нашего примера 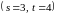, число миноров порядка

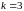
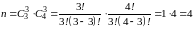
(с учетом, что ).

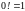Число миноров порядка

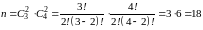
Число миноров порядка

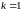
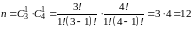
Рангом матрицы называется наибольший порядок минора матрицы, не равного нулю. В нашем случае

Т.о., для определения ранга прямоугольной матрицы надо из ее элементов составить всевозможные квадратные матрицы вычеркиванием строк и столбцов и найти определители этих матриц.

Ранг заданной матрицы равен наивысшему порядку того из этих определителей, который не равен нулю:

а) ранг нулевой матрицы равен нулю

б) ранг диагональной квадратной матрицы равен ее порядку (если ни один из ее диагональных элементов не равен нулю).

Одной из центральных задач вычислительной математики является решение систем линейных уравнений; в общем случае число уравнений может отличаться от числа неизвестных ; в матричной форме /4/:

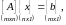(1.20)

где - прямоугольная матрица размером 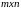, 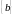- вектор-столбец свободных членов, 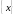- вектор-столбец неизвестных.

Даже если исследуемая система нелинейна, то типичный путь ее исследования и численного анализа лежит через линеаризацию и сводится к решению линеаризованных уравнений типа (1.20).

Если все свободные члены (1.20) 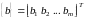равны нулю, то система называется однородной, а если среди них есть хотя бы один 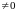, то система называется неоднородной.

Среди уравнений системы (1.20) м.б. линейно-зависимые, которые можно представить как результат сложения других уравнений этой системы, умноженных на некоторые числа; они не содержат никакой дополнительной информации, влияющей на значения искомого вектора . Исключение зависимых уравнений приводит к эквивалентной системе, решение которой совпадает с решением исходной системой (1.20).

Число независимых уравнений определяет ранг системы, а соответственно число независимых строк (или столбцов) матрицы коэффициентов, что является рассмотренным выше рангом матрицы , то есть что хотя бы один ее минор -го порядка отличен от нуля, а все остальные выше r-го порядка, равны нулю.

Таким образом, система уравнений с неизвестными, квадратная матрица которой неособенная (т.е. 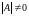), имеет единственное решение 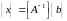и поэтому называется определенной системой -го порядка. Подстановка решения превращает ее в тождество

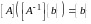, то есть 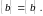(1.21)

Ранг r не только диагональной, но и любой квадратной невырожденной (неособенной) матрицы порядка равен ее порядку

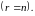
Если среди уравнений с неизвестными имеются линейно зависимые, то - особенная (вырожденная) матрица и ее ранг меньше порядка 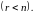Разность

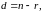(1.22)

называется дефектом матрицы, а саму матрицу называют 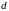-кратно вырожденной (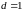 просто вырожденной). После исключения зависимых уравнений получим эквивалентную систему уравнений с неизвестными.

Система уравнений с неизвестными 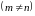может: иметь решение; иметь несколько решений; не иметь решений.

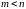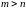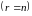Если система имеет хотя бы одно решение, ее называют совместной, а систему, не имеющую решения, называют несовместной. Совместная система при всегда имеет бесконечное множество решений и называется неопределенной. При система является либо несовместной, либо сводится к эквивалентной ей совместной системе, которая может быть определенной , или неопределенной

Применение компьютерной техники позволяет решать системы большого порядка, для этого разработаны высокоэффективные алгоритмы и программы, многие из которых основаны на идее исключения Гаусса, которая используется также для вычисления определителей и обращения матриц.