
- •Задание по курсу «Нейронные сети» Цель задания – овладение практическими навыками построения нейронной сети.
- •Методические указания по выполнению работы Распознавание рукописного текста Определение архитектуры нейронной сети
- •Инициализация нейронной сети.
- •Обучение нейронной сети Алгоритм обратного распространения ошибки
- •Алгоритм наискорейшего спуска
- •Подбор коэффициента обучения
- •Алгоритм обучения нейронной сети
- •Обучение в отсутствие шума
- •Обучение в присутствии шума
- •Повторное обучение в отсутствии шума
- •Эффективность функционирования
- •Моделирование нейронной сети
Обучение нейронной сети Алгоритм обратного распространения ошибки
Алгоритм обратного распространения ошибки представляет стратегию подбора весов многослойной сети с применением градиентных методов оптимизации. Его основу составляет целевая функция, формулируемая в виде квадратичной суммы разностей между физическими и ожидаемыми значениями выходных сигналов
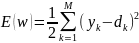 или
или
Формула 1
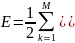
Конкретные компоненты градиента рассчитываются дифференцированием зависимости (1). В первую очередь подбираются веса нейронов выходного слоя. Для выходных весов получаем:
Формула 2
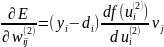
где
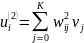 .
.
Если ввести обозначение:
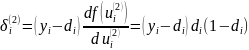 ,
то соответствующий компонент градиента
относительно весов нейронов выходного
слоя можно представить в виде:
,
то соответствующий компонент градиента
относительно весов нейронов выходного
слоя можно представить в виде:
Формула 3
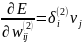
Компоненты градиента относительно нейронов скрытого слоя определяются по тому же принципу:
Формула 4
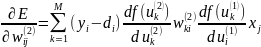
Если ввести обозначение:
Формула 5
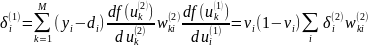
то получим выражение, определяющее компоненты градиента относительно весов нейронов скрытого слоя в виде:
Формула 6
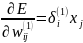
Уточнение вектора весов (обучение) производится по формуле:
Формула 7
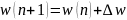
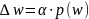
где α – коэффициент обучения, p(w)- направление в многомерном пространстве w. В классическом алгоритме обратного распространения ошибки фактор p(w), учитываемый в выражении «Формула 7», задает направление отрицательного градиента, поэтому:
Формула 8
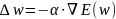
Алгоритм наискорейшего спуска
Если
при разложении целевой функции E(x) в ряд
Тейлора ограничиться ее линейным
приближением, то мы получим алгоритм
наискорейшего спуска. Для выполнения
соотношения
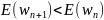 достаточно подобрать
достаточно подобрать
 ,
где
,
где
 .
Условию уменьшения значения целевой
функции отвечает выбор вектора направления
.
Условию уменьшения значения целевой
функции отвечает выбор вектора направления
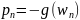 .
.
Подбор коэффициента обучения
Алгоритм
наискорейшего спуска, выбранный для
решения поставленной задачи, позволяет
определить только направление, в котором
уменьшается целевая функция, но не
говорит ничего о величине шага, при
котором эта функция может получить
минимальное значение. После выбора
правильного направления
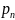 следует определить на нем новую точку
решения
следует определить на нем новую точку
решения
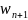 ,
в которой будет выполнено условие
.
Необходимо подобрать такое решение
,
в которой будет выполнено условие
.
Необходимо подобрать такое решение
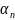 ,
чтобы новое решение
,
чтобы новое решение
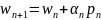 лежало как можно ближе к минимуму целевой
функции в направлении
.
Грамотный подбор коэффициента
оказывает огромное влияние на сходимость
алгоритма оптимизации к минимуму целевой
функции. Чем сильнее величина
отличается от значения, при котором
целевая функция достигает минимума
выбранном направлении, тем больше
количество итераций потребуется для
поиска оптимального решения. Слишком
малое значение
не позволяет минимизировать целевую
функцию за один шаг и вызывает необходимость
повторно двигаться в минимум функции
и фактически заставляет возвращаться
к нему. Один из эффективных методов
подбора коэффициента обучения основан
на его адаптивном подборе с учетом
фактической динамики величины целевой
функции в результате обучения. Стратегия
изменения значения α определяется путем
сравнения суммарной погрешности ε на
i-й итерации с ее предыдущим значением.
Для ускорения процесса обучения следует
стремиться к непрерывному увеличению
α при одновременном контроле прироста
погрешности ε по сравнению с ее значением
на предыдущем шаге. Незначительный рост
этой погрешности считается допустимым.
Если погрешности на (i-1) и i-й итерациях
обозначить соответственно
лежало как можно ближе к минимуму целевой
функции в направлении
.
Грамотный подбор коэффициента
оказывает огромное влияние на сходимость
алгоритма оптимизации к минимуму целевой
функции. Чем сильнее величина
отличается от значения, при котором
целевая функция достигает минимума
выбранном направлении, тем больше
количество итераций потребуется для
поиска оптимального решения. Слишком
малое значение
не позволяет минимизировать целевую
функцию за один шаг и вызывает необходимость
повторно двигаться в минимум функции
и фактически заставляет возвращаться
к нему. Один из эффективных методов
подбора коэффициента обучения основан
на его адаптивном подборе с учетом
фактической динамики величины целевой
функции в результате обучения. Стратегия
изменения значения α определяется путем
сравнения суммарной погрешности ε на
i-й итерации с ее предыдущим значением.
Для ускорения процесса обучения следует
стремиться к непрерывному увеличению
α при одновременном контроле прироста
погрешности ε по сравнению с ее значением
на предыдущем шаге. Незначительный рост
этой погрешности считается допустимым.
Если погрешности на (i-1) и i-й итерациях
обозначить соответственно
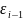 и
и
 ,
а коэффициенты обучения на этих же
итерациях
,
а коэффициенты обучения на этих же
итерациях
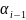 и
и
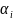 ,
то в случае
,
то в случае
 (
( - коэффициент допустимого прироста
погрешности) значение α должно уменьшаться
в соответствии с формулой:
- коэффициент допустимого прироста
погрешности) значение α должно уменьшаться
в соответствии с формулой:
Формула 9
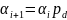
где
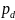 – коэффициент уменьшения α. В противном
случае, когда
– коэффициент уменьшения α. В противном
случае, когда
 ,
,
Формула 10

где
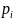 – коэффициент увеличения α.
– коэффициент увеличения α.
Выберем α=0.01, =0.7, =1.05, =1.04.
