
- •Херсон – 2015
- •Методичні рекомендації
- •Завдання з Теоретичної механіки статика
- •Приклад виконання завдання
- •Приклад виконання завдання
- •Задача Кінематика
- •Приклад виконання завдання
- •Завдання дс. Динаміка механічної системи
- •Умови задач завдань дс
- •Задачі завдання дс
- •Приклад виконання завдання
- •Завдання до розділу "Деталі машин і основи проектування"
- •Приклад вирішення
- •Література
Приклад виконання завдання
Задача. Визначити реакції підшипників А і В, а також величину сили P, що тримає вал у рівновазі (рис.1),якщо G=10кH, Q=15кH, M=25кH M, a=0,4M, в=0,24м, α=35, β=30.
Дано: G=10кН Q=15кН M=25кН м а= 0,4м в=0,24м α=
|
Рис.1 |
|
Розв’язання.
У даному випадку розглядається рівновага
вала АВ. Зобразимо його на рис.2 і
прикладемо до нього всі відомі (активні
) сили, включно і пару сил її векторним
моментом
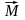 . Оскільки в’язі в точках А і В є нерухомими
циліндричними шарнірами, то реакції їх
відповідно виражаються складовими
. Оскільки в’язі в точках А і В є нерухомими
циліндричними шарнірами, то реакції їх
відповідно виражаються складовими
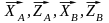 ,
якщо нехтувати тертям вздовж їх спільної
осі АВ. Таким чином маємо зрівноважену
просторову систему сил прикладену до
вільного твердого тіла (рис 2).
,
якщо нехтувати тертям вздовж їх спільної
осі АВ. Таким чином маємо зрівноважену
просторову систему сил прикладену до
вільного твердого тіла (рис 2).
Складаємо рівняння рівноваги цієї довільної просторової системи сил:

Рис. 2
1.
;
 ;
;
2. ; 0 = 0;
3.
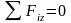 ;
;
 ;
;
4.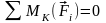 ;
;
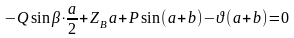 ;
;
5.
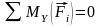 ;
;
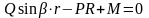 ;
;
6.
 ;
;
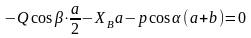 .
.
Рівняння
(5), в яке не входять реакції в’язей,
називається рівнянням
рівноваги твердого тіла
і вданому випадку виражає умову рівноваги
вала АВ. Розв’язавши його відносно сили
Р отримаємо Р=4,79 кН. З інших рівнянь
знаходимо шукані реакції в’язей. З
рівняння (6) знаходимо
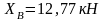 ,а
потім з (1)
,а
потім з (1)
 .
З рівняння (4) знаходимо
.
З рівняння (4) знаходимо
 ,а
потім з (3)
,а
потім з (3)
 .
.
Відповідь: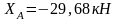 ;
;
;
; ;
;
Р=4,49кН.
;
;
Р=4,49кН.
Рисунок 2

Таблиця 2
№ варіанта |
G, кН |
Q, кН |
Т, кН |
a, см |
b, см |
c, см |
R, см |
r, см |
1 |
6 |
4 |
- |
20 |
15 |
25 |
16 |
4 |
2 |
15 |
6 |
- |
15 |
25 |
20 |
10 |
10 |
3 |
2 |
8 |
- |
10 |
30 |
10 |
- |
- |
4 |
10 |
15 |
- |
15 |
50 |
20 |
15 |
10 |
5 |
8 |
10 |
4 |
10 |
60 |
15 |
20 |
15 |
6 |
3 |
7 |
3 |
20 |
40 |
10 |
20 |
10 |
7 |
4 |
- |
6 |
30 |
20 |
30 |
18 |
6 |
8 |
7 |
12 |
- |
20 |
30 |
15 |
20 |
10 |
9 |
12 |
16 |
4 |
40 |
50 |
20 |
40 |
20 |
10 |
11 |
20 |
5 |
30 |
10 |
30 |
20 |
10 |

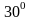 ; β=
; β=
