Лекции / Лекция 12

Лекция 12

Дополняющие величины

В данном методе создается отрицательная корреляция между наблюдениями. Для этого одно наблюдение генерируется с помощью случайного числа r, а другое с помощью его дополняющего партнера (1-r).

В общем случае, когда для проведения одного имитационного опыта используются случайные числа r_1,r₂,...,r_m, то для другого дополнительного опыта используются числа (1-r₁),(1-r₂),...,(1-r_m).

Средний отклик системы при паре наблюдений будет:

,

здесь х₁ и х₂ - отклики в первом и втором опытах соответственно.

Дисперсия оценки:

.

Т.о., дисперсия х уменьшается, если х₁ и х₂ имеют отрицательную корреляцию.

Рассмотрим, почему две указанные последовательности случайных чисел создают отрицательную корреляцию для откликов.

Пусть отклик х зависит от единственного значения единственной случайной входной величины y. Предположим, что х - есть монотонная, например, возрастающая функция от y.

х = g₁(y).

Это значит, что g₁(y₁) > g₁(y₂) ,если y₁>y₂.

Переменная y генерируется случайным числом r с помощью метода обратных функций. Тогда y будет монотонно возрастающей функцией от r.

y = g₂(r)

Это значит, что g₂(r₁) > g₂(r₂) ,если r₁ >r₂.

Следовательно, отклик х - есть монотонно возрастающая функция случайного числа r, т.е.

х = g₃(r)

Это значит, что g₃(r₁) > g₃(r₂) ,если r₁ > r₂.

Даже, если y генерируется не методом обратной функции, все равно обычно y является возрастающей функцией от r. Из монотонного возрастания функции g₃(r) следует, что большие значения x получаются из больших значений r. Но большая величина r приводит к малой дополняющей величине (1-r), т.е. к малому значению отклика x.

Итак, большим значениям отклика x = g₃(r) соответствует малое значение отклика x_a = g₃(1-r). Это значит, что x и x_a отрицательно коррелируют между собой.

В случае, когда на отклик x влияют несколько входных случайных величин , при проведении дополняющего опыта требуется генерировать дополняющие случайные величины для каждой входной величины. Поэтому необходимо, чтобы каждая входная переменная имела свой генератор случайных чисел.

Трудности возникают, когда при проведении имитационных экспериментов количество случайных генерируемых чисел меняется от опыта к опыту.

Здесь встают проблемы синхронизации. Если случайное число r_i генерирует определенное событие, например, прибытие j-го требования в систему, то в дополняющем опыте число (1-r_i) должно генерировать то же самое событие. Такая синхронизация повышает отрицательную корреляцию.

Имеется несколько методов реализации дополняющих случайных величин и случайных чисел.

Метод А

Если машинная память достаточна, то при проведении исходного опыта хранятся все сгенерированные случайные числа. При проведении дополнительного опыта их значения вычитаются из 1.

Метод Б

Если имеется мультипликативный генератор случайных чисел:

,

то дополняющие случайные числа (1-r_i) можно получить, взяв дополняющее начальное значение:

.

Метод В

Если генерируемая входная переменная дискретна, то можно применять процедуру, представленную следующим рисунком:

P P

r _ _ _P₁ _ _

r

_ _ _P₃ _ _ _

P₂

P₂

P₁ P₃

y _i y_i

y₁ y₂ y₃ y₁ y₂ y₃

рис.а рис.б

Здесь мы меняем порядок возможных значений входной переменной на оси абсцисс. Большее значение случайного числа r генерирует большее значение y_i на рис.а. На рис.б ему будет соответствовать малое значение y_i.

Поэтому для генерирования дополняющих значений входной переменной требуется лишь дополнительная таблица, где входная переменная записывается в обратном порядке.

Метод Г

Если входная переменная y имеет симметричное непрерывное распределение со средним значением , то дополняющее значение y_a определяются по формуле:

.

Данный метод может применяться и тогда, когда искомое значение y генерируется не с помощью обратной функции. Статистический анализ имитационных опытов при использовании случайных величин аналогичен стандартному.

Если мы обозначим среднее каждой дополняющей пары как

то

.

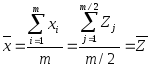Поскольку в каждой переменной Z_j собраны пары дополняющих величин, а каждая пара независима друг от друга, то и все Z_jбудут независимы в совокупности. Поэтому оценка для дисперсии:

.

Доверительные интервалы строятся с помощью критерия Стьюдента с (m/2-1) степенями свободы. Из уменьшения числа степеней свободы значение квантиля распределения Стьюдента возрастает, но это компенсируется уменьшением дисперсии Z по сравнению с x.

По результатам экспериментов понижение дисперсии составляет от 20% до 70%, а в ряде случаев до 500 раз.

Данный метод хорош тем, что удобен в применении и требует мало дополнительного времени на программирование и на счет. При нем также не осложняется статистическая обработка результатов.

Общие случайные числа

В случае, когда моделируются несколько систем (или несколько вариантов одной системы), и нас интересуют различия между системами, мы должны их сравнивать, когда они находятся в равных условиях. Поэтому желательно моделировать системы с одинаковыми начальными условиями. Другое требование: по возможности пользоваться одинаковыми значениями входных переменных.

Например, если у систем N1 и N2 время между поступлениями требований случайное, то обе системы моделируются при одной и той же последовательности случайных чисел.

Статистическое применение общих случайных чисел приводит к корреляции между откликами.

Рассмотрим дисперсию разности между x - откликом системы N1 и y - откликом системы N2. Следовательно, дисперсия оценки уменьшается, если ковариация будет положительной. Такая положительная ковариация достигается, если обе системы реагируют на случайные входы в одном направлении.

Метод общих случайных чисел предполагает, что каждая случайная входная переменная имеет собственную последовательность случайных чисел. При моделировании следующего варианта системы мы будем для генерирования входов брать те же начальные значения для генераторов случайных чисел, что и в предыдущем варианте системы.

Важным вопросом при этом становится синхронизация. Она понимается как использование идентичных случайных чисел при идентичных обстоятельствах в реализации двух процессов.

При моделировании простых систем эта проблема почти не встает. Для сложных систем синхронизация требует дополнительных затрат и решается индивидуально.

Данный метод дает понижение дисперсии от 30% до 95%.

Объем выборки и надежность

Под объемом выборки понимается число наблюдений за поведением одного варианта системы (если проводится факторный эксперимент, то каждый набор значений факторов определяет один вариант системы).

Под надежностью понимается статистическая точность выборочной оценки. Она выражается, например, длиной доверительного интервала и доверительной вероятностью (1-).

При проведении имитированных экспериментов нам приходится решать две задачи:

1. Для заранее установленного объема выборки (числа повторения опытов) найти надежность оценки.

2. При фиксированной желаемой надежности определить требуемый объем выборки.

При определении надежности первой задачей является оценивание дисперсий. На основе этого вычисляется доверительный интервал.

Стандартные методы построения доверительного интервала основаны на предположении независимости и нормальности наблюдений. В имитационной модели предположение о нормальности можно удовлетворить, если откликом одного опыта сделать среднее значение интересующей нас величины в течение одного опыта.

Соответствующая предельная теорема показывает, что среднее даже зависимых наблюдений распределено примерно нормально. Более существенным является предположение о независимости результатов различных имитационных опытов. Проще всего независимые опыты могут быть получены повторениями с помощью различных последовательностей случайных чисел. Но при этом возможно получение смещенных результатов из-за наличия неустановившихся режимов работы модели.

Другой подход - это деление удлиненного опыта на подопыты. Средние значения откликов в каждом подопыте дают нам требуемые данные. В любом случае доверительный интервал для интересующей нас величины строится с помощью распределения Стьюдента со степенями свободы (n -1), где n число наблюдений, или объем выборки:

– квантиль распределения Стьюдента

Кроме оценки среднего (*) можно применять для проверки гипотез о среднем. Если мы хотим проверить гипотезу о том, что Е(х) = _о, то мы смотрим, содержится ли _o в найденном доверительном интервале. Если нет, то гипотезу отвергаем.

При проверке различных средних значений двух моделей мы имеем две нормально распределенные совокупности:

.

Мы имеем независимые наблюдения за моделями:

Существует несколько способов сравнить среднее:

Первый способ

Наблюдения х₁ и х₂ можно спарить, применяя общие случайные числа, тогда х_1i и х_2i будут зависимыми, а сами пары (х_1i,х_2i) останутся независимыми. Тогда мы можем рассматривать величины

.

В этом случае мы возвращаемся к задаче проверки гипотезы о равенстве математического ожидания Е(d)= 0. Эта задача решается с помощью критерия Стьюдента.

Второй способ

Если обе совокупности имеют одинаковую дисперсию:

,

то можно воспользоваться стандартным критерием Стьюдента. Доверительный интервал здесь будет:

где -оценка.

Третий способ

.

В этом случае можно воспользоваться следующим подходом.

Пусть .

В этом случае доверительный интервал:

,

Причем, здесь при вычислении х₂ использованы все n₂ значений опытов со второй моделью, а при определении U_i только n₁ первых значений опытов со второй моделью.

Определение необходимого количества имитационных опытов при заданной надежности происходит следующим образом.

Пусть известно, что закон распределения переменной отклика нормальный с дисперсией ². Если мы хотим, чтобы с вероятностью (1-) оценка среднего отличалась от истинного значения не более чем на С единиц, мы используем уравнение:

, - истинное ср. значение

Поскольку x - среднее n независимых нормально распределенных случайных величин, то можем записать:

,

²(x) – значение дисперсии отклика x при одном имитационном опыте.

Z^/2 – квантиль нормального распределения.

Т.о., можно записать, что:

Это есть искомое число опытов, которые надо провести, чтобы получить оценку с требуемой надежностью. Однако в имитационном моделировании величина ²(x) неизвестна, поэтому вместо нее мы поставим ее оценку S²(x) и используем критерий Стьюдента с (n -1) степенями свободы. Т.е. получим:

Как видно из этого выражения значение n зависит от результатов экспериментов S² (x) и от самого себя .
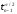